本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为3.7节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

3.7.1

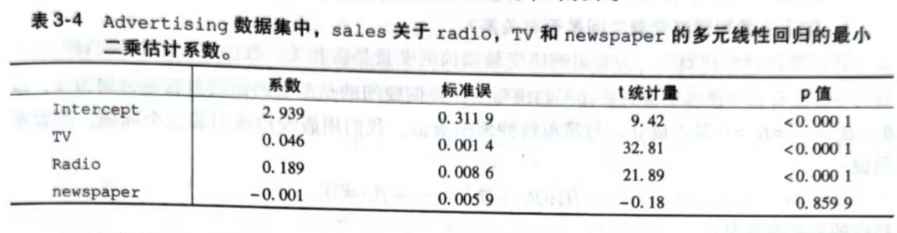
  • 表3-4image-20240920141527253

  • p值对应零假设：

    • TV的零假设：TV广告支出对销售额（sales）没有显著影响（在Radio和newspaper存在时）。（β_{TV}=0）

    • Radio的零假设：Radio广告支出对销售额没有显著影响（在TV和newspaper存在时）。（β_{Radio}=0）

    • newspaper的零假设：newspaper广告支出对销售额没有显著影响（在TV和Radio存在时）。（β_{newspaper}=0）

  • p值得出结论：

    由于TV和Radio的p值远小于0.05，则可以拒绝原假设（零假设）。认为TV/Radio广告支出在另两个变量存在的情况下对销售额（sales）具有显著影响。而newspaper的p值远大于0.05，则接受原假设，认为newspaper广告支出在另两个变量存在的情况下对销售额没有显著影响。

3.7.3

  • (a)

    984264d3fc8c550e5e0a3aab74d56ec

  • (b)

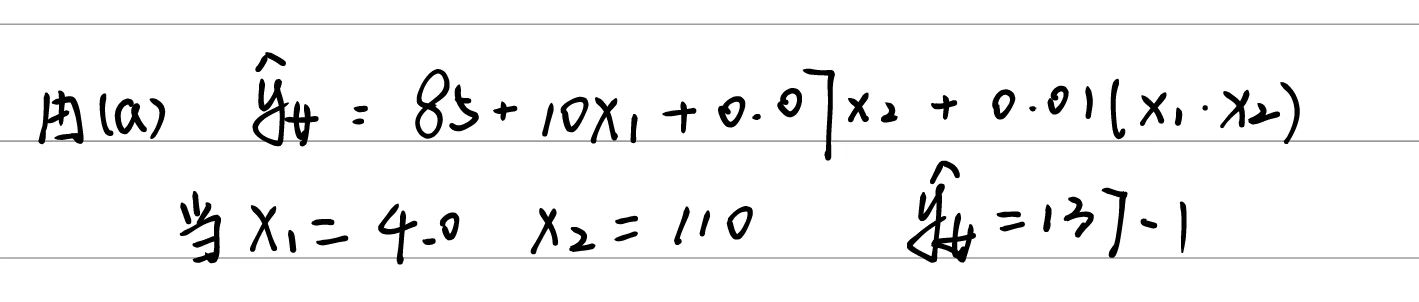
    dbce5a3f9bf94602adcc40560946de2

  • (c)

    错误。交互项的系数不能直接说明两者是否有交互作用。如果需要判断GPA与IQ之间是否存在交互作用，则需要计算对应的p值。若原假设为“两者交互作用不显著”，如果p值小于一个显著性水平（通常为0.05）那么说明原假设不成立，则两者有交互作用。

3.7.4

  • (a)

    线性回归的训练RSS（残差平方和）大于三次回归的训练RSS。原因是三次回归的模型灵活度更高，对训练数据的拟合效果会比线性回归更好，训练RSS会更低。

  • (b)

    线性回归的测试RSS小于三次回归的测试RSS。原因是三次回归模型灵活度高，会出现过拟合的情况。而X和Y恰好满足线性关系，线性回归在测试集上的测试RSS更小。

  • (c)

    线性回归的训练RSS（残差平方和）大于三次回归的训练RSS。原因是三次回归的模型灵活度更高，无论X与Y的线性成都如何，三次回归模型对训练数据的拟合效果都会比线性回归更好，训练RSS会更低。

  • (d)

    根据已知条件无法判断线性回归的测试RSS与三次回归的测试RSS之间的大小。在测试集上，如果数据的真实情况更贴近线性回归，那么线性回归的测试RSS更小。反之如果真实情况更贴近三次回归，则三次回归的测试RSS更小。

二、应用题

3.7.8

  • (a)

    # 8.(a)
library(ISLR)
Auto
lm_mpg_hp = lm(mpg~horsepower, data = Auto)
summary(lm_mpg_hp)
## i.从结果可以看出p值远小于0.05，则可以认为两者有关系
## ii.R^2的值可以看出大约60.59%的mpg变异可以用马力来解释，那么说明两者关系比较强
### iii.从系数为负数得知两者是负相关
predict(lm_mpg_hp, data.frame(horsepower=c(98))) # 预测值是24.46768
predict(lm_mpg_hp, data.frame(horsepower=c(98)), interval="confidence") # 置信区间[23.97308, 24.96108]
# predict(lm_mpg_hp, data.frame(horsepower=c(98)), interval="confidence", level=0.90) 90%置信区间
predict(lm_mpg_hp, data.frame(horsepower=c(98)), interval="prediction") # 预测区间[14.80940, 34.12476]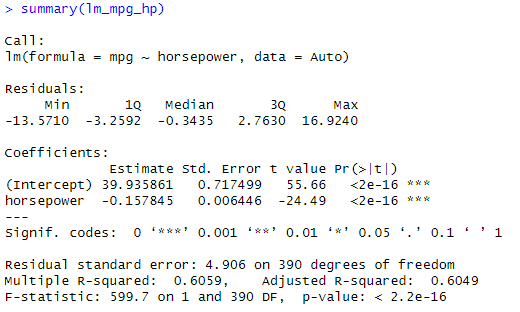

    image-20240920151300371

    image-20240920151723053

  • (b)

    # 8.(b)
plot(Auto$horsepower, Auto$mpg) # 绘制响应变量与预测变量关系图
abline(lm_mpg_hp, col="red") # 最小二乘回归线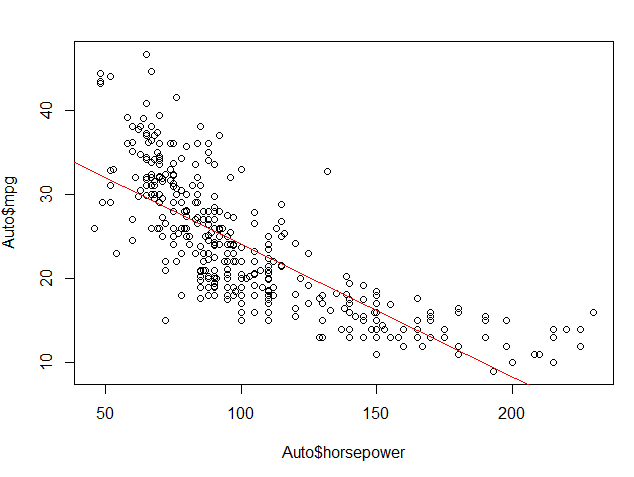

    image-20240920152001086

  • (c)

    # 8.(c)
par(mfrow=c(2,2))
plot(lm_mpg_hp)
# Residuals vs Fitted 残差与拟合值之间的关系。理想情况下，残差应该随机分布在零附近，没有明显的模式。而图中随着拟合值增大残差图呈下凸的曲线，说明二者可能是非线性关系。同时随着拟合值增大，残差范围增大说明可能存在异方差性（误差项方差非恒定）。
# Q-Q Residuals 检查残差是否符合正态分布。如果残差在图中大致沿直线分布，则表明符合正态性。
# Scale-Location 标准化残差的平方根与拟合值。
# Residuals vs Leverage 识别异常值和高杠杆值的点，图中有几个点的杠杆值比较高，残差也比较大，存在异常值。
# 综上得出mpg与horsepower两者可能是非线性关系，使用最小二乘回归拟合效果不好。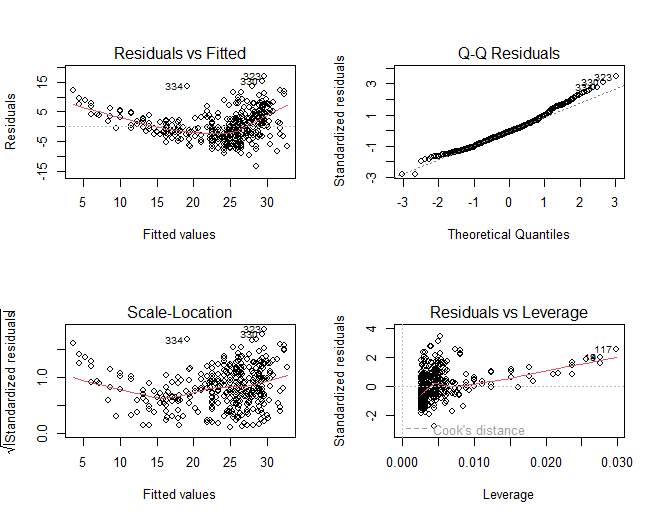

    678376241432

  • 完整代码

    # 8.(a)
library(ISLR)
Auto
lm_mpg_hp = lm(mpg~horsepower, data = Auto)
summary(lm_mpg_hp)
## i.从结果可以看出p值远小于0.05，则可以认为两者有关系
## ii.R^2的值可以看出大约60.59%的mpg变异可以用马力来解释，那么说明两者关系比较强
### iii.从系数为负数得知两者是负相关
predict(lm_mpg_hp, data.frame(horsepower=c(98))) # 预测值是24.46768
predict(lm_mpg_hp, data.frame(horsepower=c(98)), interval="confidence") # 置信区间[23.97308, 24.96108]
predict(lm_mpg_hp, data.frame(horsepower=c(98)), interval="prediction") # 预测区间[14.80940, 34.12476]
​
# 8.(b)
plot(Auto$horsepower, Auto$mpg) # 绘制响应变量与预测变量关系图
abline(lm_mpg_hp, col="red") # 最小二乘回归线
​
# 8.(c)
par(mfrow=c(2,2))
plot(lm_mpg_hp) # 绘制诊断图
# Residuals vs Fitted 残差与拟合值之间的关系。理想情况下，残差应该随机分布在零附近，没有明显的模式。而图中随着拟合值增大残差范围也增大，说明选择的模型不能很好的对数据进行拟合。
# Q-Q Residuals 检查残差是否符合正态分布。如果残差在图中大致沿直线分布，则表明符合正态性。
# Scale-Location 标准化残差的平方根与拟合值。
# Residuals vs Leverage 识别异常值和高杠杆值的点，图中有几个点的刚感知比较高，残差也比较大，存在异常值。
# 综上得出mpg与horsepower两者可能是非线性关系，使用最小二乘回归拟合效果不好。

3.7.11

  • (a)

    # 11.(a)
set.seed(1)
x = rnorm(100) # 生成一个包含100个标准正态分布随机数的向量 x
y = 2*x+rnorm(100) # 生成响应变量 y，它是预测变量 x 的线性函数（2*x），并添加一个独立的标准正态分布噪声项
lm_y_x = lm(y~x+0)
summary(lm_y_x) # 估计系数1.9939，标准差0.1065，t统计量18.73，p值<2e16
## 标准差很小，说明回归系数精确；t统计量较大、p值较小，说明x对y有显著影响。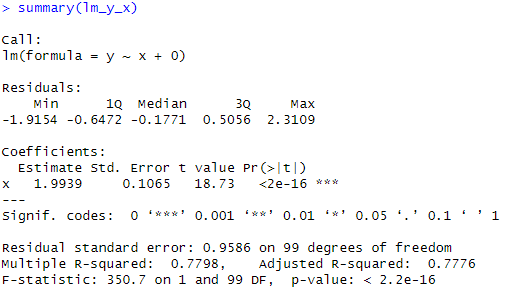

    image-20240920154649868

  • (b)

    # 11.(b)
lm_x_y = lm(x~y+0)
summary(lm_x_y) # 估计系数0.39111，标准差0.02089，t统计量18.73，p值<2e16
## 标准差很小，说明回归系数精确；t统计量较大、p值较小，说明y对x有显著影响（t与p与(a)中相同，说明线性关系本质没有改变）。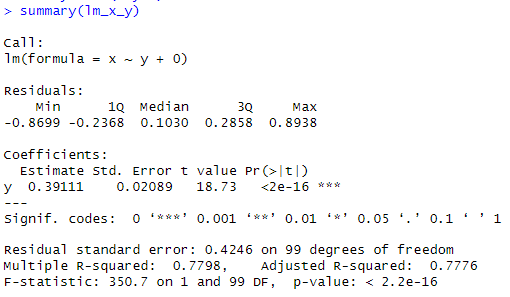

    image-20240920154755442

  • (c)

    # 11.(c)
## (a)与(b)中R方相同，t统计量相同，p值相同，说明线性关系本质没有改变。
## (a)与(b)之间估计系数接近倒数

  • (d)

    # 11.(d)
(sqrt(length(x)-1)*sum(x*y)) / sqrt(sum(x*x)*sum(y*y)-(sum(x*y))^2) # 18.72593

    5ff21a7be2810812a838f22009f135d

  • (e)

    # 11.(e)
(sqrt(length(y)-1)*sum(y*x)) / sqrt(sum(y*y)*sum(x*x)-(sum(y*x))^2) # 18.72953
## (d)中所得t统计量也为18.72953，两者相同

  • (f)

    # 11.(f)
lm_y_x_2 = lm(y~x)
lm_x_y_2 = lm(x~y)
summary(lm_y_x_2) # t统计量18.556
summary(lm_x_y_2) # t统计量18.56 两者基本相同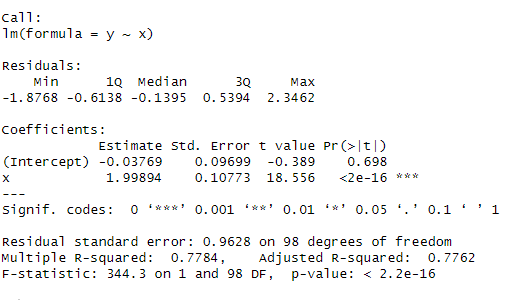

    image-20240920162229364

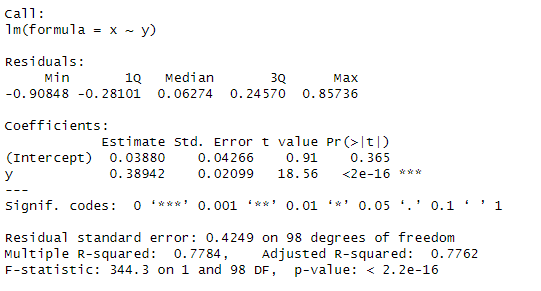
    image-20240920162246023

  • 完整代码

    # 11.(a)
set.seed(1)
x = rnorm(100) # 生成一个包含100个标准正态分布随机数的向量 x
y = 2*x+rnorm(100) # 生成响应变量 y，它是预测变量 x 的线性函数（2*x），并添加一个独立的标准正态分布噪声项
lm_y_x = lm(y~x+0)
summary(lm_y_x) # 估计系数1.9939，标准差0.1065，t统计量18.73，p值<2e16
## 标准差很小，说明回归系数精确；t统计量较大、p值较小，说明x对y有显著影响。

# 11.(b)
lm_x_y = lm(x~y+0)
summary(lm_x_y) # 估计系数0.39111，标准差0.02089，t统计量18.73，p值<2e16
## 标准差很小，说明回归系数精确；t统计量较大、p值较小，说明y对x有显著影响（t与p与(a)中相同，说明线性关系本质没有改变）。

# 11.(c)
## (a)与(b)中R方相同，t统计量相同，p值相同，说明线性关系本质没有改变。
## (a)与(b)之间估计系数接近倒数

# 11.(d)
(sqrt(length(x)-1)*sum(x*y)) / sqrt(sum(x*x)*sum(y*y)-(sum(x*y))^2) # 18.72593

# 11.(e)
(sqrt(length(y)-1)*sum(y*x)) / sqrt(sum(y*y)*sum(x*x)-(sum(y*x))^2) # 18.72953
## (d)中所得t统计量也为18.72953，两者相同

# 11.(f)
lm_y_x_2 = lm(y~x)
lm_x_y_2 = lm(x~y)
summary(lm_y_x_2) # t统计量18.556
summary(lm_x_y_2) # t统计量18.56 两者基本相同

3.7.13

  • (a)

    # 13.(a)
set.seed(1)
x = rnorm(100) # 创建包含100个服从N(0,1)分布的观测
x # 展示x

    image-20240920162804153

  • (b)

    # 13.(b)
eps = rnorm(100, 0, 0.25) # 创建包含100个服从N(0,0.25)分布的观测
eps # 展示eps

    image-20240920162944601

  • (c)

    # 13.(c)
y = -1 + 0.5*x + eps # β0=-1，β1=0.5
length(y) # 长度100

    image-20240920163141421

  • (d)

    # 13.(d)
par(mfrow=c(1,1))
plot(x, y)
## 可以看出y与x成线性正相关的关系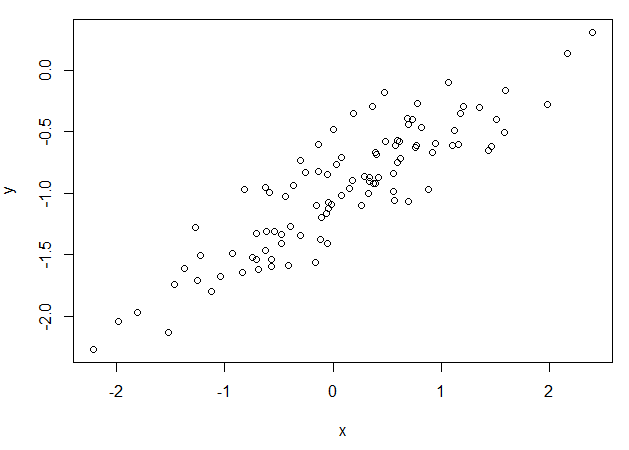

    image-20240920163320225

  • (e)

    # 13.(e)
lm_y_x = lm(y~x)
summary(lm_y_x)
## β0^=-1.00942 β1^=0.49973 与 β0=-1，β1=0.5 几乎相等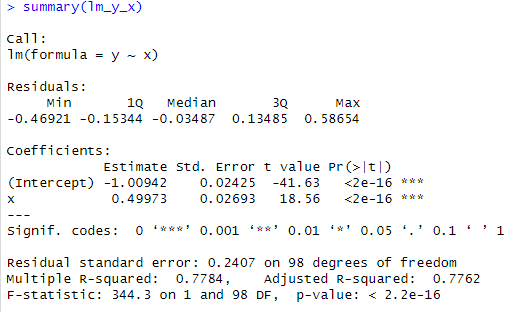

    image-20240920163525586

  • (f)

    # 13.(f)
par(mfrow=c(1,1))
plot(x, y)
abline(-1, 0.5, lwd=5, col="green") # 在图中添加真实的直线，截距为-1，斜率为0.5，线宽为5，颜色为绿色
abline(lm_y_x, lwd=3, col = "red") # 在图中添加回归直线，使用 lm_y_x 模型，线宽为3，颜色为红色
legend("topright", legend=c("真实","回归"), col=c("green", "red"), lwd=3) # 添加图例，位置在右上角，说明绿色线代表“真实”关系，红色线代表“回归”关系，线宽均为3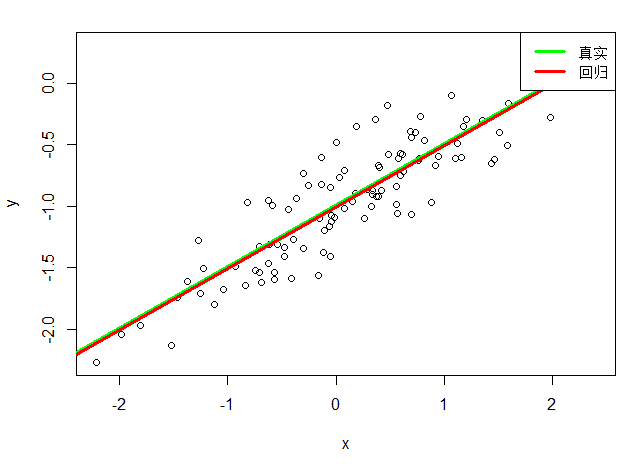

    image-20240920164108505

  • (g)

    # 13.(g)
lm_x2_y = lm(y ~ x+I(x^2)) # 拟合包含 x 和 x^2 的线性模型
summary(lm_x2_y)
## 尽管多项式回归模型的 R-squared 和 Adjusted R-squared 略高，但提升并不显著。二次项 I(x^2) 的 Estimate 为 -0.02973，p 值为 0.164，明显大于 0.05，这表明二次项在统计上不显著。

    image-20240920164559953

  • (h)

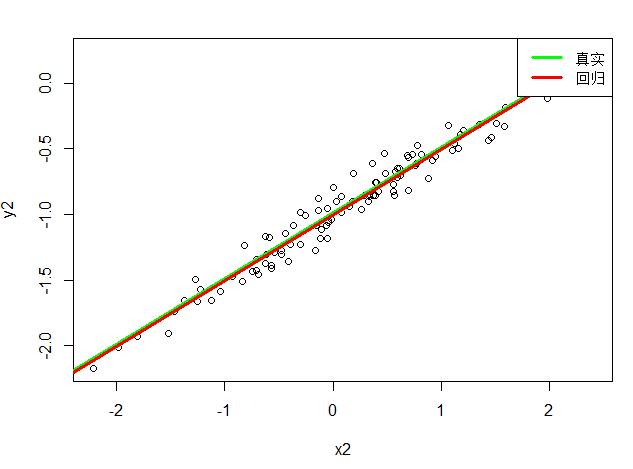
    # 13.(h)
set.seed(1)
x2 = rnorm(100)
eps2 = rnorm(100, 0, 0.1)
y2 = -1 + 0.5*x2 + eps2
lm_y_x_2 = lm(y2~x2)
summary(lm_y_x_2)
par(mfrow=c(1,1))
plot(x2, y2)
abline(-1, 0.5, lwd=5, col="green")
abline(lm_y_x_2, lwd=3, col = "red")
legend("topright", legend=c("真实","回归"), col=c("green", "red"), lwd=3)
## 从R方值的增大和图像可以看出拟合效果更好了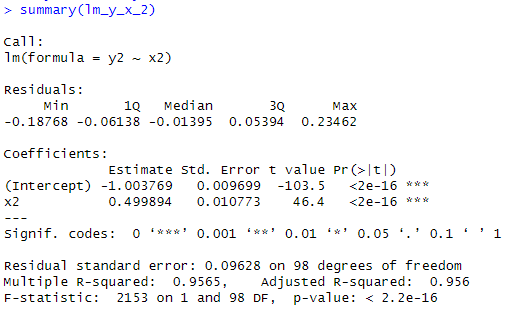

    image-20240920165612260

    image-20240920165624040

  • (i)

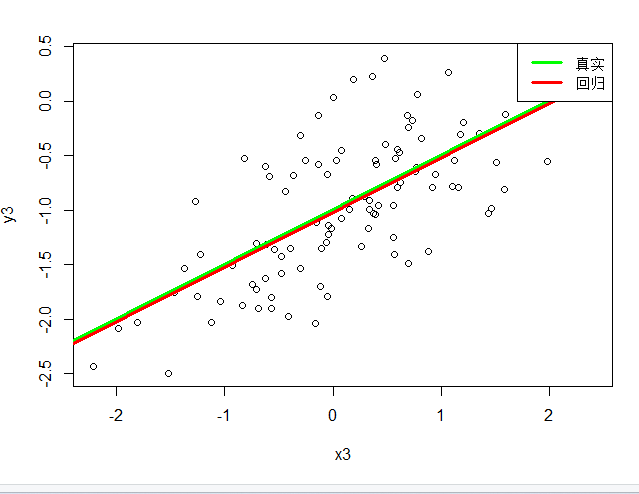
    # 13.(i)
set.seed(1)
x3 = rnorm(100)
eps3 = rnorm(100, 0, 0.5)
y3 = -1 + 0.5*x2 + eps3
lm_y_x_3 = lm(y3~x3)
summary(lm_y_x_3)
par(mfrow=c(1,1))
plot(x3, y3)
abline(-1, 0.5, lwd=5, col="green")
abline(lm_y_x_3, lwd=3, col = "red")
legend("topright", legend=c("真实","回归"), col=c("green", "red"), lwd=3)
## 从R方值的减小和图像可以看出拟合效果更差了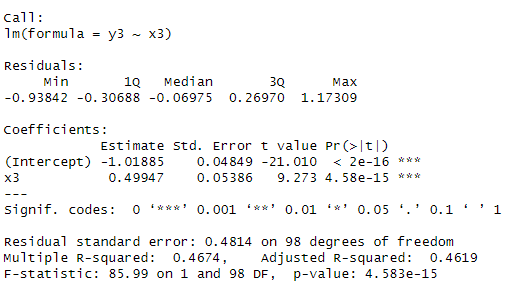

    image-20240920165845774

    image-20240920165857214

  • (j)

    # 13.(j)
confint(lm_y_x)
confint(lm_y_x_2) # 噪声降低，置信区间更小
confint(lm_y_x_3) # 噪声提高，置信区间更大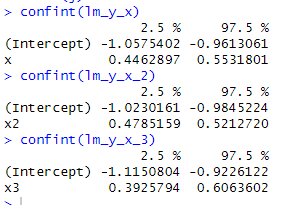

    image-20240920170107455

  • 完整代码

    # 13.(a)
set.seed(1)
x = rnorm(100) # 创建包含100个服从N(0,1)分布的观测
x # 展示x

# 13.(b)
eps = rnorm(100, 0, 0.25) # 创建包含100个服从N(0,0.25)分布的观测
eps # 展示eps

# 13.(c)
y = -1 + 0.5*x + eps # β0=-1，β1=0.5
length(y) # 长度100

# 13.(d)
par(mfrow=c(1,1))
plot(x, y)
## 可以看出y与x成线性正相关的关系

# 13.(e)
lm_y_x = lm(y~x)
summary(lm_y_x)
## β0^=-1.00942 β1^=0.49973 与 β0=-1，β1=0.5 几乎相等

# 13.(f)
par(mfrow=c(1,1))
plot(x, y)
abline(-1, 0.5, lwd=5, col="green") # 在图中添加真实的直线，截距为-1，斜率为0.5，线宽为5，颜色为绿色
abline(lm_y_x, lwd=3, col = "red") # 在图中添加回归直线，使用 lm_y_x 模型，线宽为3，颜色为红色
legend("topright", legend=c("真实","回归"), col=c("green", "red"), lwd=3) # 添加图例，位置在右上角，说明绿色线代表“真实”关系，红色线代表“回归”关系，线宽均为3

# 13.(g)
lm_x2_y = lm(y ~ x+I(x^2)) # 拟合包含 x 和 x^2 的线性模型
summary(lm_x2_y)
## 尽管多项式回归模型的 R-squared 和 Adjusted R-squared 略高，但提升并不显著。二次项 I(x^2) 的 Estimate 为 -0.02973，p 值为 0.164，明显大于 0.05，这表明二次项在统计上不显著。

# 13.(h)
set.seed(1)
x2 = rnorm(100)
eps2 = rnorm(100, 0, 0.1)
y2 = -1 + 0.5*x2 + eps2
lm_y_x_2 = lm(y2~x2)
summary(lm_y_x_2)
par(mfrow=c(1,1))
plot(x2, y2)
abline(-1, 0.5, lwd=5, col="green")
abline(lm_y_x_2, lwd=3, col = "red")
legend("topright", legend=c("真实","回归"), col=c("green", "red"), lwd=3)
## 从R方值的增大和图像可以看出拟合效果更好了

# 13.(i)
set.seed(1)
x3 = rnorm(100)
eps3 = rnorm(100, 0, 0.5)
y3 = -1 + 0.5*x2 + eps3
lm_y_x_3 = lm(y3~x3)
summary(lm_y_x_3)
par(mfrow=c(1,1))
plot(x3, y3)
abline(-1, 0.5, lwd=5, col="green")
abline(lm_y_x_3, lwd=3, col = "red")
legend("topright", legend=c("真实","回归"), col=c("green", "red"), lwd=3)
## 从R方值的减小和图像可以看出拟合效果更差了

# 13.(j)
confint(lm_y_x)
confint(lm_y_x_2) # 噪声降低，置信区间更小
confint(lm_y_x_3) # 噪声提高，置信区间更大