本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为6.8节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

6.8.3

\sum_{i=1}^{n}(y_i-\beta_0-\sum_{j=1}^{p}\beta_jx_{ij}),\sum_{j=1}^{p}|\beta_j|\le s


在该问题中，题目要求最小化残差和并引入了L1正则化约束\sum_{j=1}^{p}|\beta_j| \le s。而传统的Lasso回归要求最小化残差平方和且引入L1正则化约束。但是二者本质上相似，对于约束部分的效果也相同，都是对回归系数的绝对值进行惩罚。

  • (a)

    随着s从0开始增加，对系数的约束也从严格变得宽松。当s=0时，那么要求所有的\beta_j均为0，模型自由度很低。当s足够大时，那么模型也趋近于标准的最小二乘回归。可以看出随着s的增加，模型自由度有所增加，那么在训练集上的拟合效果也就会变好，训练集RSS也会变小。

  • (b)

    随着s的增加，模型自由度逐渐从零模型趋向标准最小二乘回归。期间当s逐渐从0增加到某一特定值的过程中，模型能够使用更多的特征来拟合数据，自由度也趋近于真实情况，此时测试集RSS会随着拟合效果趋于真实情况而减小。当s从特定值再增加的时候，此时自由度的情况开始超过真实情况，出现过拟合的情况，此时模型已经使用了过多的特征，测试集RSS开始增大。综上，测试集RSS最初减小，然后开始增加，图像呈现一个U形。

  • (c)

    当s很小的时候，模型自由度很低，模型使用的特征也很少，所以对数据敏感度很低，方差也比较低。随着s增加，模型自由度提升，对数据敏感度也提高，此时方差就会逐渐变大。所以随着s从0开始增加，方差稳定增长。

  • (d)

    随着s增加，约束放松，模型自由度升高，在测试集上能够更好的拟合数据，能够更好的捕捉数据的模式，偏差稳定减小。

  • (e)

    s的变化会改变对系数的约束，从而影响模型复杂度。而不可约误差是数据本身的固有误差，不会根据模型的改变（包括复杂度的改变）而发生改变。所以随着s增加，不可约误差保持不变。

6.8.4

\sum_{i=1}^{n}(y_i-\beta_0-\sum_{j=1}^{p}\beta_jx_{ij})+\lambda\sum_{j=1}^{p}\beta^2_j


在该问题中，题目要求最小化残差和并引入了L2正则化约束（正则化项\lambda\sum_{j=1}^{p}\beta^2_j）。而传统的岭回归则是要求最小化残差平方和且引入L2正则化约束。但是二者本质上相似，对于约束部分的效果也相同，都是对回归系数的平方值进行惩罚。

  • (a)

    当λ=0时，表示对系数没有约束，那么模型会尽可能拟合数据，拟合效果最好，此时训练RSS最小。随着λ增大，对系数约束增强，惩罚增强，从而模型的复杂度会降低，导致在训练集上拟合效果变差，训练RSS逐渐增大。综上，随着λ从0增加，训练集RSS会稳定增长。

  • (b)

    在λ=0时，没有对系数进行约束，那么模型会使用过多的数据特征，从而导致过拟合，此时测试集RSS比较高。在λ增加之某一个特定值的期间，对系数的约束逐渐增大，模型复杂度逐渐趋近于真实情况，此时测试集RSS会逐渐减小。当λ超过某一特定值，对系数约束过大，模型复杂度开始低于真实情况，此时模型开始过于简单，出现欠拟合情况，导致测试集RSS增大。综上，测试集RSS为最初减小，然后开始增加，图像呈现一个U形。

  • (c)

    在λ=0的时候，对系数没有约束，那么模型会尽可能的拟合数据的特征，此时对训练数据的敏感程度也最高，可能存在过拟合情况，方差最高。在λ逐渐增加的过程中，对系数约束逐渐增大，此时模型对数据敏感程度降低，从而方差也减小。综上，方差随λ增大稳定减小。

  • (d)

    随着λ增大，对系数约束越来越强，模型灵活度越来越低，在训练数据上的拟合效果也越来越差，导致偏差越来越大。所以偏差随λ增大稳定增长。

  • (e)

    λ的变化会改变对系数的约束，从而影响模型复杂度。而不可约误差是数据本身的固有误差，不会根据模型的改变（包括复杂度的改变）而发生改变。所以随着λ增加，不可约误差保持不变。

6.8.5

  • (a)

    7f10386a35ad71c14380eea40fc21ef

  • (b)

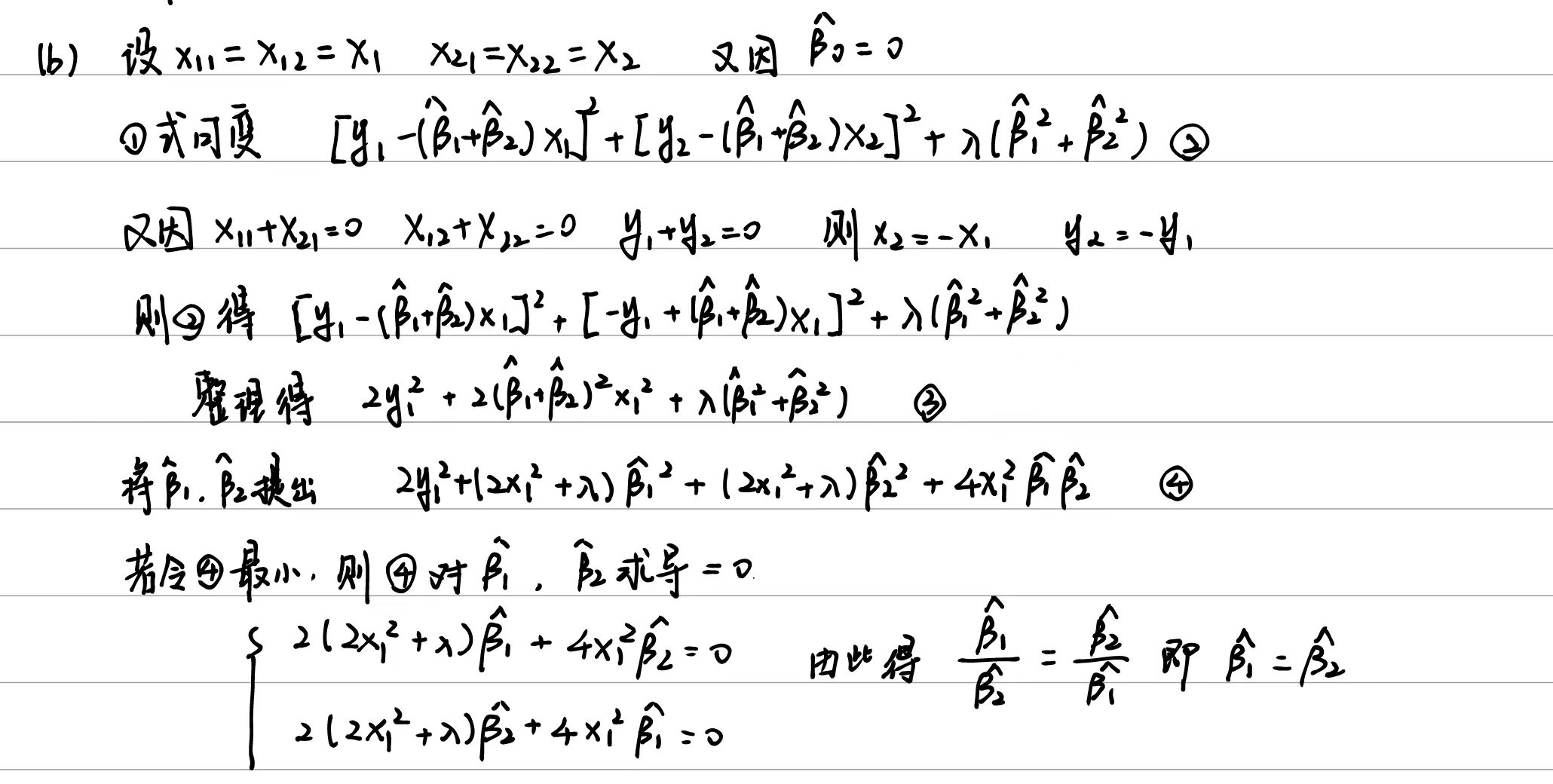
    2fe503cd1a2240b82e8efb9faae805b

  • (c)

    3a15097efd67df08b4bcd5ef651d0e7

  • (d)

    4a985298cab5936864d67785f415bf8

6.8.6

  • (a)

    3596565cd027ffbbfade9509ba9721e

  • (b)

    bd51e4ec9cc8556b05a06ec697953ab

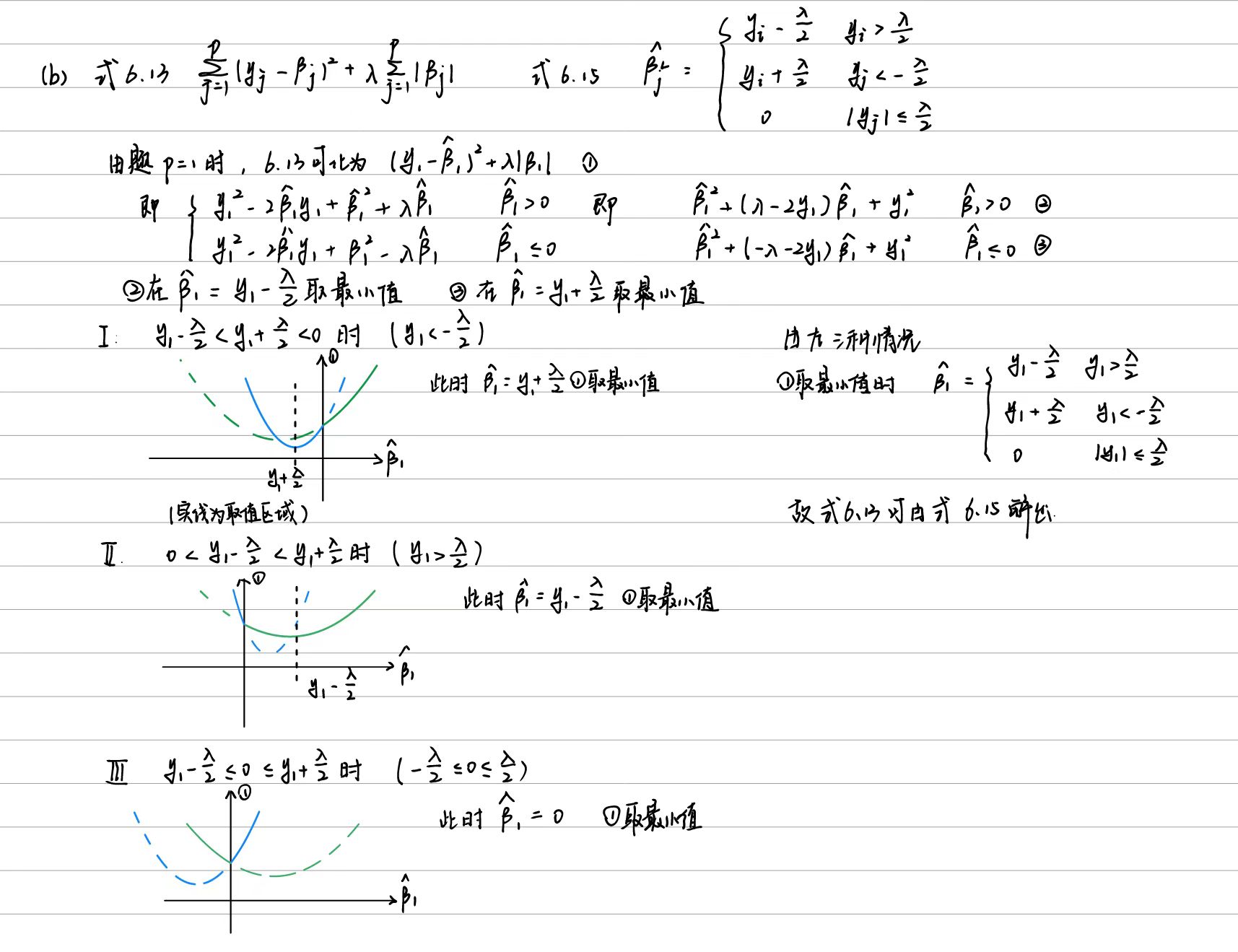
二、应用题

6.8.8

  • (a)

    # 8.(a)
set.seed(1)
X = rnorm(100, mean=0, sd=1) # 默认均值为0，标准差为1
eps = rnorm(100)

    image-20241028151558392

  • (b)

    # 8.(b)
## 设置β0=10，β1=1，β2=5，β3=9
b0 = 10
b1 = 1
b2 = 5
b3 = 9
Y = b0 + b1*X + b2*X^2 + b3*X^3 + eps
par(mfrow = c(1, 1))
plot(X, Y, main="Y=10+X+5X²+9X³")
data.XY = data.frame(x = X, y = Y)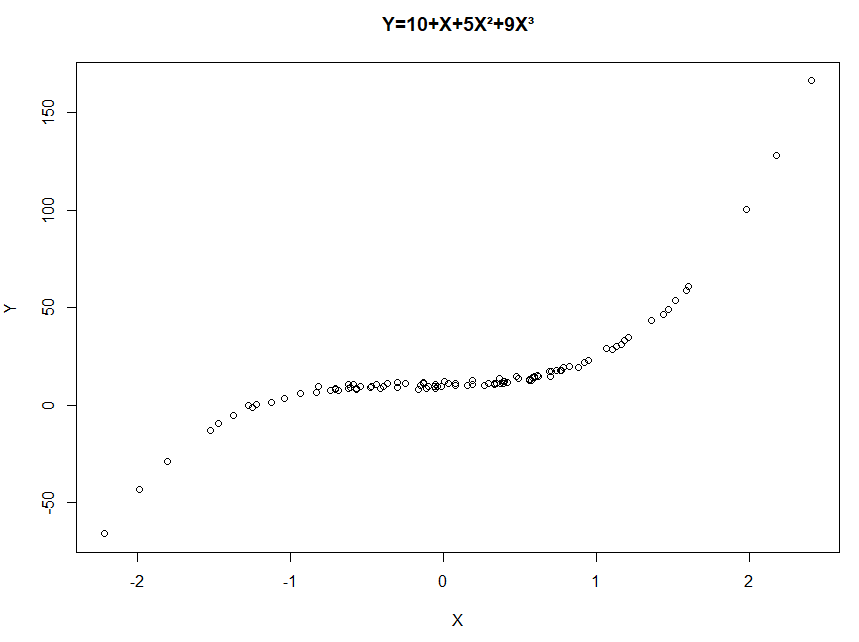

    image-20241028154958761

  • (c)

    # 8.(c)
library(leaps)
model = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY, nvmax=10)
## ploy(x,10,raw=T)生成x到x^10的非正交多项式（非正交：原始多项式，正交：减少多重共线性）
## nvmax最大使用的参数量，即模型最大大小
summary(model)
model.summary = summary(model)
par(mfrow = c(2, 2))
## Cp图
plot(1:length(model.summary$cp), model.summary$cp, xlab = "预测变量数", ylab = "Cp统计量", type = "l") ## type=l绘制线图
points(which.min(model.summary$cp), min(model.summary$cp), col = "red", cex = 2, pch = 20)
### 横轴which.min(model.summary$cp)， 纵轴min(model.summary$cp)， 颜色红色，大小为2，形状为填充
## BIC
plot(1:length(model.summary$bic), model.summary$bic, xlab = "预测变量数", ylab = "BIC", type = "l")
points(which.min(model.summary$bic), min(model.summary$bic), col = "red", cex = 2, pch = 20)
## 调整R²
plot(1:length(model.summary$adjr2), model.summary$adjr2, xlab = "预测变量数", ylab = "调整R²", type = "l")
points(which.max(model.summary$adjr2), max(model.summary$adjr2), col = "red", cex = 2, pch = 20)
## 选择大小为4的模型（虽然实际情况应为3，但是得到结果为4，可能考虑eps项以及随机性）
## 模型包含 常数+一次项+二次项+三次项+五次项
coef(model, 4)
## β0=10.1 β1=1.4 β2=4.8 β3=8.6 β4=0.1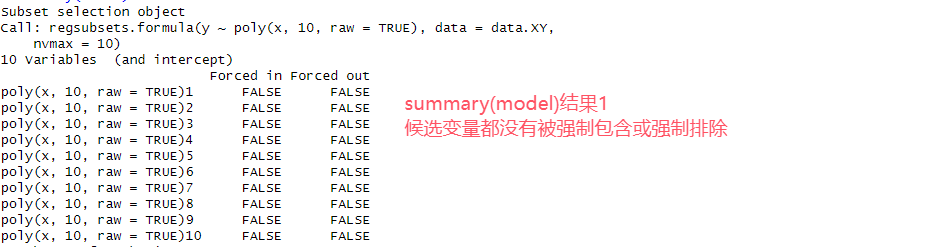

    image-20241028153542700

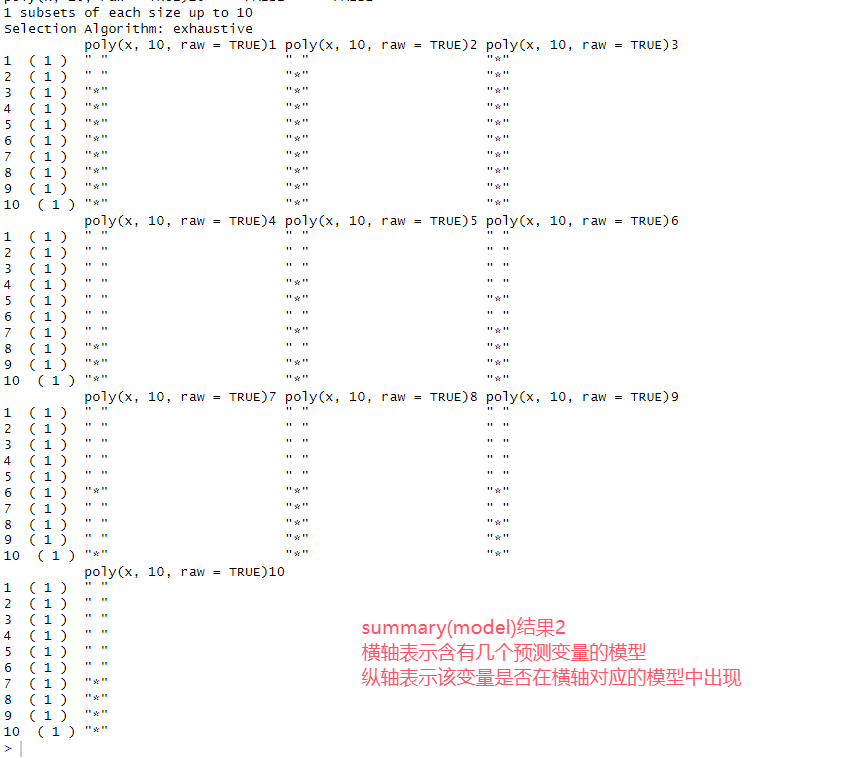
    image-20241028153652654

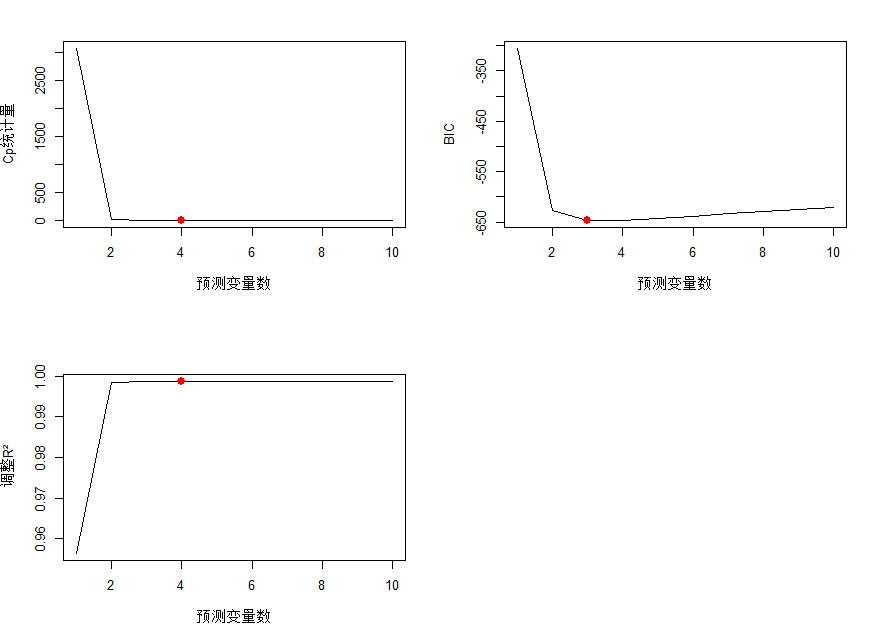
    image-20241028155736939

    image-20241028155909186

    image-20241028160359846

  • (d)

    # 8.(d)
model_forward = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY, nvmax=10, method="forward")
model_forward.summary = summary(model_forward)
print(which.min(model_forward.summary$cp))
print(which.min(model_forward.summary$bic))
print(which.max(model_forward.summary$adjr2))
coef(model_forward, 4)
model_backward = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY, nvmax=10, method="backward")
model_backward.summary = summary(model_backward)
print(which.min(model_backward.summary$cp))
print(which.min(model_backward.summary$bic))
print(which.max(model_backward.summary$adjr2))
coef(model_backward, 4)

    image-20241028161000271

    image-20241028161136672

    image-20241028161311078

  • (e)

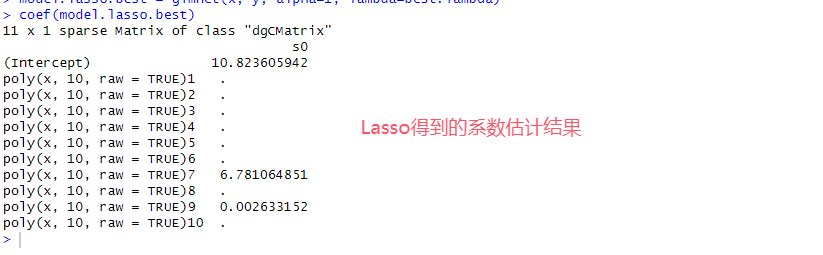
    # 8.(e)
library("glmnet")
x = model.matrix(y ~ poly(x,10,raw=TRUE), data=data.XY)[,-1] ## 创建设计矩阵，并去掉第一列（截距列）
y = data.XY$y
set.seed(1)
model.lasso = cv.glmnet(x, y, alpha=1, nfolds=10) ## alpha=1 Lasso =0 岭 ## nfolds=10折交叉验证
best.lambda = model.lasso$lambda.min
best.lambda ## 0.128264
par(mfrow = c(1, 1))
plot(model.lasso$lambda, model.lasso$cvm, xlab="λ", ylab="MSE", main="Lasso回归交叉验证均方误差-λ", log="x", type ="o")
points(which.max(best.lambda), best.lambda, col = "red", cex = 2, pch = 20)
model.lasso.best = glmnet(x, y, alpha=1, lambda=best.lambda)
coef(model.lasso.best)

    image-20241028163837923

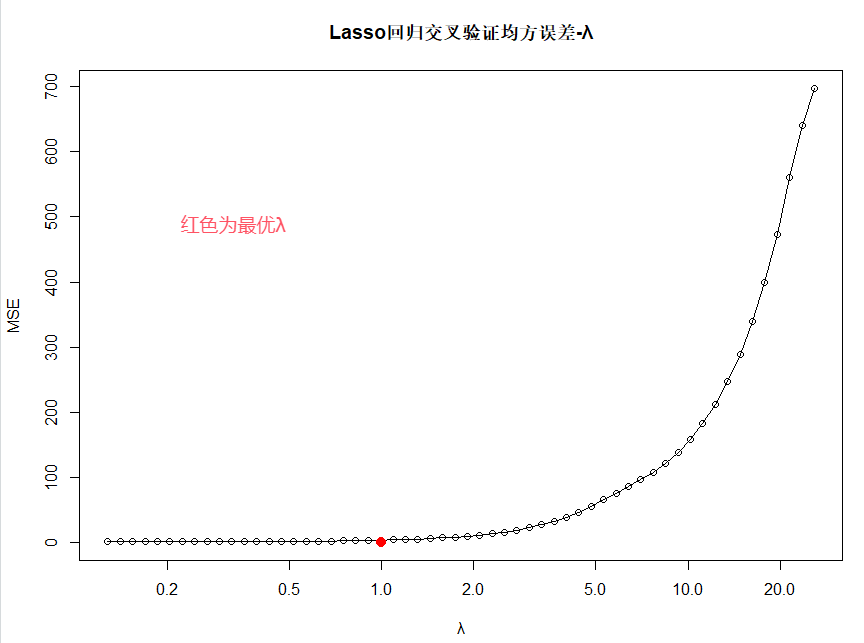
    image-20241028163730839

    image-20241028164249044

  • (f)

    # 8.(f)
Y2 = 10 + 7*X^7 + eps ## β0=10， β7=7
data.XY2 = data.frame(x=X, y=Y2)
model2 = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY2, nvmax=10)
model2.summary = summary(model)
print(which.min(model2.summary$cp))
print(which.min(model2.summary$bic))
print(which.max(model2.summary$adjr2))
coef(model2, 4)
x = model.matrix(y ~ poly(x,10,raw=TRUE), data=data.XY2)[,-1]
y = data.XY2$y
set.seed(1)
model.lasso = cv.glmnet(x, y, alpha=1, nfolds=10)
best.lambda = model.lasso$lambda.min
model.lasso.best = glmnet(x, y, alpha=1, lambda=best.lambda)
coef(model.lasso.best)
## 两种方法在七次项的系数均接近真实值7，而其他项系数均接近0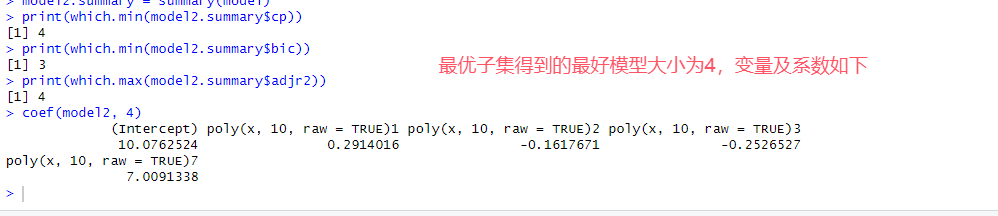

    image-20241028165547395

    image-20241028165720559

  • 完整代码

    # 8.(a)
set.seed(1)
X = rnorm(100, mean=0, sd=1) # 默认均值为0，标准差为1
eps = rnorm(100)
​
# 8.(b)
## 设置β0=10，β1=1，β2=5，β3=9
b0 = 10
b1 = 1
b2 = 5
b3 = 9
Y = b0 + b1*X + b2*X^2 + b3*X^3 + eps
par(mfrow = c(1, 1))
plot(X, Y, main="Y=10+X+5X²+9X³")
data.XY = data.frame(x = X, y = Y)
​
# 8.(c)
library(leaps)
model = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY, nvmax=10)
## ploy(x,10,raw=T)生成x到x^10的非正交多项式（非正交：原始多项式，正交：减少多重共线性）
## nvmax最大使用的参数量，即模型最大大小
summary(model)
model.summary = summary(model)
par(mfrow = c(2, 2))
## Cp图
plot(1:length(model.summary$cp), model.summary$cp, xlab = "预测变量数", ylab = "Cp统计量", type = "l") ## type=l绘制线图
points(which.min(model.summary$cp), min(model.summary$cp), col = "red", cex = 2, pch = 20)
### 横轴which.min(model.summary$cp)， 纵轴min(model.summary$cp)， 颜色红色，大小为2，形状为填充
## BIC
plot(1:length(model.summary$bic), model.summary$bic, xlab = "预测变量数", ylab = "BIC", type = "l")
points(which.min(model.summary$bic), min(model.summary$bic), col = "red", cex = 2, pch = 20)
## 调整R²
plot(1:length(model.summary$adjr2), model.summary$adjr2, xlab = "预测变量数", ylab = "调整R²", type = "l")
points(which.max(model.summary$adjr2), max(model.summary$adjr2), col = "red", cex = 2, pch = 20)
## 选择大小为4的模型（虽然实际情况应为3，但是得到结果为4，可能考虑eps项以及随机性）
## 模型包含 常数+一次项+二次项+三次项+五次项
coef(model, 4)
## β0=10.1 β1=1.4 β2=4.8 β3=8.6 β4=0.1
​
# 8.(d)
model_forward = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY, nvmax=10, method="forward")
model_forward.summary = summary(model_forward)
print(which.min(model_forward.summary$cp))
print(which.min(model_forward.summary$bic))
print(which.max(model_forward.summary$adjr2))
coef(model_forward, 4)
model_backward = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY, nvmax=10, method="backward")
model_backward.summary = summary(model_backward)
print(which.min(model_backward.summary$cp))
print(which.min(model_backward.summary$bic))
print(which.max(model_backward.summary$adjr2))
coef(model_backward, 4)
​
# 8.(e)
library("glmnet")
x = model.matrix(y ~ poly(x,10,raw=TRUE), data=data.XY)[,-1] ## 创建设计矩阵，并去掉第一列（截距列）
y = data.XY$y
set.seed(1)
model.lasso = cv.glmnet(x, y, alpha=1, nfolds=10) ## alpha=1 Lasso =0 岭 ## nfolds=10折交叉验证
best.lambda = model.lasso$lambda.min
best.lambda ## 0.128264
par(mfrow = c(1, 1))
plot(model.lasso$lambda, model.lasso$cvm, xlab="λ", ylab="MSE", main="Lasso回归交叉验证均方误差-λ", log="x", type ="o")
points(which.max(best.lambda), best.lambda, col = "red", cex = 2, pch = 20)
model.lasso.best = glmnet(x, y, alpha=1, lambda=best.lambda)
coef(model.lasso.best)
​
# 8.(f)
Y2 = 10 + 7*X^7 + eps ## β0=10， β7=7
data.XY2 = data.frame(x=X, y=Y2)
model2 = regsubsets(y~poly(x,10,raw=TRUE), data=data.XY2, nvmax=10)
model2.summary = summary(model)
print(which.min(model2.summary$cp))
print(which.min(model2.summary$bic))
print(which.max(model2.summary$adjr2))
coef(model2, 4)
x = model.matrix(y ~ poly(x,10,raw=TRUE), data=data.XY2)[,-1]
y = data.XY2$y
set.seed(1)
model.lasso = cv.glmnet(x, y, alpha=1, nfolds=10)
best.lambda = model.lasso$lambda.min
model.lasso.best = glmnet(x, y, alpha=1, lambda=best.lambda)
coef(model.lasso.best)
## 两种方法在七次项的系数均接近真实值7，而其他项系数均接近0

6.8.9

  • (a)

    # 9.(a)
library(ISLR)
set.seed(1)
n = nrow(College)
train_indices = sample(1:n, size=round(0.7*n)) # 训练集索引，将数据随机抽70%作为训练集
College.train = College[train_indices, ]
College.test = College[-train_indices, ]

    image-20241028213926607

  • (b)

    # 9.(b)
lm_model = lm(Apps ~ ., data = College.train) 
summary(lm_model)
lm_pred = predict(lm_model, College.test) # 使用模型预测测试集
lm_mse = mean((lm_pred - College.test$Apps) ^ 2) # 计算测试均方误差
lm_mse # 1266407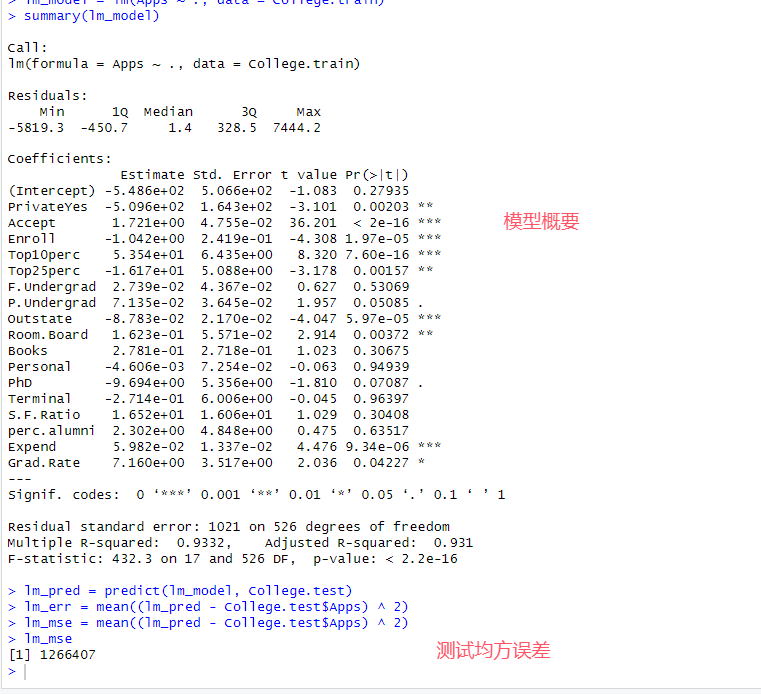

    image-20241028214501246

  • (c)

    # 9.(c)
x_train = model.matrix(Apps ~ ., data = College.train)[, -1]
y_train = College.train$Apps
x_test = model.matrix(Apps ~ ., data = College.test)[, -1]
y_test = College.test$Apps
set.seed(1)
library(glmnet)
lasso_cv = cv.glmnet(x_train, y_train, alpha=0, nfolds=10) ##alpha=0岭回归，nfolds=10十折交叉认证
lasso_bestlambda = lasso.cv$lambda.min
lasso_model = glmnet(x_train, y_train, alpha=0, lambda = lasso.bestlambda)
lasso_pred = predict(lasso_model, x_test)
lasso_mse = mean((lasso_pred - y_test)^2)
lasso_mse # 1126435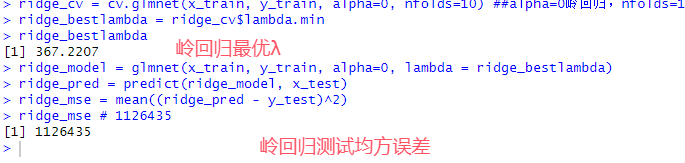

    image-20241028220033860

  • (d)

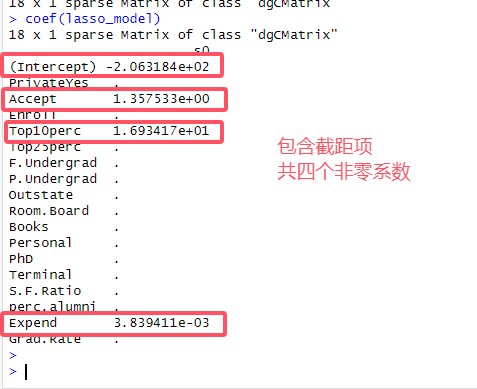
    # 9.(d)
set.seed(1)
lasso_cv = cv.glmnet(x_train, y_train, alpha=1, nfolds=10)
lasso_bestlambda = lasso_cv$lambda.min
lasso.bestlambda
lasso_model = glmnet(x_train, y_train, alpha=1, lambda = lasso.bestlambda)
lasso_pred = predict(lasso_model, x_test)
lasso_mse = mean((lasso_pred - y_test)^2)
lasso_mse # 1346952
coef(lasso_model) # 根据结果共有4个非零系数（包括截距项）

    image-20241028220152527

    image-20241028220606281

  • (e)

    # 9.(e)
library(pls)
set.seed(1)
pcr_cv = pcr(Apps~., data=College.train, scale=TRUE, validation="CV") #拟合PCR模型并进行交叉验证
validationplot(pcr_cv, val.type = "MSEP") # 可视化交叉验证误差，MSEP指定误差类型为均方误差
pcr_bestm = which.min(pcr_cv$validation$PRESS) # 提取使测试残差平方和（PRESS）最小的m
pcr_bestm
pcr_model = pcr(Apps~., data=College.train, scale=TRUE, ncomp=pcr_bestm) # 使用最佳m拟合模型
pcr_pred = predict(pcr_model, College.test, ncomp=pcr_bestm) # 使用PCR模型预测，ncomp设置使用主成分数为bestm
pcr_mse = mean((pcr_pred - College.test$Apps)^2) # 计算均方误差
pcr_mse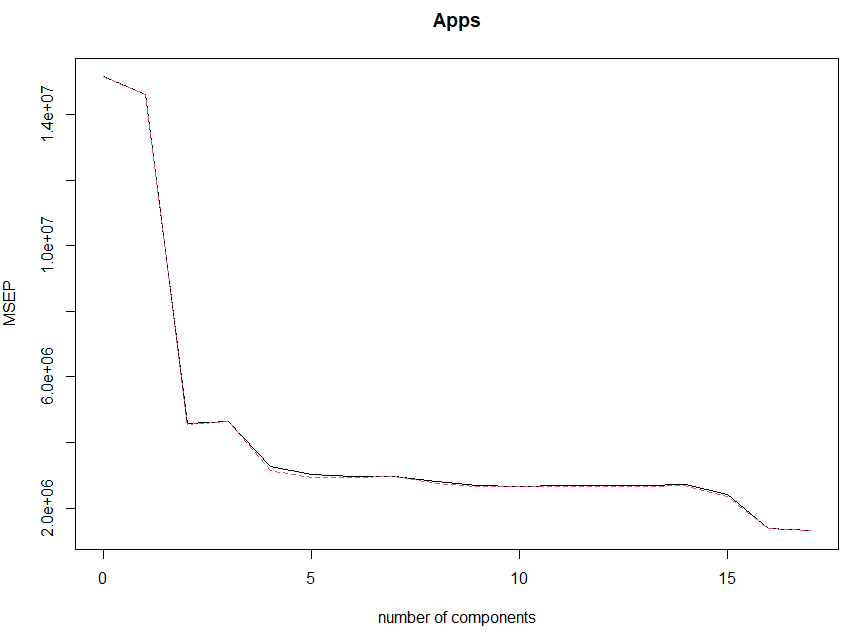

    image-20241028222902141

    image-20241028222403726

  • (f)

    # 9.(f)
set.seed(1)
pls_cv = plsr(Apps~., data=College.train, scale=TRUE, validation="CV")
validationplot(pls_cv, val.type = "MSEP")
pls_bestm = which.min(pls_cv$validation$PRESS)
pls_bestm
pls_model = plsr(Apps~., data=College.train, scale=TRUE, ncomp=pls_bestm)
pls_pred = predict(pls_model, College.test, ncomp=pls_bestm) 
pls_mse = mean((pls_pred - College.test$Apps)^2)
pls_mse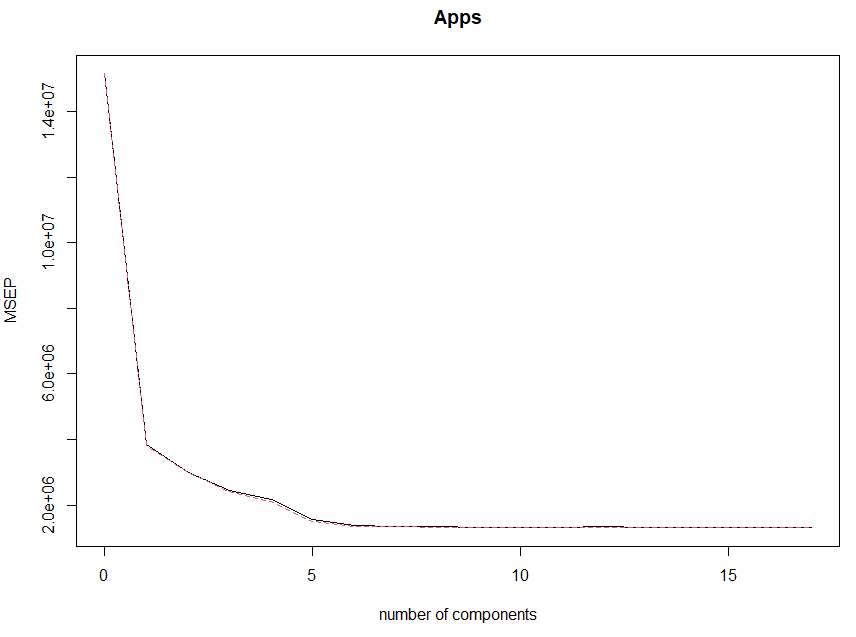

    image-20241028222946202

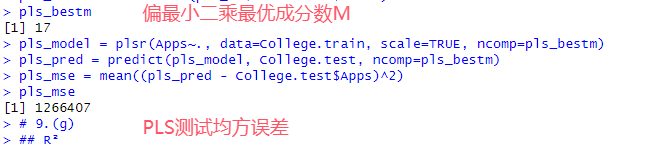
    image-20241028223954066

  • (g)

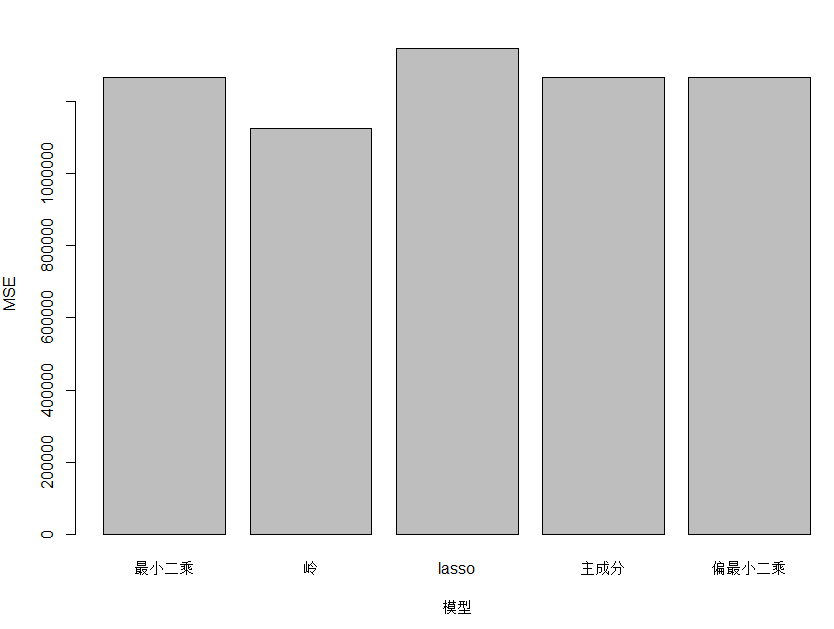
    # 9.(g)
y_mean = mean(y_test)
lm_r2 = 1 - sum((lm_pred - y_test)^2) / sum((y_test - y_mean)^2)
ridge_r2 = 1 - sum((ridge_pred - y_test)^2) / sum((y_test - y_mean)^2)
lasso_r2 = 1 - sum((lasso_pred - y_test)^2) / sum((y_test - y_mean)^2)
pcr_r2 = 1 - sum((pcr_pred - y_test)^2) / sum((y_test - y_mean)^2)
pls_r2 = 1 - sum((pls_pred - y_test)^2) / sum((y_test - y_mean)^2)
models = c("最小二乘", "岭", "lasso", "主成分", "偏最小二乘")
mses = c(lm_mse, ridge_mse, lasso_mse, pcr_mse, pls_mse)
r2s = c(lm_r2, ridge_r2, lasso_r2, pcr_r2, pls_r2)
barplot(r2s, xlab="模型", ylab="R²", names=models)
barplot(mses, xlab="模型", ylab="MSE", names=models)
## 五种模型的测试均方误差相近，并没有特别大的差别
## 通过图像看出岭回归的R²最大，MSE最小，相对来说拟合效果最好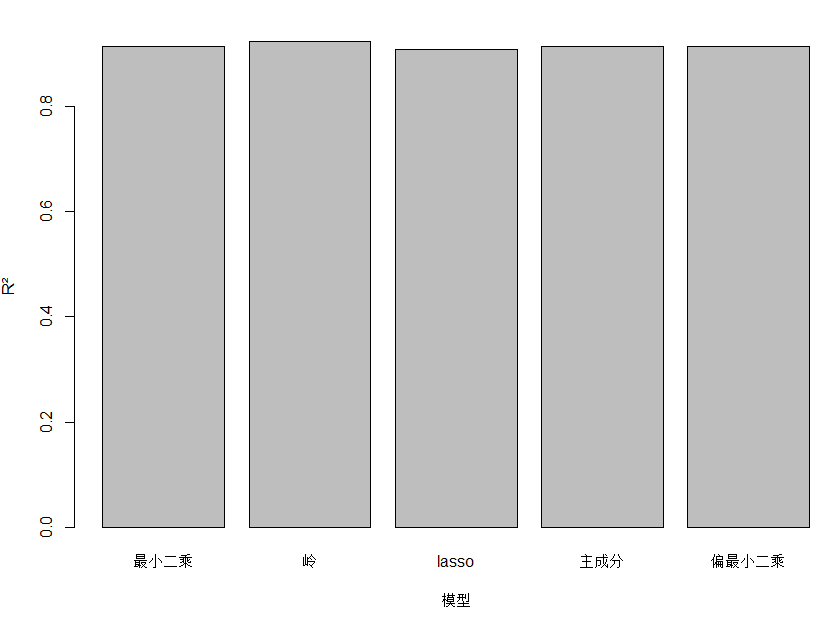

    image-20241028224313158

    image-20241028224330730

  • 完整代码

    # 9.(a)
library(ISLR)
set.seed(1)
n = nrow(College)
train_indices = sample(1:n, size=round(0.7*n)) # 训练集索引，将数据随机抽70%作为训练集
College.train = College[train_indices, ]
College.test = College[-train_indices, ]
​
# 9.(b)
lm_model = lm(Apps ~ ., data = College.train) 
summary(lm_model)
lm_pred = predict(lm_model, College.test) # 使用模型预测测试集
lm_mse = mean((lm_pred - College.test$Apps) ^ 2) # 计算测试均方误差
lm_mse # 1266407
​
# 9.(c)
x_train = model.matrix(Apps ~ ., data = College.train)[, -1]
y_train = College.train$Apps
x_test = model.matrix(Apps ~ ., data = College.test)[, -1]
y_test = College.test$Apps
set.seed(1)
library(glmnet)
ridge_cv = cv.glmnet(x_train, y_train, alpha=0, nfolds=10) ##alpha=0岭回归，nfolds=10十折交叉认证
ridge_bestlambda = ridge_cv$lambda.min
ridge_bestlambda
ridge_model = glmnet(x_train, y_train, alpha=0, lambda = ridge_bestlambda)
ridge_pred = predict(ridge_model, x_test)
ridge_mse = mean((ridge_pred - y_test)^2)
ridge_mse # 1126435
​
# 9.(d)
set.seed(1)
lasso_cv = cv.glmnet(x_train, y_train, alpha=1, nfolds=10)
lasso_bestlambda = lasso_cv$lambda.min
lasso.bestlambda
lasso_model = glmnet(x_train, y_train, alpha=1, lambda = lasso.bestlambda)
lasso_pred = predict(lasso_model, x_test)
lasso_mse = mean((lasso_pred - y_test)^2)
lasso_mse # 1346952
coef(lasso_model) # 根据结果共有4个非零系数（包括截距项）
​
# 9.(e)
library(pls)
set.seed(1)
pcr_cv = pcr(Apps~., data=College.train, scale=TRUE, validation="CV") #拟合PCR模型并进行交叉验证 scale=TRUE表示标准化解释变量
validationplot(pcr_cv, val.type = "MSEP") # 可视化交叉验证误差，MSEP指定误差类型为均方误差
pcr_bestm = which.min(pcr_cv$validation$PRESS) # 提取使测试残差平方和（PRESS）最小的m
pcr_bestm
pcr_model = pcr(Apps~., data=College.train, scale=TRUE, ncomp=pcr_bestm) # 使用最佳m拟合模型
pcr_pred = predict(pcr_model, College.test, ncomp=pcr_bestm) # 使用PCR模型预测，ncomp设置使用主成分数为bestm
pcr_mse = mean((pcr_pred - College.test$Apps)^2) # 计算均方误差
pcr_mse
​
# 9.(f)
set.seed(1)
pls_cv = plsr(Apps~., data=College.train, scale=TRUE, validation="CV")
validationplot(pls_cv, val.type = "MSEP")
pls_bestm = which.min(pls_cv$validation$PRESS)
pls_bestm
pls_model = plsr(Apps~., data=College.train, scale=TRUE, ncomp=pls_bestm)
pls_pred = predict(pls_model, College.test, ncomp=pls_bestm) 
pls_mse = mean((pls_pred - College.test$Apps)^2)
pls_mse
​
# 9.(g)
y_mean = mean(y_test)
lm_r2 = 1 - sum((lm_pred - y_test)^2) / sum((y_test - y_mean)^2)
ridge_r2 = 1 - sum((ridge_pred - y_test)^2) / sum((y_test - y_mean)^2)
lasso_r2 = 1 - sum((lasso_pred - y_test)^2) / sum((y_test - y_mean)^2)
pcr_r2 = 1 - sum((pcr_pred - y_test)^2) / sum((y_test - y_mean)^2)
pls_r2 = 1 - sum((pls_pred - y_test)^2) / sum((y_test - y_mean)^2)
models = c("最小二乘", "岭", "lasso", "主成分", "偏最小二乘")
mses = c(lm_mse, ridge_mse, lasso_mse, pcr_mse, pls_mse)
r2s = c(lm_r2, ridge_r2, lasso_r2, pcr_r2, pls_r2)
barplot(r2s, xlab="模型", ylab="R²", names=models)
barplot(mses, xlab="模型", ylab="MSE", names=models)
## 五种模型的测试均方误差相近，并没有特别大的差别
## 通过图像看出岭回归的R²最大，MSE最小，相对来说拟合效果最好

6.8.10

  • (a)

    # 10.(a)
set.seed(1)
n = 1000 # 观测数
p = 20 # 特征数
X = matrix(rnorm(n*p), nrow = n, ncol = p)
eps = rnorm(n, mean=0, sd=0.3) # 生成标准差为0.3，均值为0的误差项
beta = sample(-10:10, 20) # 生成20个beta，取值在[-10,10]
beta[3] = 0
beta[7] = 0
beta[11] = 0
beta[15] = 0
beta[19] = 0
Y = X %*% beta + eps  # %*%为矩阵乘法运算符
data_XY = data.frame(X, Y) # 组合数据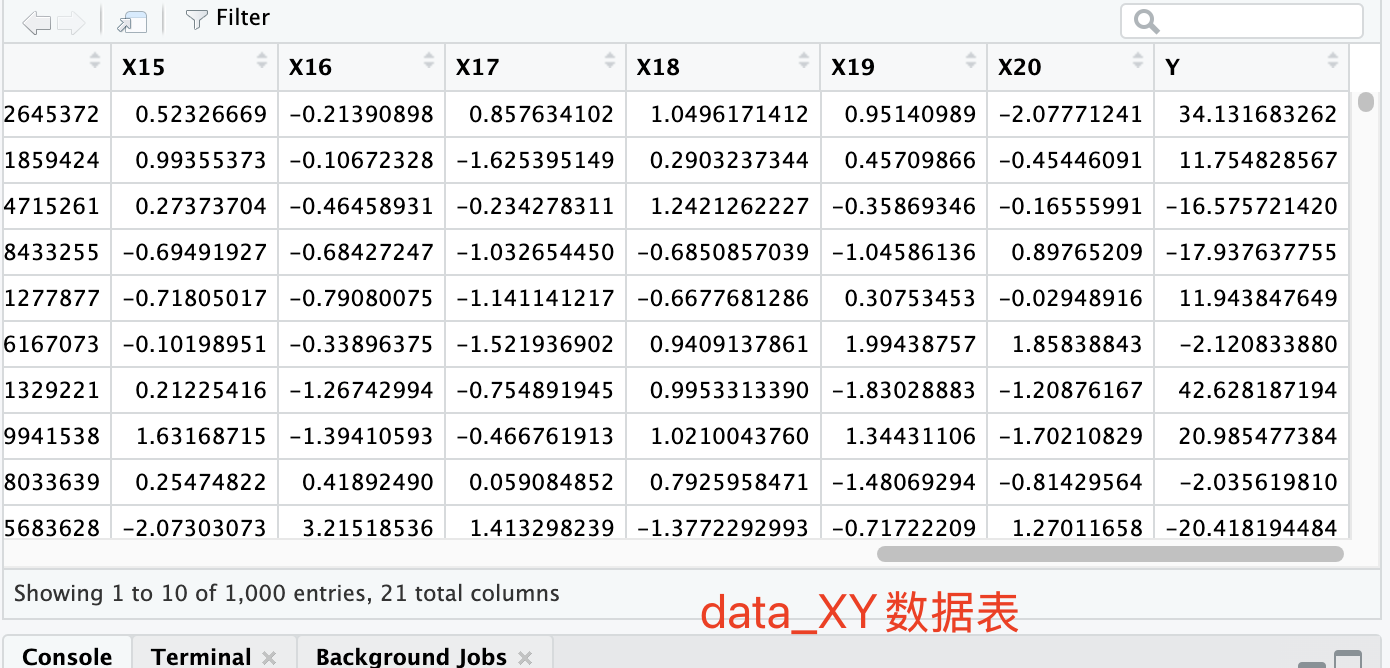

    image-20241029130348360

  • (b)

    # 10.(b)
set.seed(1)
train_indices = sample(1:n, size = 100)
data_train = data_XY[train_indices, ]
data_test = data_XY[-train_indices, ]

    image-20241029130942518

  • (c)

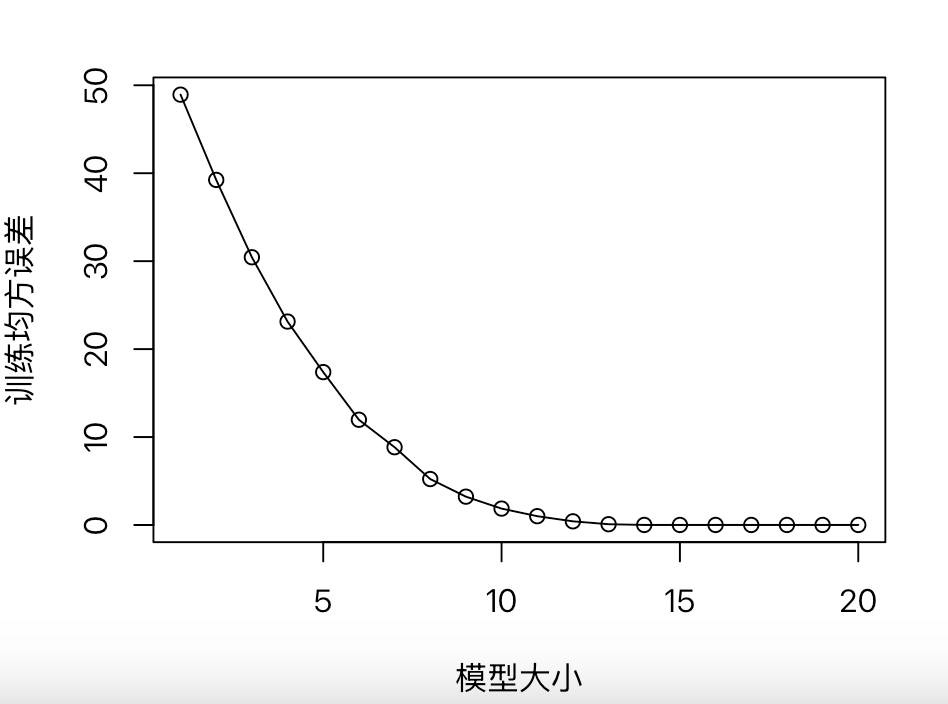
    # 10.(c)
library(leaps)
set.seed(1)
model = regsubsets(Y~., data=data_train, nvmax=20) # 使用最优子集法，最大预测变量数20
model.summary = summary(model)
model.rss = model.summary$rss
model.mse = model.rss / n # 均方误差=RSS/样本数
print(model.mse)
plot(1:20, model.mse, xlab="模型大小", ylab="训练均方误差", pch=1, type="o")

    image-20241029131909535

    image-20241029132700740

  • (d)

    # 10.(d)
library(HH)
test.mse = numeric(p) # 生成一个初始化为0、包含20元素的向量
for(i in 1:20){
  test.model = lm.regsubsets(model, i) # 从regsubsets对象中提取指定大小的模型
  test.pred = predict(test.model, data_test)
  test.mse[i] = mean((test.pred - data_test$Y)^2)
}
test.mse
plot(1:20, test.mse, xlab="模型大小", ylab="最优模型测试均方误差", pch=1, type="o")

    QQ_1730198778092

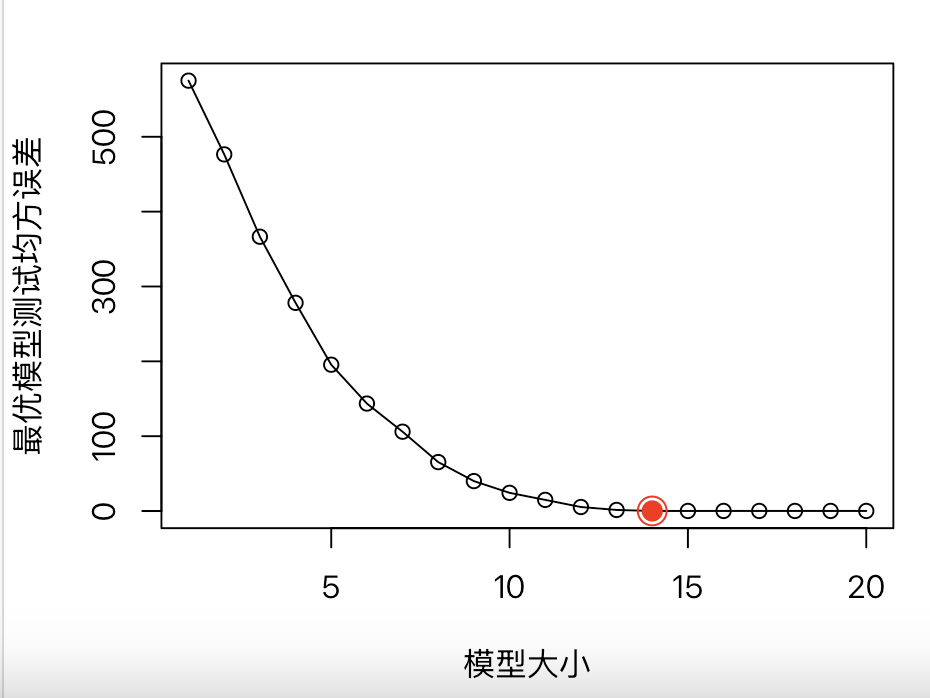
    QQ_1730199017180

  • (e)

    # 10.(e)
print(which.min(test.mse))
coef(lm.regsubsets(model,14))
## 可以发现在随着模型大小的提升，模型的预测变量数增加，灵活性增加
## 拟合情况更贴近真实情况，测试MSE降低直到最小值
## 但是随着模型大小进一步提升，预测变量数超过了真实情况
## 从而导致在训练集上出现过拟合情况，导致测试MSE增加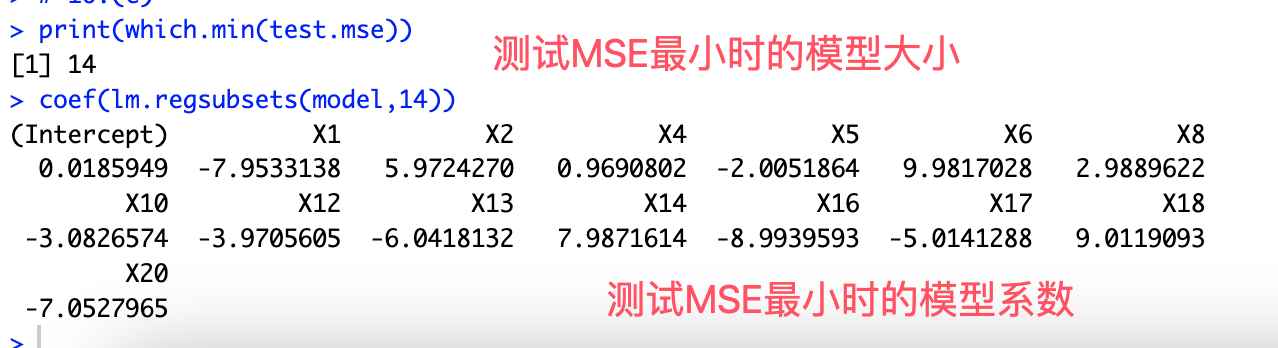

    QQ_1730199331740

  • (f)

    # 10.(f)
print(beta)
print(coef(lm.regsubsets(model,14)))
## 我们设置了5个β值为0，在这里我们得到最优模型大小为14（6个β被认为为0）
## 根据系数也可以看出，除了我们设置的五个β，这里认为β9也为0
## 通过对比模型系数和设定系数发现二者几乎相等

    QQ_1730208192126

  • (g)

    # 10.(g)
result = numeric(p)
for (i in 1:20) {
  model_coef_i = coef(lm.regsubsets(model, i)) # 获取大小为i的模型的系数
  coef_i = numeric(p) # 创建一个全零的系数向量
  coef_names = names(model_coef_i) # 提取变量名，排除截距项
  coef_names = coef_names[coef_names != "(Intercept)"] # 逻辑索引排除截距项
  coef_indices = match(coef_names, paste0("X", 1:p)) # 将变量名转换为索引并填入系数
  coef_i[coef_indices] = model_coef_i[coef_names]
  result[i] = sqrt(sum((beta - coef_i)^2))
}
par(mfrow = c(1, 2))
plot(1:20, test.mse, xlab="模型大小", ylab="最优模型测试均方误差", pch=1, type="o")
points(which.min(test.mse), min(test.mse), col="red", cex=2, pch=20)
plot(1:20, result, xlab="模型大小", ylab="式子结果", pch=1, type="o")
points(which.min(result), min(result), col="red", cex=2, pch=20)
## 可以发现随着模型大小增加，两者先下降，并在模型大小为14时得到最小值
## 两个图像都展示了模型大小与模型拟合效果的关系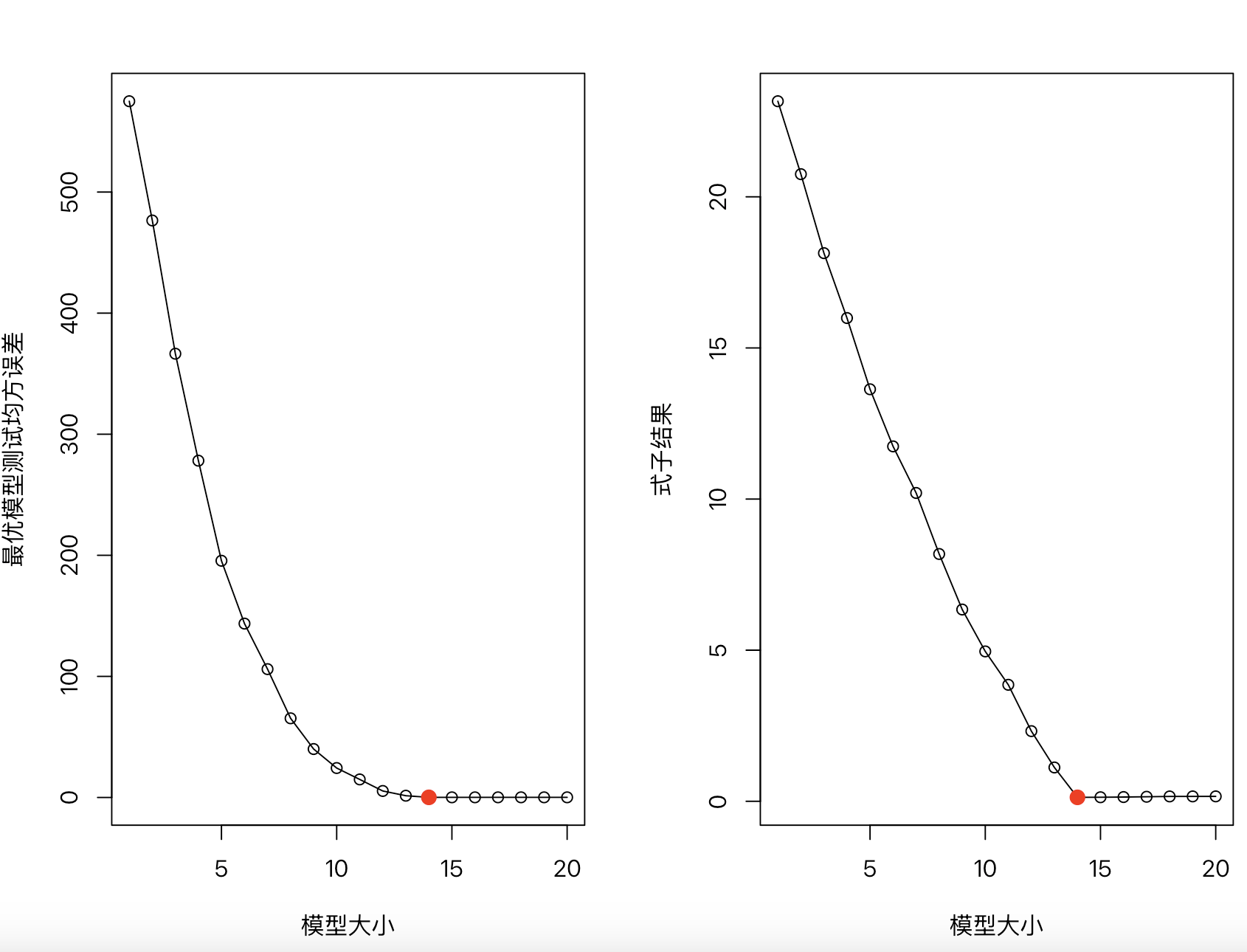

    QQ_1730211173616

  • 完整代码

    # 10.(a)
set.seed(1)
n = 1000 # 观测数
p = 20 # 特征数
X = matrix(rnorm(n*p), nrow = n, ncol = p)
eps = rnorm(n, mean=0, sd=0.3) # 生成标准差为0.3，均值为0的误差项
beta = sample(-10:10, 20) # 生成20个beta，取值在[-10,10]
beta[3] = 0
beta[7] = 0
beta[11] = 0
beta[15] = 0
beta[19] = 0
Y = X %*% beta + eps  # %*%为矩阵乘法运算符
data_XY = data.frame(X, Y) # 组合数据
​
# 10.(b)
set.seed(1)
train_indices = sample(1:n, size = 100)
data_train = data_XY[train_indices, ]
data_test = data_XY[-train_indices, ]
​
# 10.(c)
library(leaps)
set.seed(1)
model = regsubsets(Y~., data=data_train, nvmax=20) # 使用最优子集法，最大预测变量数20
model.summary = summary(model)
model.rss = model.summary$rss
model.mse = model.rss / n # 均方误差=RSS/样本数
print(model.mse)
plot(1:20, model.mse, xlab="模型大小", ylab="训练均方误差", pch=1, type="o")
​
# 10.(d)
library(HH)
test.mse = numeric(p) # 生成一个初始化为0、包含20元素的向量
for(i in 1:20){
  test.model = lm.regsubsets(model, i) # 从regsubsets对象中提取指定大小的模型
  test.pred = predict(test.model, data_test)
  test.mse[i] = mean((test.pred - data_test$Y)^2)
}
test.mse
plot(1:20, test.mse, xlab="模型大小", ylab="最优模型测试均方误差", pch=1, type="o")
points(which.min(test.mse), min(test.mse), col="red", cex=2, pch=20)
​
# 10.(e)
print(which.min(test.mse))
coef(lm.regsubsets(model,14))
## 可以发现在随着模型大小的提升，模型的预测变量数增加，灵活性增加
## 拟合情况更贴近真实情况，测试MSE降低直到最小值
## 但是随着模型大小进一步提升，预测变量数超过了真实情况
## 从而导致在训练集上出现过拟合情况，导致测试MSE增加
​
# 10.(f)
print(beta)
print(coef(lm.regsubsets(model,14)))
## 我们设置了5个β值为0，在这里我们得到最优模型大小为14（6个β被认为为0）
## 根据系数也可以看出，除了我们设置的五个β，这里认为β9也为0
## 通过对比模型系数和设定系数发现二者几乎相等
​
# 10.(g)
result = numeric(p)
for (i in 1:20) {
  model_coef_i = coef(lm.regsubsets(model, i)) # 获取大小为i的模型的系数
  coef_i = numeric(p) # 创建一个全零的系数向量
  coef_names = names(model_coef_i) # 提取变量名，排除截距项
  coef_names = coef_names[coef_names != "(Intercept)"] # 逻辑索引排除截距项
  coef_indices = match(coef_names, paste0("X", 1:p)) # 将变量名转换为索引并填入系数
  coef_i[coef_indices] = model_coef_i[coef_names]
  result[i] = sqrt(sum((beta - coef_i)^2))
}
par(mfrow = c(1, 2))
plot(1:20, test.mse, xlab="模型大小", ylab="最优模型测试均方误差", pch=1, type="o")
points(which.min(test.mse), min(test.mse), col="red", cex=2, pch=20)
plot(1:20, result, xlab="模型大小", ylab="式子结果", pch=1, type="o")
points(which.min(result), min(result), col="red", cex=2, pch=20)
## 可以发现随着模型大小增加，两者先下降，并在模型大小为14时得到最小值
## 两个图像都展示了模型大小与模型拟合效果的关系