[课程资料] 高级统计方法书后习题（九）
本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。
本章为10.7节习题答案。
声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。
如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。
一、概念题
10.7.1
(a)
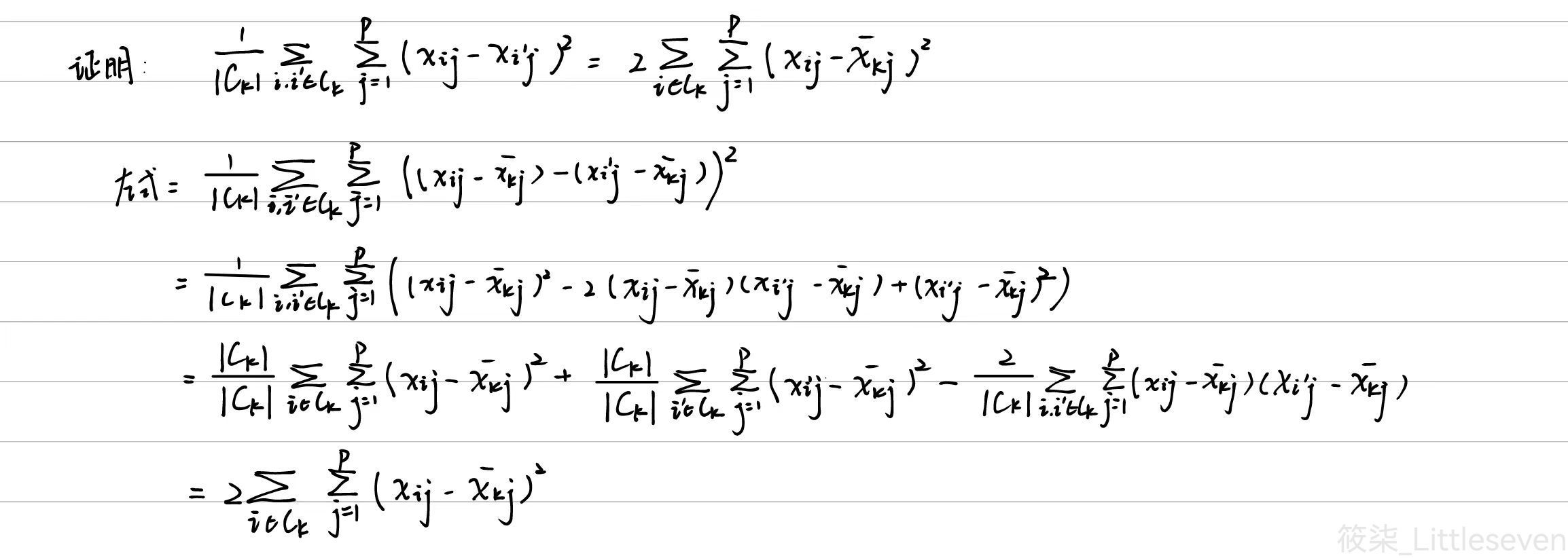
(b)
在K聚类算法的每次迭代中，算法通过一下两个步骤来减少目标函数的值：
重新分配样本。对于每个样本，计算它到每个簇中心之间的距离，并将其分配到距离最小的簇。
重新计算簇的中心。对于每个簇，计算新的均值作为簇的中心。
在上述等式中，左侧是计算簇内每一对样本之间的特征差异平方和，计算复杂度较高。右侧是计算每个样本到簇中心的差异平方和。在方程中表明了最小化每个聚类的欧氏距离平方和玉最小化每个聚类的簇内方差是等价的。
10.7.2
(a)
d = as.dist(matrix(c(0, 0.3, 0.4, 0.7, 0.3, 0, 0.5, 0.8, 0.4, 0.5, 0, 0.45, 0.7, 0.8, 0.45, 0), nrow=4)) plot(hclust(d, method="complete"))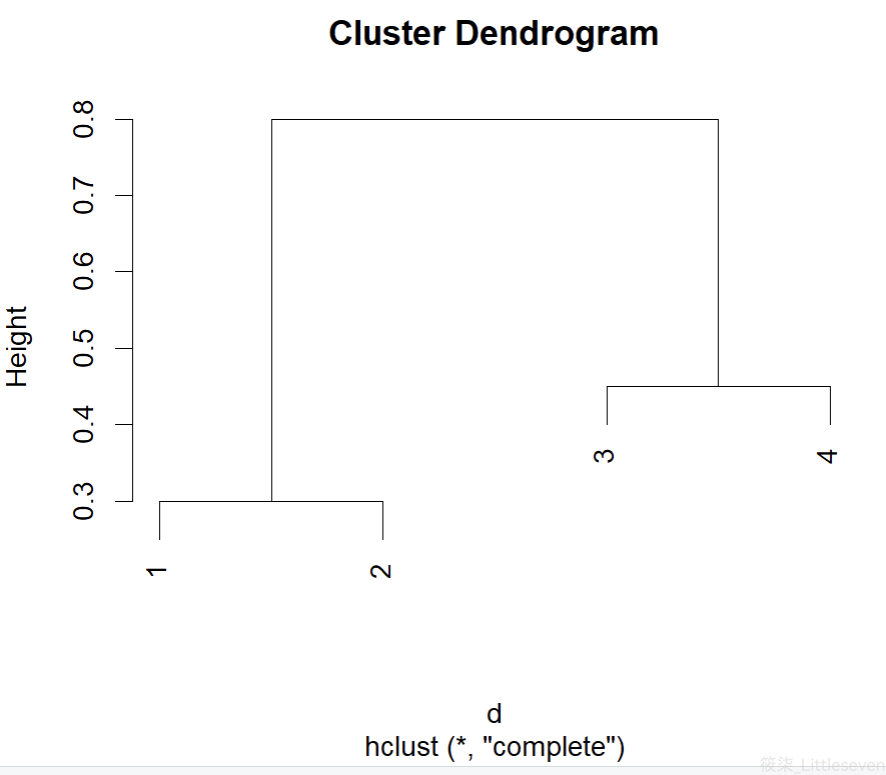
(b)
plot(hclust(d, method="single"))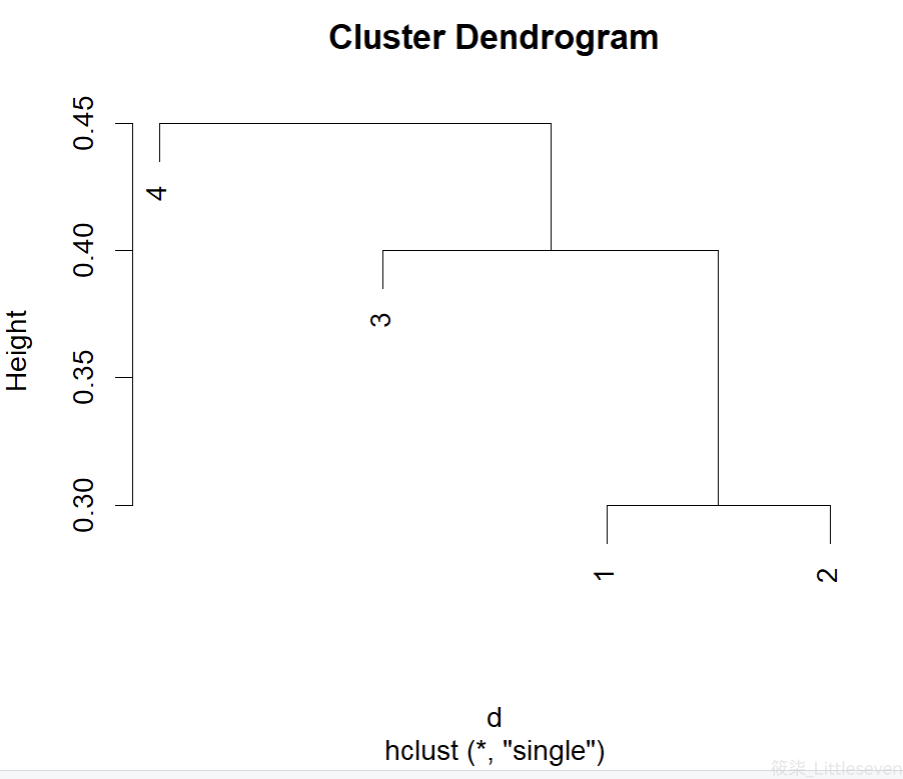
(c)
第一类：(1,2)
第二类：(3,4)
(d)
第一类：(1,2,3)
第二类：(4)
(e)
plot(hclust(d, method="complete"), labels=c(2,1,4,3))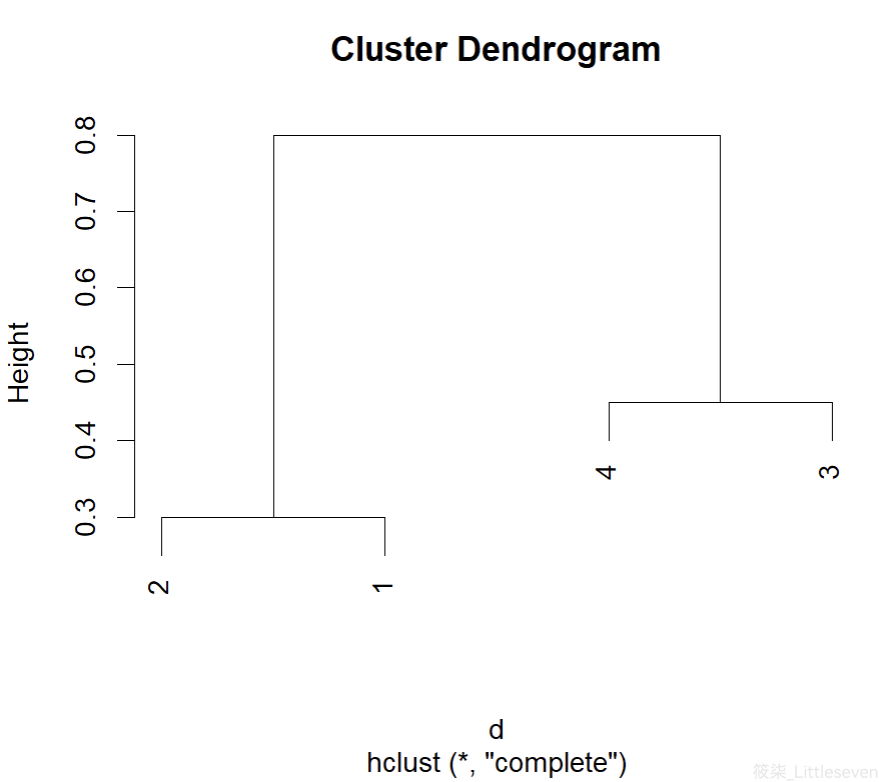
10.7.3
(a)
set.seed(1) x = cbind(c(1, 1, 0, 5, 6, 4), c(4, 3, 4, 1, 2, 0)) plot(x[,1], x[,2])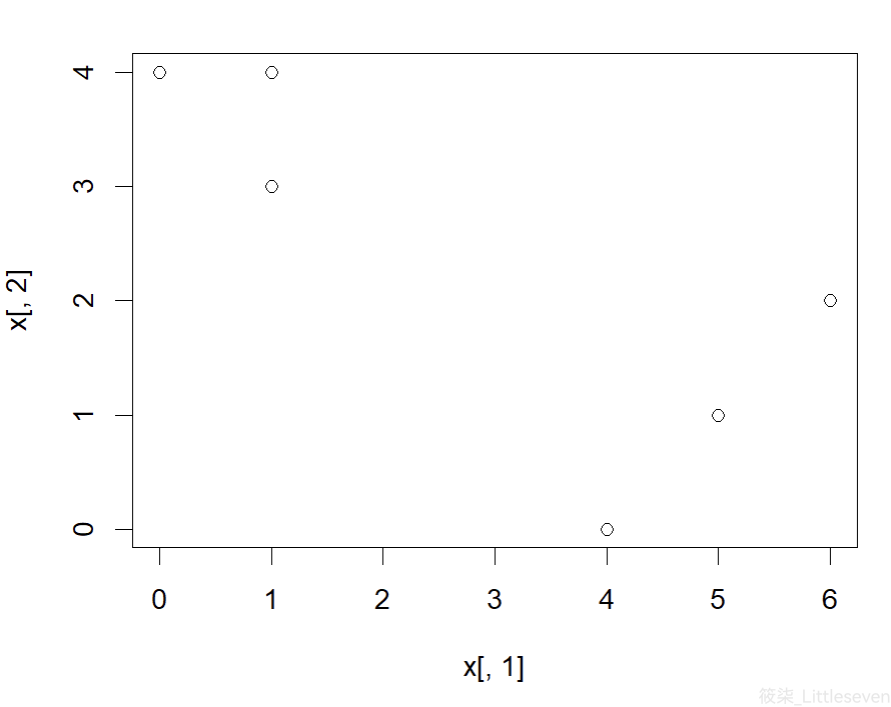
(b)
set.seed(1) labels = sample(2, nrow(x), replace=T) labels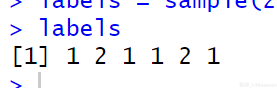
(c)
centroid1 = c(mean(x[labels==1, 1]), mean(x[labels==1, 2])) centroid2 = c(mean(x[labels==2, 1]), mean(x[labels==2, 2])) centroid1 centroid2 plot(x[,1], x[,2], col=(labels+1), pch=20, cex=2) points(centroid1[1], centroid1[2], col=2, pch=8) points(centroid2[1], centroid2[2], col=3, pch=8)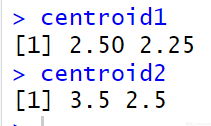
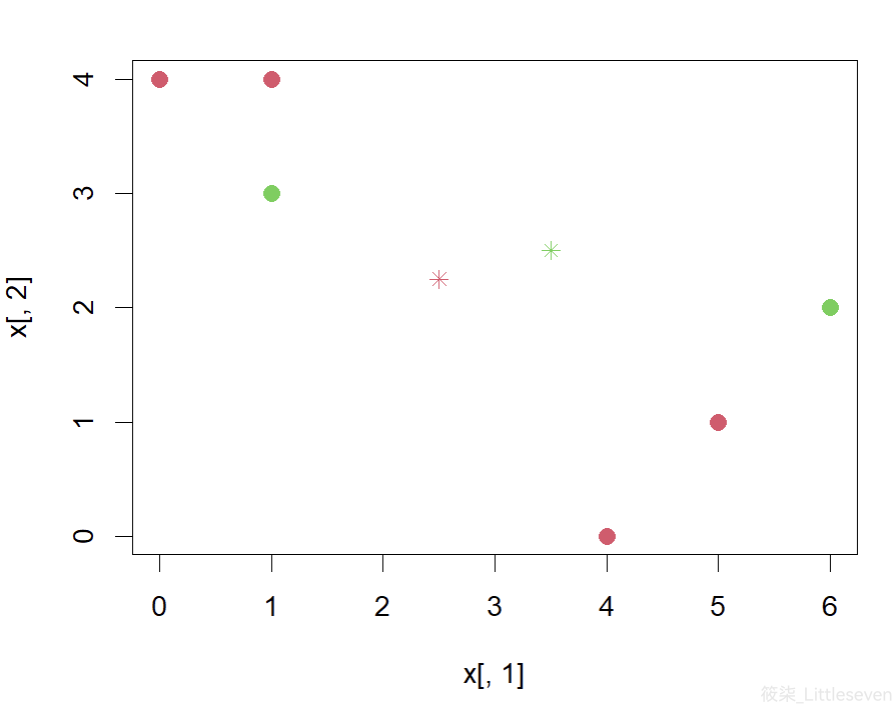
(d)
euclid = function(a, b) { return(sqrt((a[1] - b[1])^2 + (a[2]-b[2])^2)) } assign_labels = function(x, centroid1, centroid2) { labels = rep(NA, nrow(x)) for (i in 1:nrow(x)) { if (euclid(x[i,], centroid1) < euclid(x[i,], centroid2)) { labels[i] = 1 } else { labels[i] = 2 } } return(labels) } labels = assign_labels(x, centroid1, centroid2) labels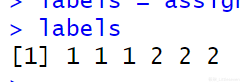
(e)
last_labels = rep(-1, 6) while (!all(last_labels == labels)) { last_labels = labels centroid1 = c(mean(x[labels==1, 1]), mean(x[labels==1, 2])) centroid2 = c(mean(x[labels==2, 1]), mean(x[labels==2, 2])) print(centroid1) print(centroid2) labels = assign_labels(x, centroid1, centroid2) } labels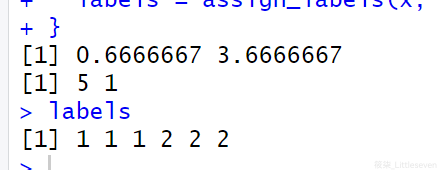
(f)
plot(x[,1], x[,2], col=(labels+1), pch=20, cex=2) points(centroid1[1], centroid1[2], col=2, pch=8) points(centroid2[1], centroid2[2], col=3, pch=8)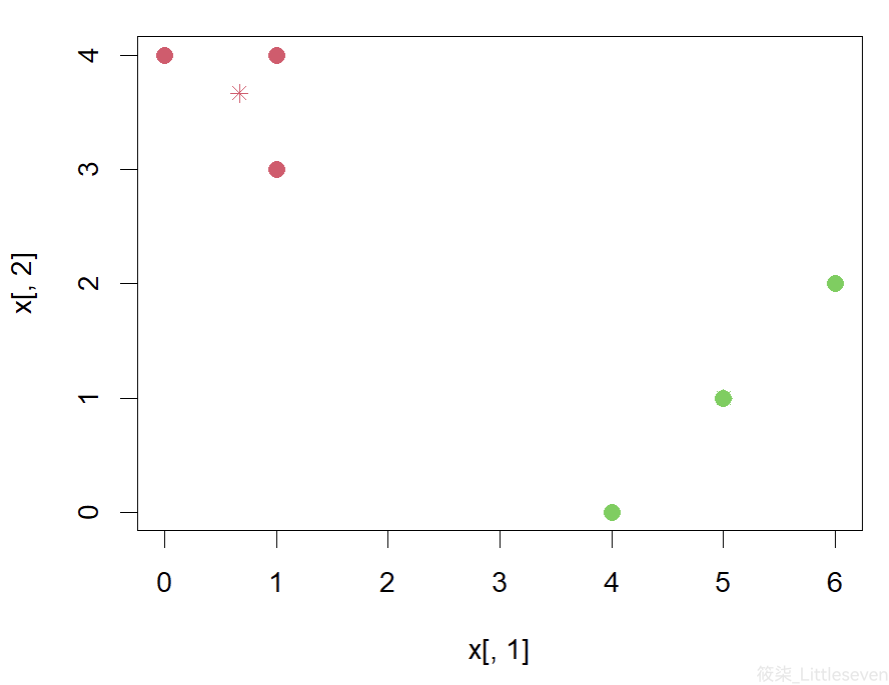
10.7.4
(a)
对于 {1,2,3} 和 {4,5} 两个类在最短距离法和最长距离法中都汇聚的情况：
最短距离法：由于 {1,2,3} 和 {4,5} 之间可能存在较小的最短距离（例如，1和4之间的距离），这可能导致这两个类在最短距离法中较早地汇聚。
最长距离法：在最长距离法中，需要考虑类中所有点之间的最大距离。如果 {1,2,3} 和 {4,5} 之间的最大距离较大，那么这两个类可能不会在早期汇聚。
因此，如果这两个类在两种方法中都汇聚，最短距离法中的汇聚位置可能更高（即更早汇聚），而最长距离法中的汇聚位置可能更低（即更晚汇聚）。
(b)
对于 {5} 和 {6} 两个类在最短距离法和最长距离法中都汇聚的情况：
最短距离法：由于 {5} 和 {6} 之间可能存在较小的最短距离，这可能导致这两个类在最短距离法中较早地汇聚。
最长距离法：同样，如果 {5} 和 {6} 之间的最大距离较小，这两个类也可能在最长距离法中较早地汇聚。
在这种情况下，如果这两个类在两种方法中都汇聚，它们的汇聚高度可能相同，因为它们之间的距离较小，无论是最短距离还是最长距离，都可能导致它们在相似的位置汇聚。
二、应用题
10.7.10
(a)
# 10.(a) set.seed(42) # 设置随机种子以确保结果可重复 n_obs = 20 # 每个类的观测数 n_vars = 50 # 每个观测的变量数 n_classes = 3 # 类的数量 # 创建每个类的数据 class1 = matrix(rnorm(n_obs * n_vars, mean=0, sd=1), nrow=n_obs, ncol=n_vars) class2 = matrix(rnorm(n_obs * n_vars, mean=5, sd=1), nrow=n_obs, ncol=n_vars) class3 = matrix(rnorm(n_obs * n_vars, mean=10, sd=1), nrow=n_obs, ncol=n_vars) # 合并数据集 data = rbind(class1, class2, class3) labels = factor(rep(1:n_classes, each=n_obs)) # 真实的类标签(b)
# 10.(b) # 进行PCA分析 pca_result = prcomp(data, scale. = TRUE) # 绘制前两个主成分得分的散点图 plot(pca_result$x[, 1:2], col=labels, pch=19, xlab="PC1", ylab="PC2", main="PCA: First Two Principal Components") legend("topright", legend=levels(labels), col=1:n_classes, pch=19)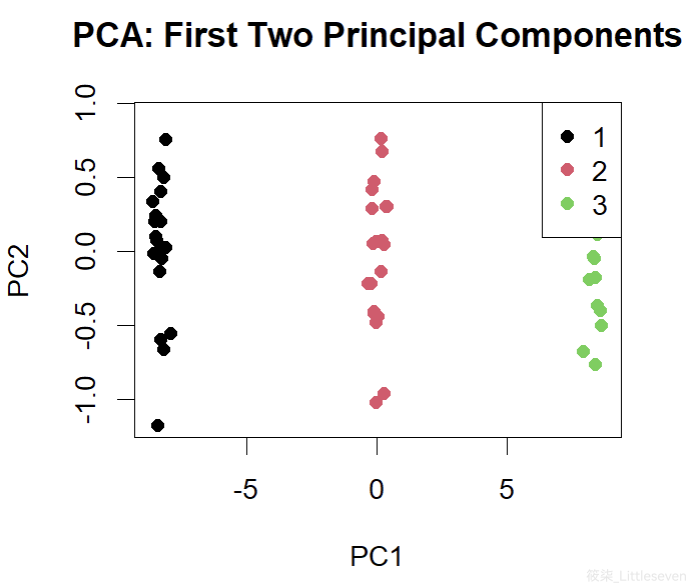
(c)
# 10.(c) # 进行K=3的K均值聚类 set.seed(42) # 设置随机种子以确保结果可重复 kmeans_result_3 = kmeans(data, centers=3) # 比较K均值聚类结果和真实类标签 table(labels, kmeans_result_3$cluster)
(a-2)
# 10.(a-2) # 进行K=2的K均值聚类 set.seed(42) kmeans_result_2 = kmeans(data, centers=2) # 比较结果 table(labels, kmeans_result_2$cluster)
(b-2)
# 10.(b-2) # 进行K=4的K均值聚类 set.seed(42) kmeans_result_4 = kmeans(data, centers=4) # 比较结果 table(labels, kmeans_result_4$cluster)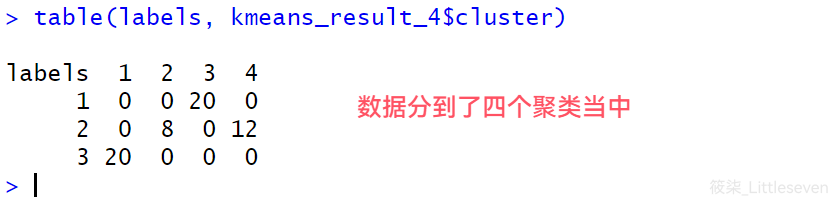
(c-2)
# 10.(c-2) # 使用前两个主成分进行K=3的K均值聚类 set.seed(42) pca_kmeans_result_3 = kmeans(pca_result$x[, 1:2], centers=3) # 比较结果 table(labels, pca_kmeans_result_3$cluster)
(d)
# 10.(d) # 对数据进行标准化 scaled_data = scale(data) # 进行K=3的K均值聚类 set.seed(42) scaled_kmeans_result_3 = kmeans(scaled_data, centers=3) # 比较结果 table(labels, scaled_kmeans_result_3$cluster)
完整代码
# 10.(a) set.seed(42) # 设置随机种子以确保结果可重复 n_obs = 20 # 每个类的观测数 n_vars = 50 # 每个观测的变量数 n_classes = 3 # 类的数量 # 创建每个类的数据 class1 = matrix(rnorm(n_obs * n_vars, mean=0, sd=1), nrow=n_obs, ncol=n_vars) class2 = matrix(rnorm(n_obs * n_vars, mean=5, sd=1), nrow=n_obs, ncol=n_vars) class3 = matrix(rnorm(n_obs * n_vars, mean=10, sd=1), nrow=n_obs, ncol=n_vars) # 合并数据集 data = rbind(class1, class2, class3) labels = factor(rep(1:n_classes, each=n_obs)) # 真实的类标签 # 10.(b) # 进行PCA分析 pca_result = prcomp(data, scale. = TRUE) # 绘制前两个主成分得分的散点图 plot(pca_result$x[, 1:2], col=labels, pch=19, xlab="PC1", ylab="PC2", main="PCA: First Two Principal Components") legend("topright", legend=levels(labels), col=1:n_classes, pch=19) # 10.(c) # 进行K=3的K均值聚类 set.seed(42) # 设置随机种子以确保结果可重复 kmeans_result_3 = kmeans(data, centers=3) # 比较K均值聚类结果和真实类标签 table(labels, kmeans_result_3$cluster) # 10.(a-2) # 进行K=2的K均值聚类 set.seed(42) kmeans_result_2 = kmeans(data, centers=2) # 比较结果 table(labels, kmeans_result_2$cluster) # 10.(b-2) # 进行K=4的K均值聚类 set.seed(42) kmeans_result_4 = kmeans(data, centers=4) # 比较结果 table(labels, kmeans_result_4$cluster) # 10.(c-2) # 使用前两个主成分进行K=3的K均值聚类 set.seed(42) pca_kmeans_result_3 = kmeans(pca_result$x[, 1:2], centers=3) # 比较结果 table(labels, pca_kmeans_result_3$cluster) # 10.(d) # 对数据进行标准化 scaled_data = scale(data) # 进行K=3的K均值聚类 set.seed(42) scaled_kmeans_result_3 = kmeans(scaled_data, centers=3) # 比较结果 table(labels, scaled_kmeans_result_3$cluster)
本文是原创文章，采用 CC BY-NC-SA 4.0 协议，完整转载请注明来自 筱柒_Littleseven
阅读建议
评论
匿名评论
隐私政策
你无需删除空行，直接评论以获取最佳展示效果