[课程资料] 高级统计方法书后习题（七）

本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为7.9节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

7.9.1

7.9.2

7.9.3

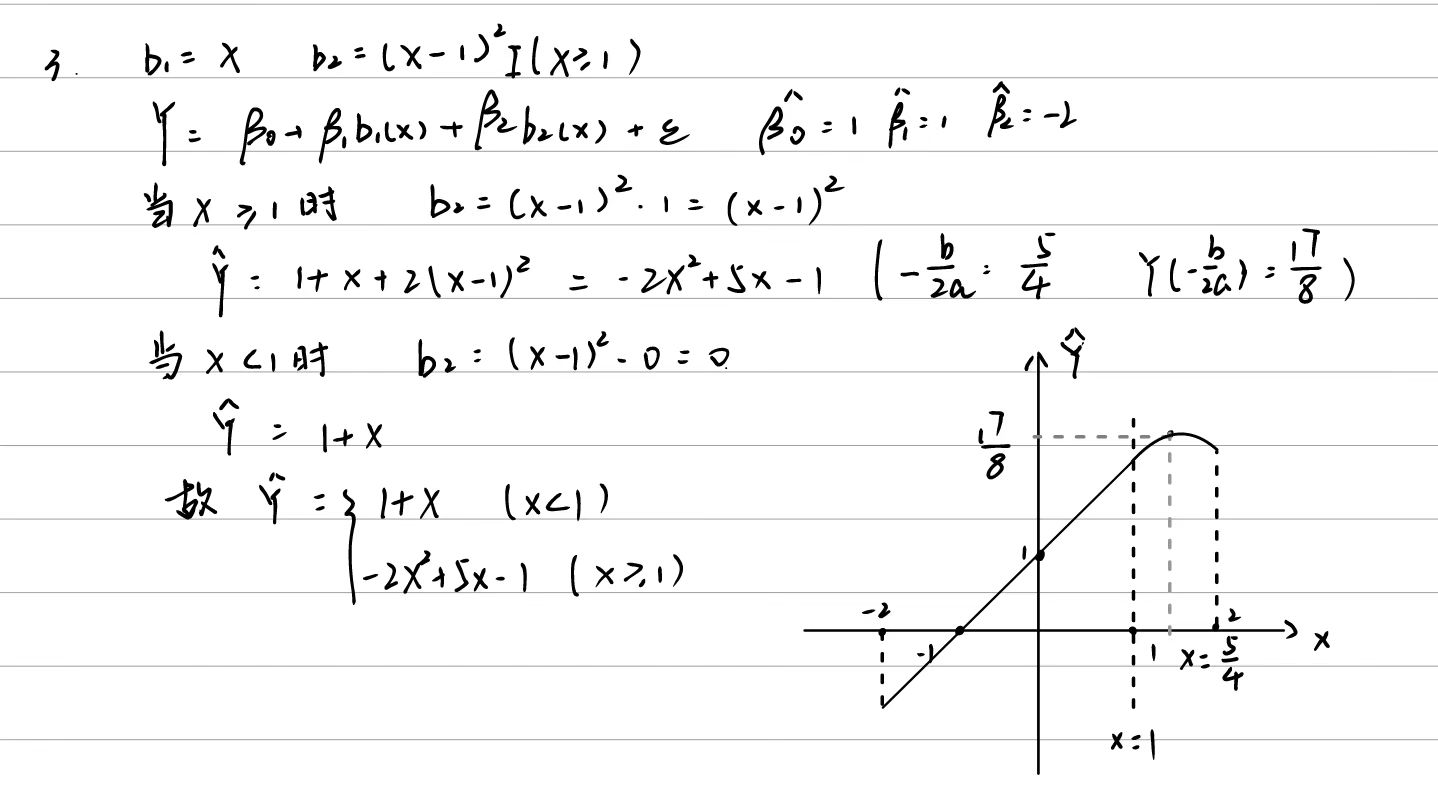
7.9.4

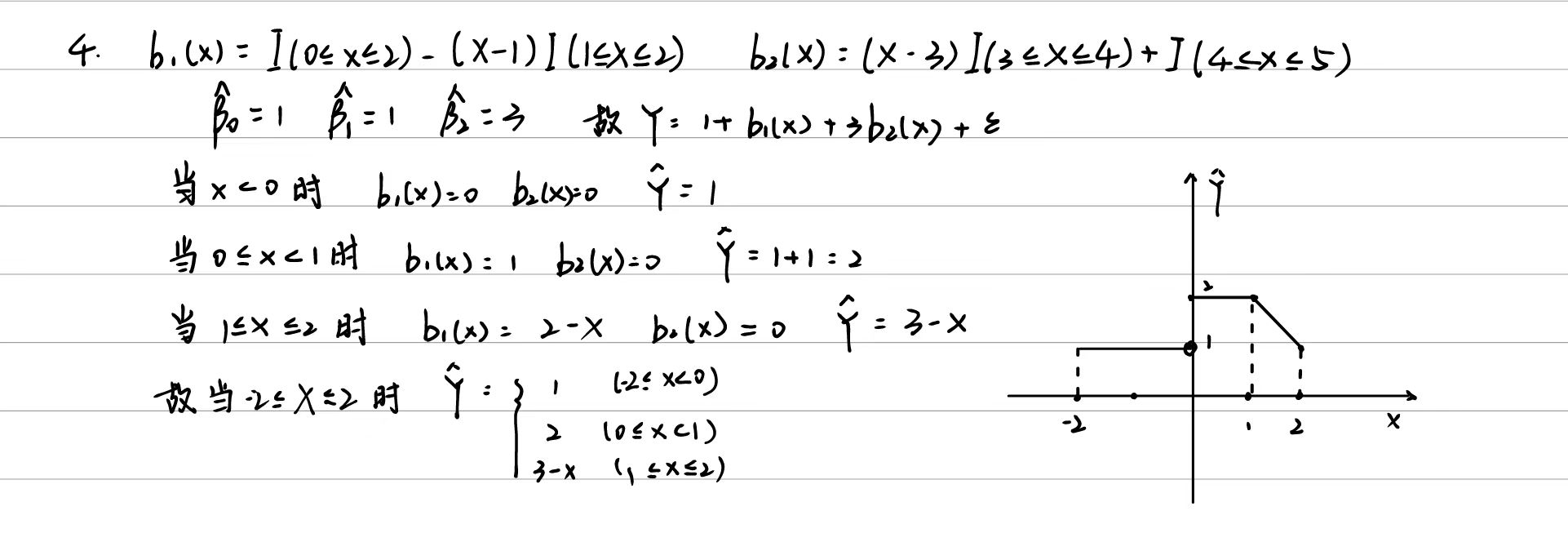
7.9.5

二、应用题

7.9.9

• (a)

  # 9.(a)
  library(MASS)
  model = lm(nox~poly(dis, 3), data = Boston)
  summary(model)
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox")
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) ## 设置平滑的dis序列
  nox_pred = predict(model, newdata = data.frame(dis=dis_seq)) ## 进行预测
  lines(dis_seq, nox_pred, col="red") ## 绘制三次回归预测图像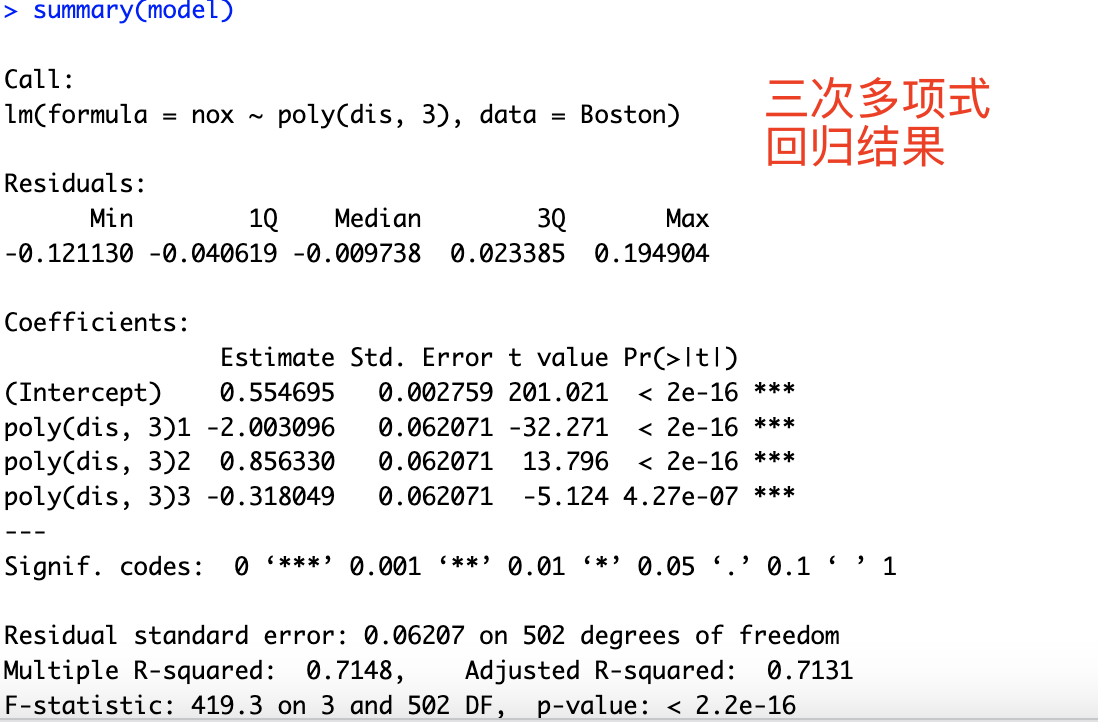
  

  

  

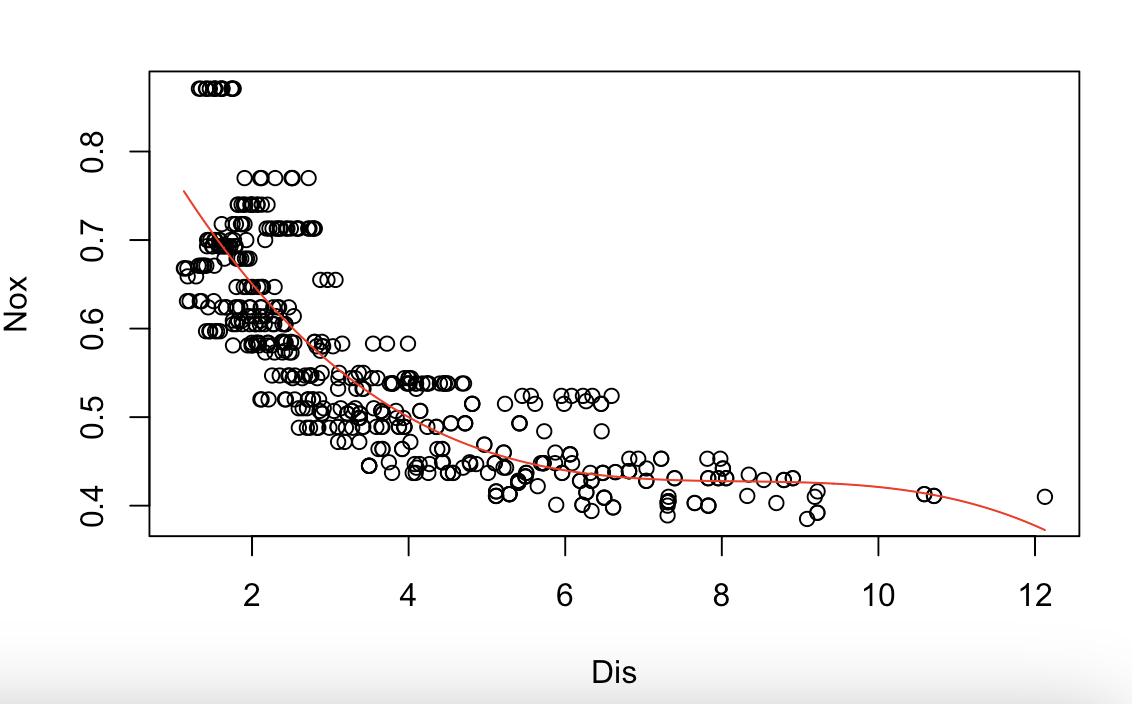
• (b)

  # 9.(b)
  rss = numeric(10) # 10个参数的向量（数组）
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox", col="grey")
  colors = rainbow(10) # 10种颜色
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) 
  for(i in 1:10) {
    model = lm(nox ~ poly(dis, i), data = Boston)
    nox_pred = predict(model, newdata = data.frame(dis=dis_seq))
    lines(dis_seq, nox_pred, col=colors[i], lwd=2)
    rss[i] = sum(residuals(model)^2)
  }
  legend("topright", legend = 1:10, col=colors, lwd=2, cex=0.5)
  plot(1:10, rss, xlab="Degree", ylab="RSS", type="b")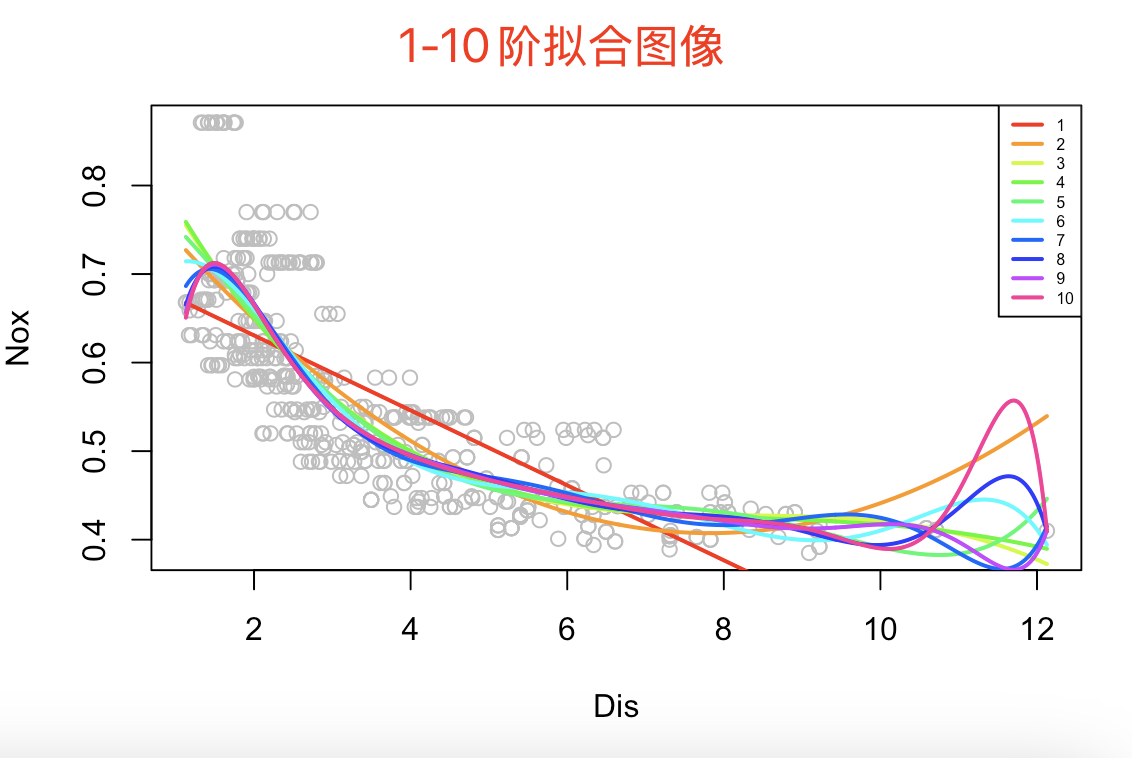
  

  

  

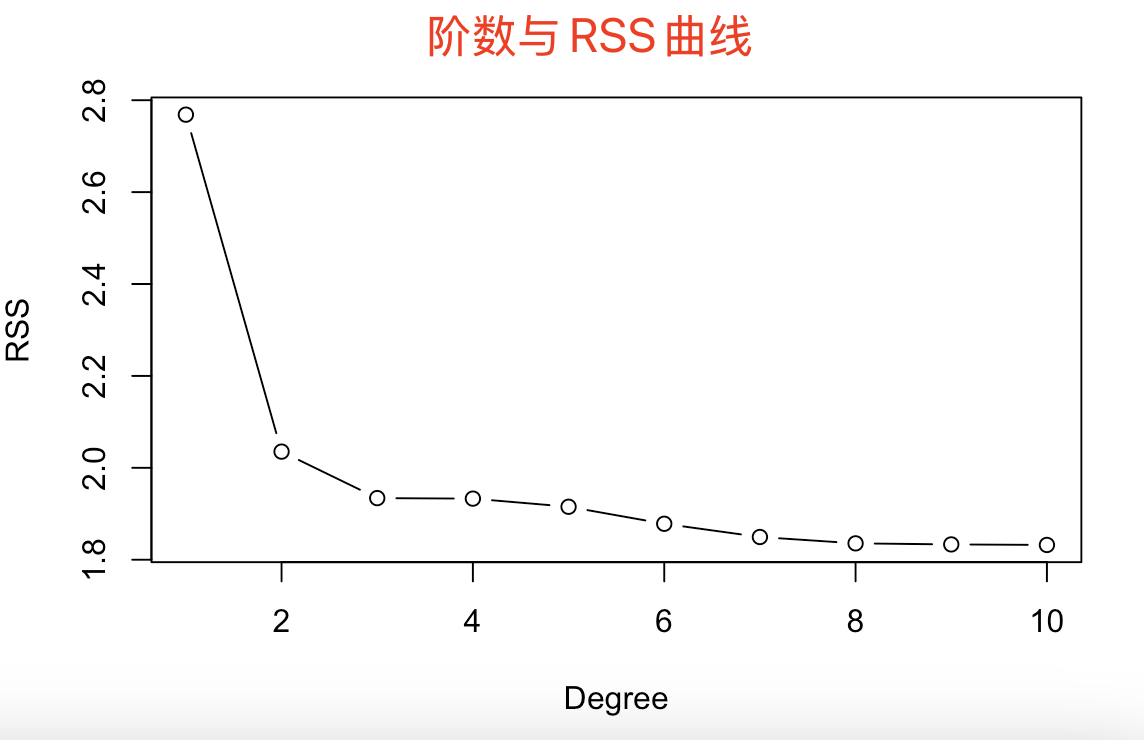
• (c)

  # 9.(c)
  library(boot)
  set.seed(1)
  cv.mse = numeric(10)
  for(i in 1:10) {
    glm.fit = glm(nox~poly(dis, i), data=Boston)
    cv.mse[i] = cv.glm(Boston, glm.fit, K=10)$delta[1]
  }
  plot(1:10, cv.mse, xlab="Degree", ylab="cv-MSE", type="b")
  points(which.min(cv.mse), min(cv.mse), pch=1, col="red") ## 找到使MSE最小的阶数
  ## 在图中可以看出当阶数为4的时候交叉验证均方误差最小，所以4阶模型最优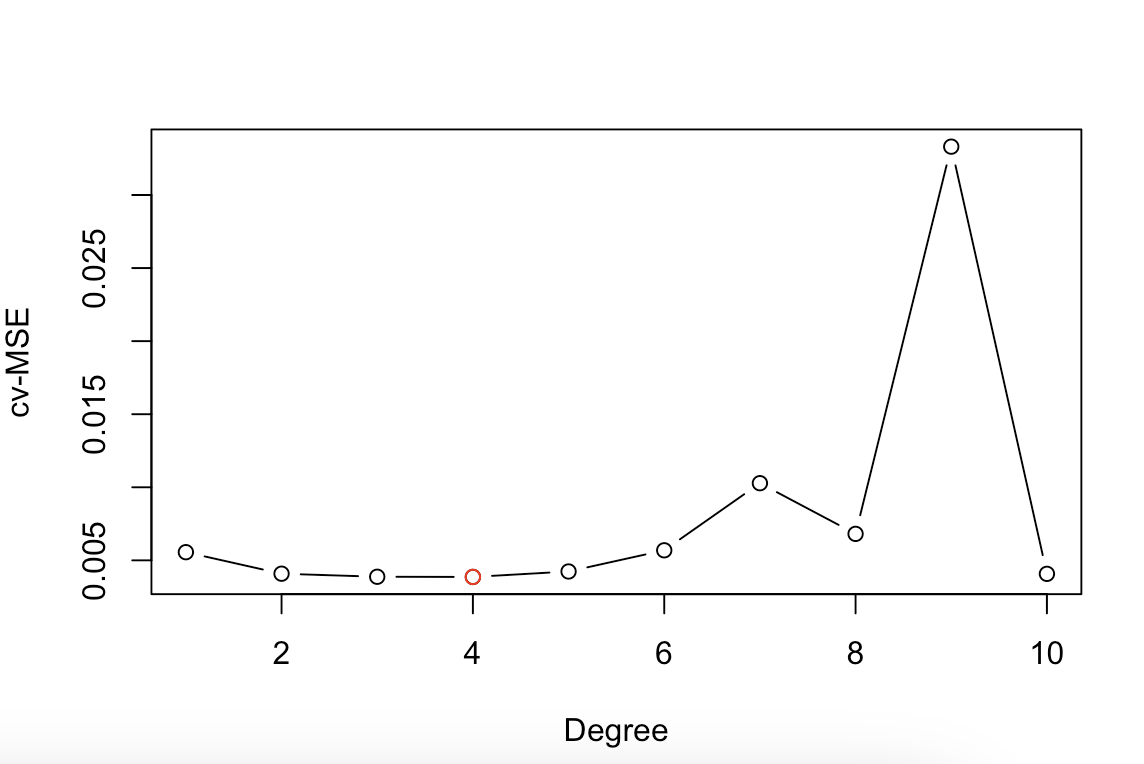
  

  

• (d)

  # 9.(d)
  library(splines) 
  ## 当前自由度(df)要求为4，如果选择3阶（三次样条），那么结点数量为4-3=1个
  ## 这里我们选择结点放在中位数位置
  knots = quantile(Boston$dis, probs=0.5)
  knots
  model = lm(nox ~ bs(dis, df=4, knots=knots), data = Boston)
  summary(model)
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) 
  nox_pred = predict(model, newdata = data.frame(dis=dis_seq))
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox", col="grey")
  lines(dis_seq, nox_pred, col="red", lwd=2)
  

  

  

  

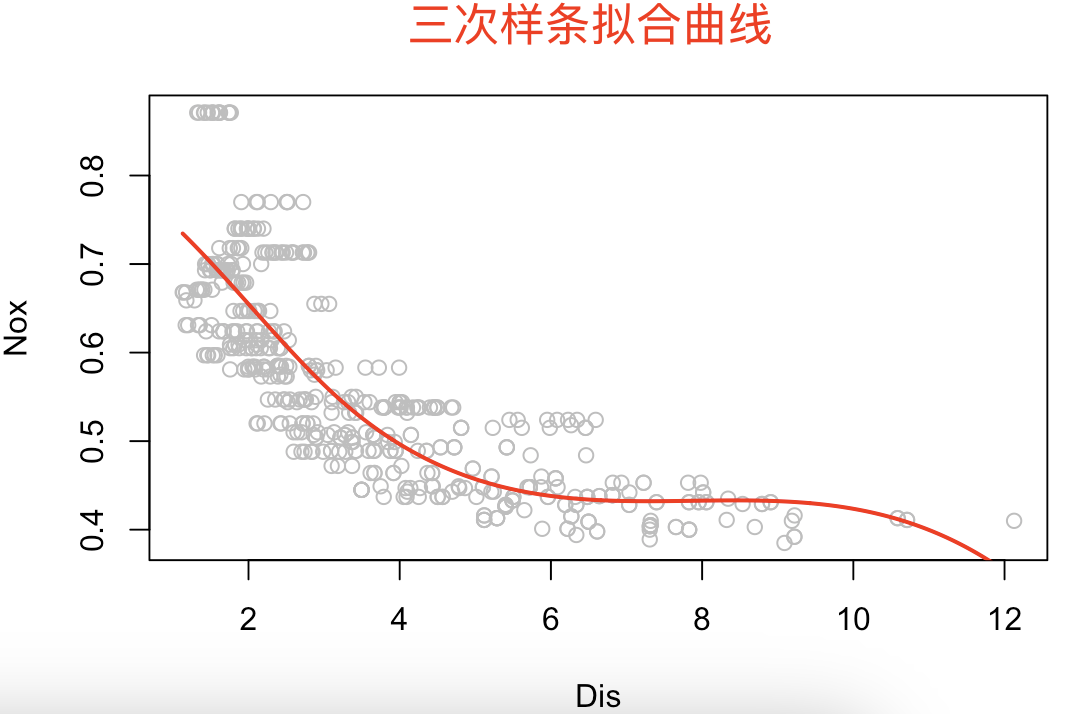
• (e)

  # 9.(e) # 选择df=4~10的区间
  rss = numeric(10) 
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox", col="grey")
  colors = rainbow(7) # 10种颜色
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) 
  for(i in 4:10) {
    model = lm(nox ~ bs(dis, df=i), data = Boston)
    nox_pred = predict(model, newdata = data.frame(dis=dis_seq))
    lines(dis_seq, nox_pred, col=colors[i-3], lwd=2)
    rss[i] = sum(residuals(model)^2)
  }
  legend("topright", legend = 4:10, col=colors, lwd=2, cex=0.5)
  plot(4:10, rss[4:10], xlab="Degree", ylab="RSS", type="b")
  ## 随着df增加，模型拟合效果更好，RSS更低（但是可能出现过拟合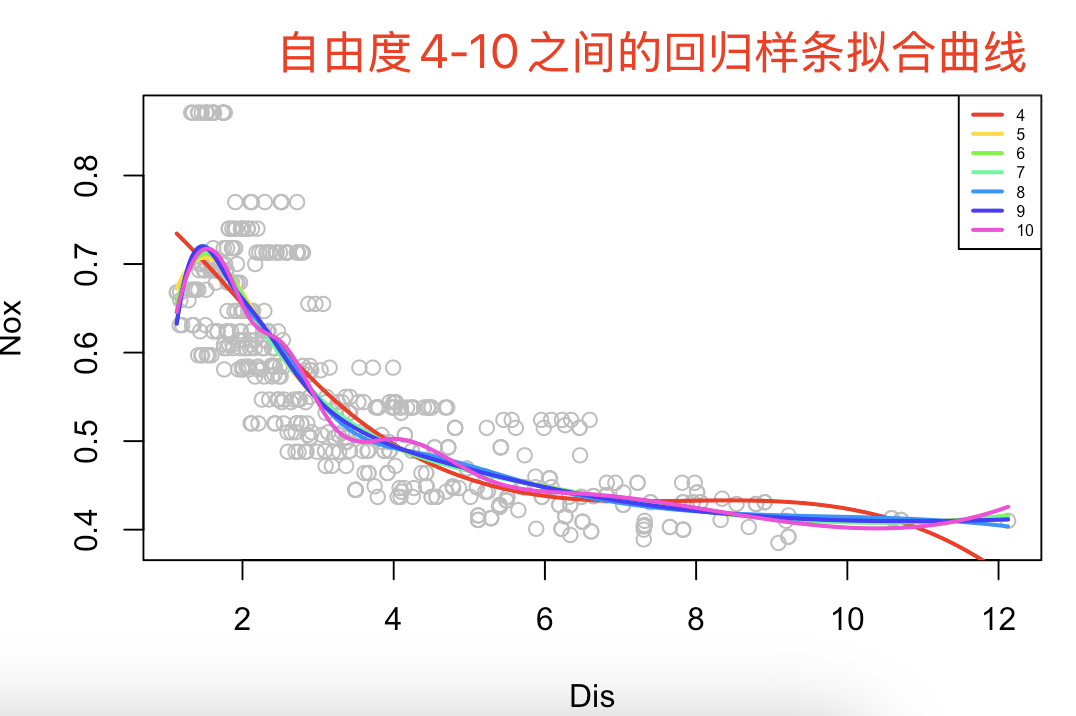
  

  

  

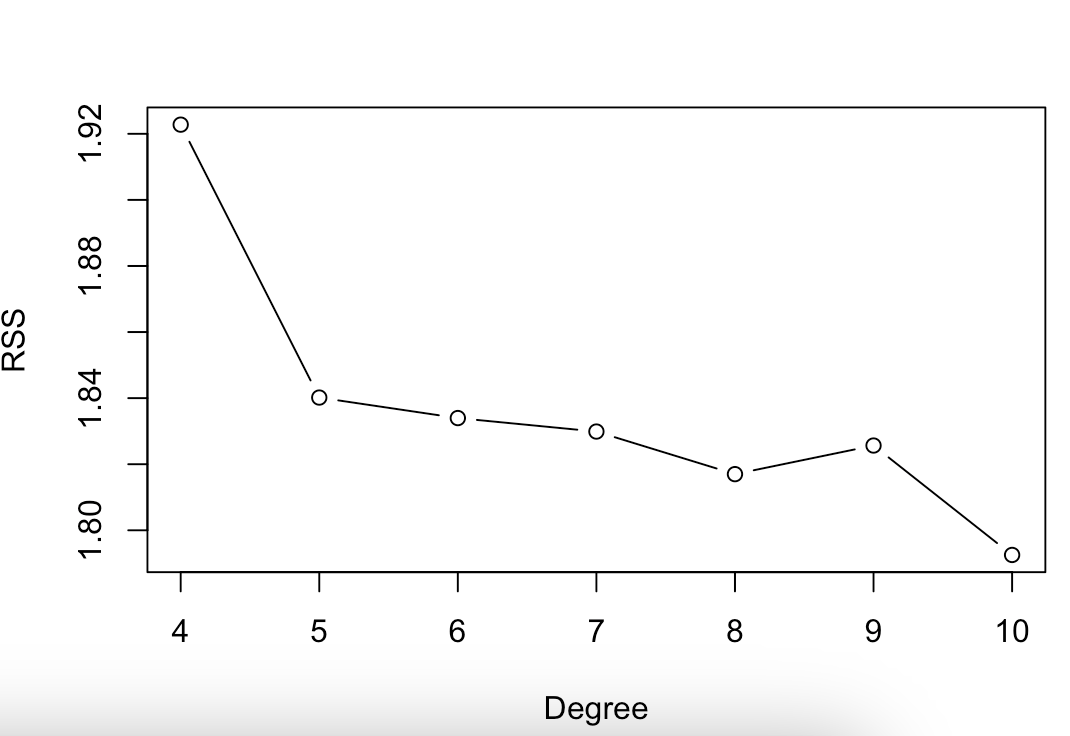
• (f)

  # 9.(f)
  set.seed(1)
  cv.mse = numeric(15)
  for(i in 1:15) {
    glm.fit = glm(nox~bs(dis, df=i), data=Boston)
    cv.mse[i] = cv.glm(Boston, glm.fit, K=10)$delta[1]
  }
  plot(1:15, cv.mse, xlab="Degree", ylab="cv-MSE", type="b")
  points(which.min(cv.mse), min(cv.mse), pch=1, col="red") 
  ## 由图中可以得出阶数为10的时候交叉验证均方误差最小，拟合效果最好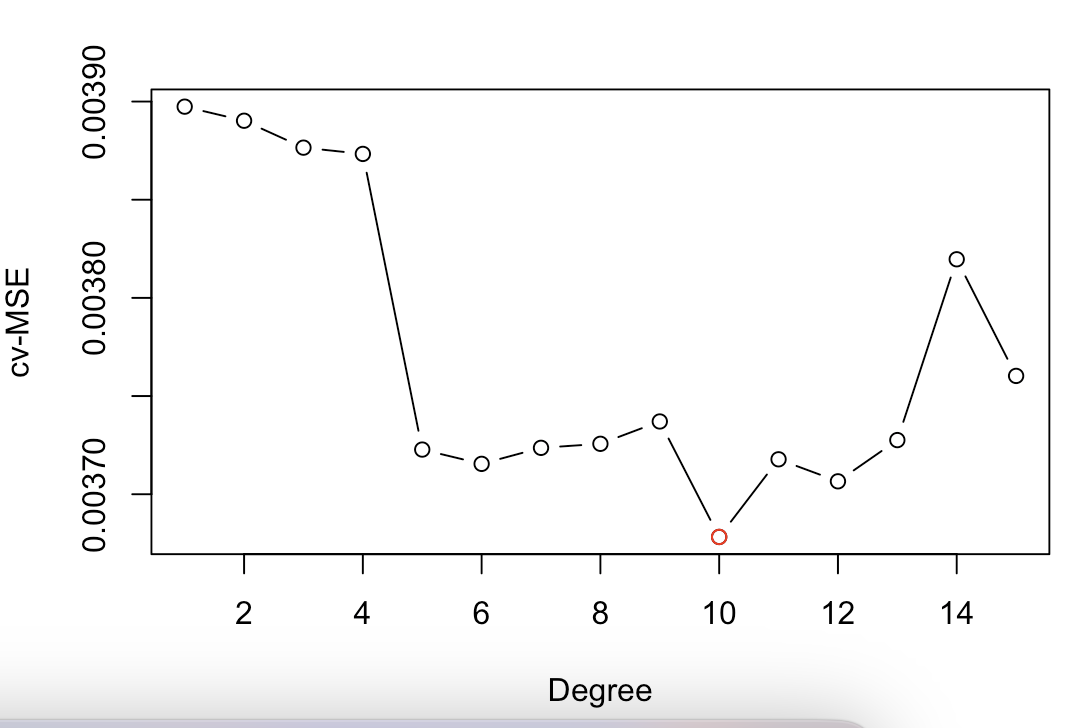
  

  

• 完整代码

  # 9.(a)
  library(MASS)
  model = lm(nox~poly(dis, 3), data = Boston)
  summary(model)
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox")
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) ## 设置平滑的dis序列
  nox_pred = predict(model, newdata = data.frame(dis=dis_seq)) ## 进行预测
  lines(dis_seq, nox_pred, col="red") ## 绘制三次回归预测图像
  
  # 9.(b)
  rss = numeric(10) # 10个参数的向量（数组）
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox", col="grey")
  colors = rainbow(10) # 10种颜色
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) 
  for(i in 1:10) {
    model = lm(nox ~ poly(dis, i), data = Boston)
    nox_pred = predict(model, newdata = data.frame(dis=dis_seq))
    lines(dis_seq, nox_pred, col=colors[i], lwd=2)
    rss[i] = sum(residuals(model)^2)
  }
  legend("topright", legend = 1:10, col=colors, lwd=2, cex=0.5)
  plot(1:10, rss, xlab="Degree", ylab="RSS", type="b")
  
  # 9.(c)
  library(boot)
  set.seed(1)
  cv.mse = numeric(10)
  for(i in 1:10) {
    glm.fit = glm(nox~poly(dis, i), data=Boston)
    cv.mse[i] = cv.glm(Boston, glm.fit, K=10)$delta[1]
  }
  plot(1:10, cv.mse, xlab="Degree", ylab="cv-MSE", type="b")
  points(which.min(cv.mse), min(cv.mse), pch=1, col="red") ## 找到使MSE最小的阶数
  ## 在图中可以看出当阶数为4的时候交叉验证均方误差最小，所以4阶模型最优
  
  # 9.(d)
  library(splines) 
  ## 当前自由度(df)要求为4，如果选择3阶（三次样条），那么结点数量为4-3=1个
  ## 这里我们选择结点放在中位数位置
  knots = quantile(Boston$dis, probs=0.5)
  knots
  model = lm(nox ~ bs(dis, df=4, knots=knots), data = Boston)
  summary(model)
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) 
  nox_pred = predict(model, newdata = data.frame(dis=dis_seq))
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox", col="grey")
  lines(dis_seq, nox_pred, col="red", lwd=2)
  
  # 9.(e) # 选择df=4~10的区间
  rss = numeric(10) 
  plot(Boston$dis, Boston$nox, xlab="Dis", ylab="Nox", col="grey")
  colors = rainbow(7) # 10种颜色
  dis_seq = seq(min(Boston$dis), max(Boston$dis), length.out=length(Boston$dis)) 
  for(i in 4:10) {
    model = lm(nox ~ bs(dis, df=i), data = Boston)
    nox_pred = predict(model, newdata = data.frame(dis=dis_seq))
    lines(dis_seq, nox_pred, col=colors[i-3], lwd=2)
    rss[i] = sum(residuals(model)^2)
  }
  legend("topright", legend = 4:10, col=colors, lwd=2, cex=0.5)
  plot(4:10, rss[4:10], xlab="Degree", ylab="RSS", type="b")
  ## 随着df增加，模型拟合效果更好，RSS更低（但是可能出现过拟合）
  
  # 9.(f)
  set.seed(1)
  cv.mse = numeric(15)
  for(i in 1:15) {
    glm.fit = glm(nox~bs(dis, df=i), data=Boston)
    cv.mse[i] = cv.glm(Boston, glm.fit, K=10)$delta[1]
  }
  plot(1:15, cv.mse, xlab="Degree", ylab="cv-MSE", type="b")
  points(which.min(cv.mse), min(cv.mse), pch=1, col="red") 
  ## 由图中可以得出阶数为10的时候交叉验证均方误差最小，拟合效果最好
  

7.9.10

• (a)

  # 10.(a)
  library(ISLR)
  set.seed(1) 
  n = nrow(College) ## 数据总数
  p = ncol(College) - 1 ## 最大维度
  train = sample(1:n, size=round(0.7*n))
  College.train = College[train, ]
  College.test = College[-train, ]
  library(leaps)
  model_forward = regsubsets(Outstate~., data=College.train, nvmax=p, method="forward")
  model_forward_summary = summary(model_forward)
  par(mfrow=c(2,2))
  plot(1:p, model_forward_summary$cp, xlab="Degree", ylab="Cp", type="o")
  points(which.min(model_forward_summary$cp), min(model_forward_summary$cp), col="red", pch=16)
  plot(1:p, model_forward_summary$bic, xlab="Degree", ylab="BIC", type="o")
  points(which.min(model_forward_summary$bic), min(model_forward_summary$bic), col="red", pch=16)
  plot(1:p, model_forward_summary$adjr2, xlab="Degree", ylab="AdjR2", type="o")
  points(which.max(model_forward_summary$adjr2), max(model_forward_summary$adjr2), col="red", pch=16)
  ## 根据图像可以得出模型大小为13的时候效果最好
  coef(model_forward, 13)
  ## 可以看出包含如列表的13个变量，系数如下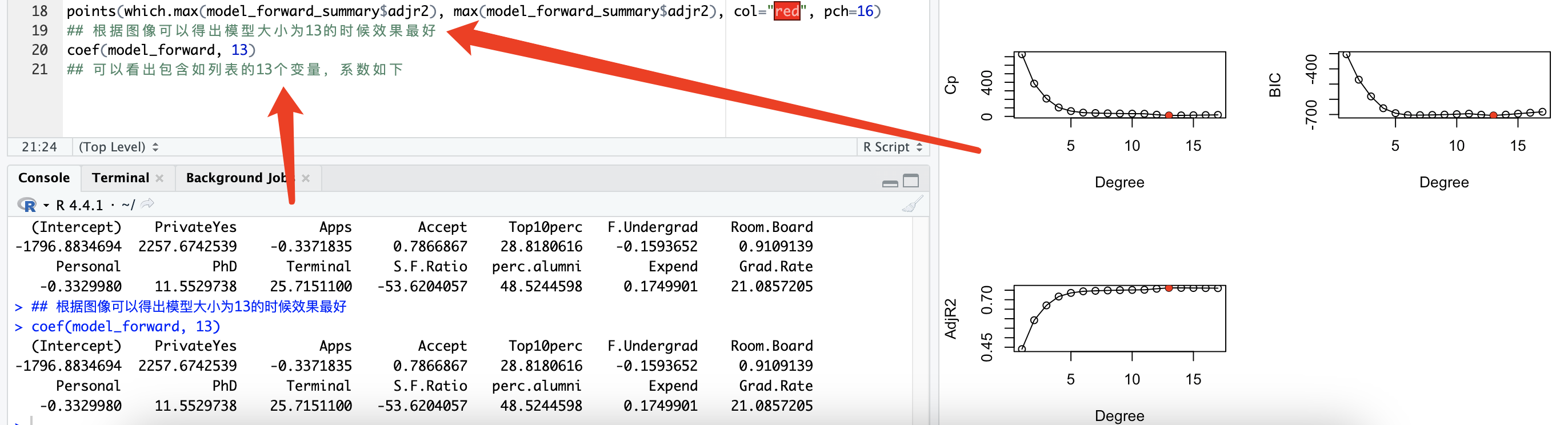
  

  

• (b)

  # 10.(b)
  library(gam)
  model_gam = gam(Outstate ~ Private + s(Apps) + s(Accept) + s(Top10perc) + s(F.Undergrad) + 
                    s(Room.Board) + s(Personal) + s(PhD) + s(Terminal) + s(S.F.Ratio) + 
                    s(perc.alumni) + s(Expend) + s(Grad.Rate), data = College.train)
  par(mfrow=c(3, 5))
  plot(model_gam)
  summary(model_gam)
  ## 正向影响显著的变量：Private、Apps、Accept、Top10perc、F.Undergrad、Room.Board、Personal、PhD、Terminal、S.F.Ratio、perc.alumni、Expend、Grad.Rate。
  ## 具有非线性影响的变量：Accept、Personal、S.F.Ratio、Expend。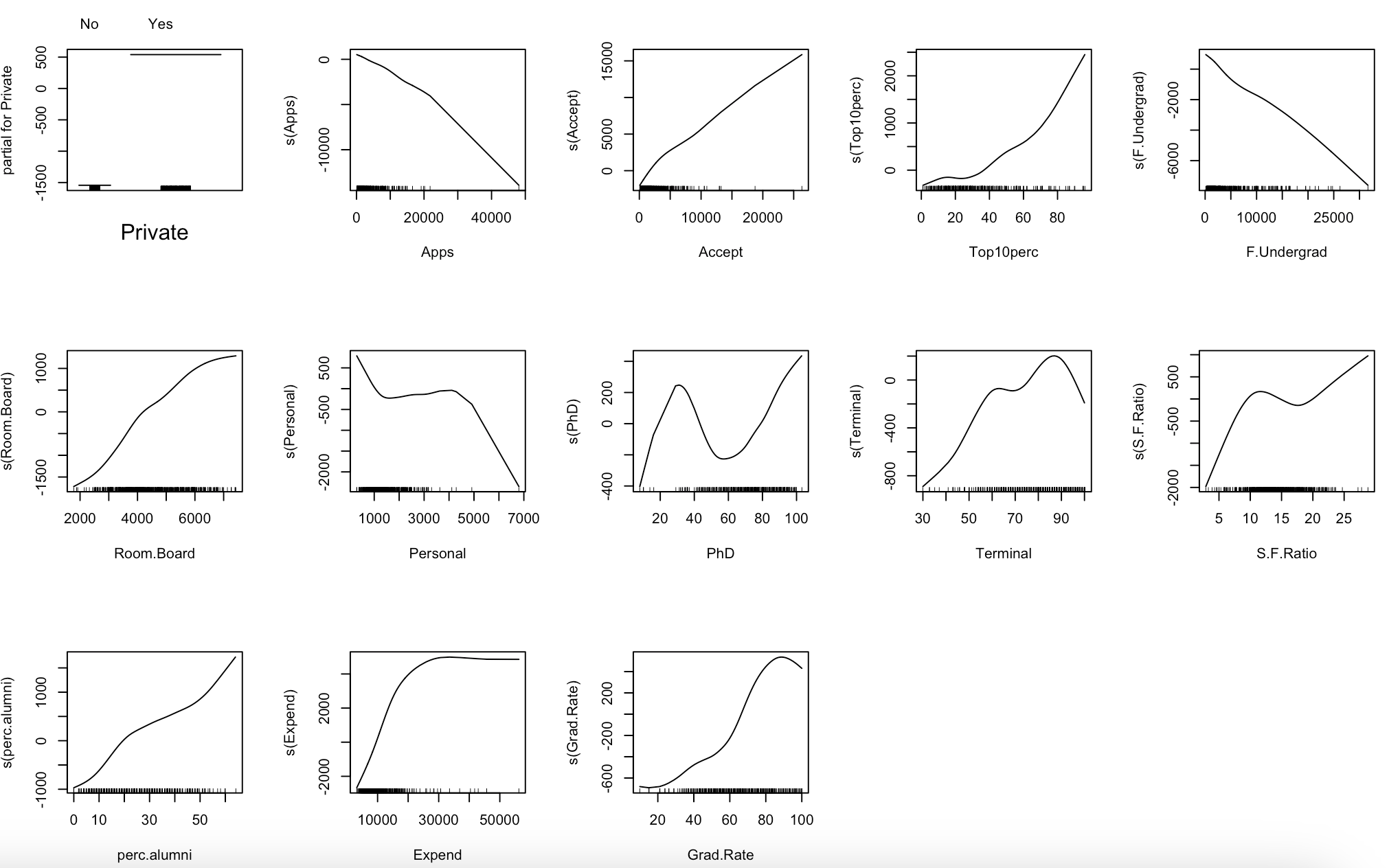
  

  

  

  

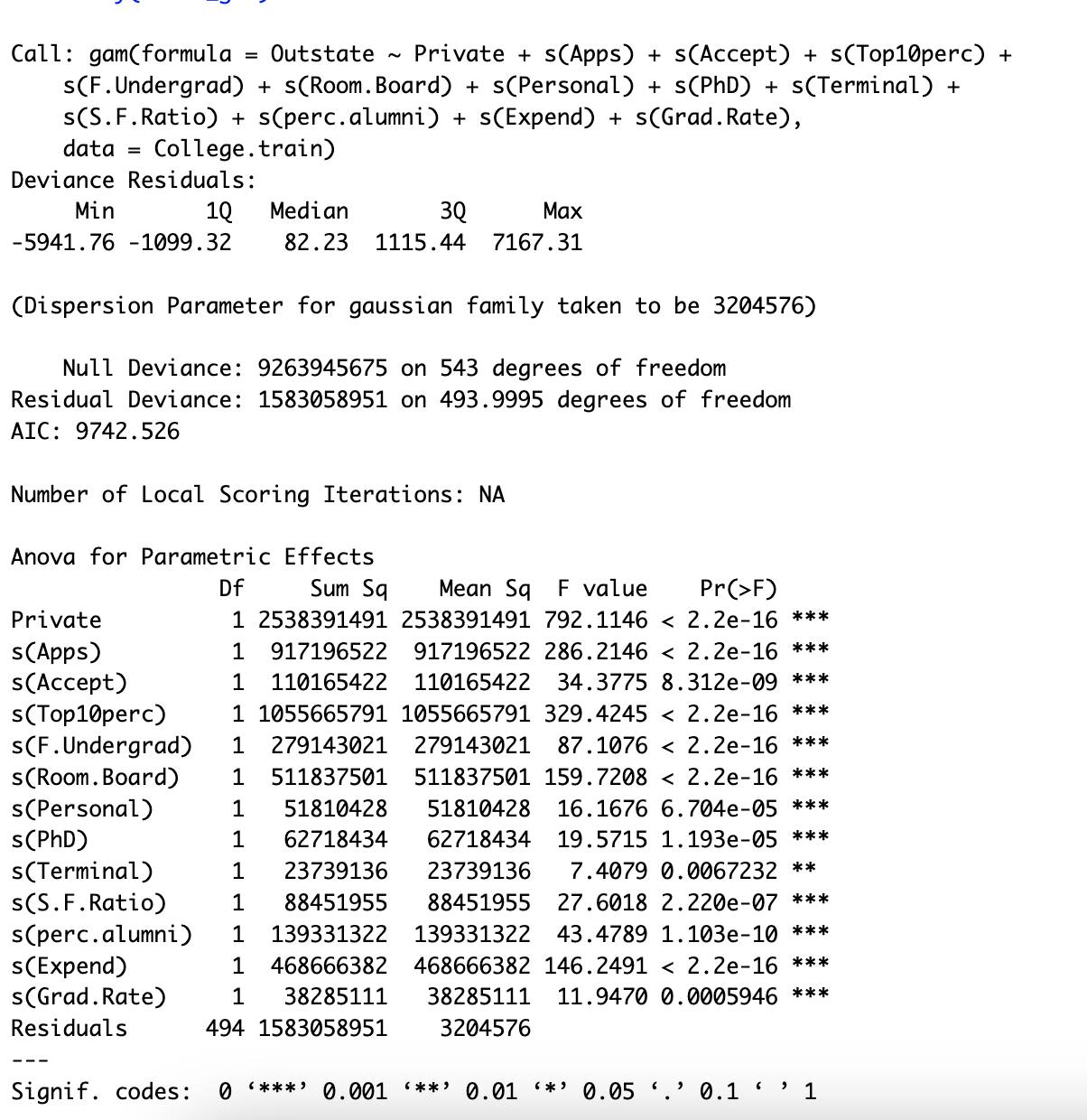
• (c)

  # 10.(c)
  gam.pred = predict(model_gam, College.test)
  gam.mse = mean((College.test$Outstate - gam.pred) ^ 2)
  print(paste("测试集均方误差 (MSE):", round(gam.mse, 2)))
  

  

• (d)

  # 10.(d)
  ## 如(b)中，具有非线性影响的变量：Accept、Personal、S.F.Ratio、Expend。
  

• 完整代码

  # 10.(a)
  library(ISLR)
  set.seed(1) 
  n = nrow(College) ## 数据总数
  p = ncol(College) - 1 ## 最大维度
  train = sample(1:n, size=round(0.7*n))
  College.train = College[train, ]
  College.test = College[-train, ]
  library(leaps)
  model_forward = regsubsets(Outstate~., data=College.train, nvmax=p, method="forward")
  model_forward_summary = summary(model_forward)
  par(mfrow=c(2,2))
  plot(1:p, model_forward_summary$cp, xlab="Degree", ylab="Cp", type="o")
  points(which.min(model_forward_summary$cp), min(model_forward_summary$cp), col="red", pch=16)
  plot(1:p, model_forward_summary$bic, xlab="Degree", ylab="BIC", type="o")
  points(which.min(model_forward_summary$bic), min(model_forward_summary$bic), col="red", pch=16)
  plot(1:p, model_forward_summary$adjr2, xlab="Degree", ylab="AdjR2", type="o")
  points(which.max(model_forward_summary$adjr2), max(model_forward_summary$adjr2), col="red", pch=16)
  ## 根据图像可以得出模型大小为13的时候效果最好
  coef(model_forward, 13)
  ## 可以看出包含如列表的13个变量，系数如下
  
  # 10.(b)
  library(gam)
  model_gam = gam(Outstate ~ Private + s(Apps) + s(Accept) + s(Top10perc) + s(F.Undergrad) + 
                    s(Room.Board) + s(Personal) + s(PhD) + s(Terminal) + s(S.F.Ratio) + 
                    s(perc.alumni) + s(Expend) + s(Grad.Rate), data = College.train)
  par(mfrow=c(3, 5))
  plot(model_gam)
  summary(model_gam)
  ## 正向影响显著的变量：Private、Apps、Accept、Top10perc、F.Undergrad、Room.Board、Personal、PhD、Terminal、S.F.Ratio、perc.alumni、Expend、Grad.Rate。
  ## 具有非线性影响的变量：Accept、Personal、S.F.Ratio、Expend。
  
  # 10.(c)
  gam.pred = predict(model_gam, College.test)
  gam.mse = mean((College.test$Outstate - gam.pred) ^ 2)
  print(paste("测试集均方误差 (MSE):", round(gam.mse, 2)))
  
  # 10.(d)
  ## 如(b)中，具有非线性影响的变量：Accept、Personal、S.F.Ratio、Expend。
  

7.9.11

• (a)

  # 11.(a)
  set.seed(1)
  x1 = rnorm(100)
  x2 = rnorm(100)
  eps = rnorm(100, 0.3)
  y = -5 + 1*x1 + 3*x2 + eps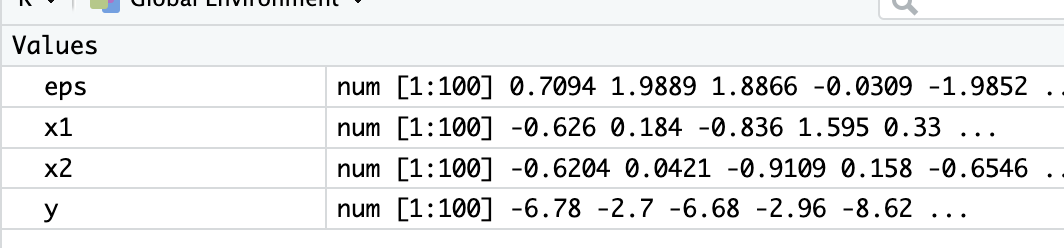
  

  

• (b)

  # 11.(b)
  beta1 = 3.14
  

• (c)

  # 11.(c)
  beta1 = 3.14
  a = y-beta1*x1
  beta2 = lm(a~x2)$coef[2]
  beta2
  

  

• (d)

  # 11.(d)
  a = y-beta2*x2
  beta1 = lm(a~x1)$coef[2]
  beta1
  

  

• (e)

  # 11.(e)
  b1 = rep(NA, 1000)
  b2 = rep(NA, 1000)
  b0 = rep(NA, 1000)
  b1[1] = 3.14
  for(i in 1:1000) {
    a = y-b1[i]*x1
    b2[i] = lm(a~x2)$coef[2]
    b = y-b2[i]*x2
    b1[i+1] = lm(b~x1)$coef[2]
    b0[i] = lm(b~x1)$coef[1]
    print(paste0("i=", i, " b0=", b0[i], " b1=", b1[i], " b2=", b2[i]))
  }
  b1 = b1[-(1001)]
  par(mfrow=c(1,1))
  plot(1:1000, b0, type="l", xlab="iterations", ylab="betas", ylim=c(-5,3), col="green", lwd=2)
  lines(1:1000, b1, col="blue", lwd=2)  # 添加 b1 的线，蓝色
  lines(1:1000, b2, col="red", lwd=2)   # 添加 b2 的线，红色
  legend("center", c("beta0","beta1","beta2"), lty=1, lwd=2, col=c("green","blue","red"))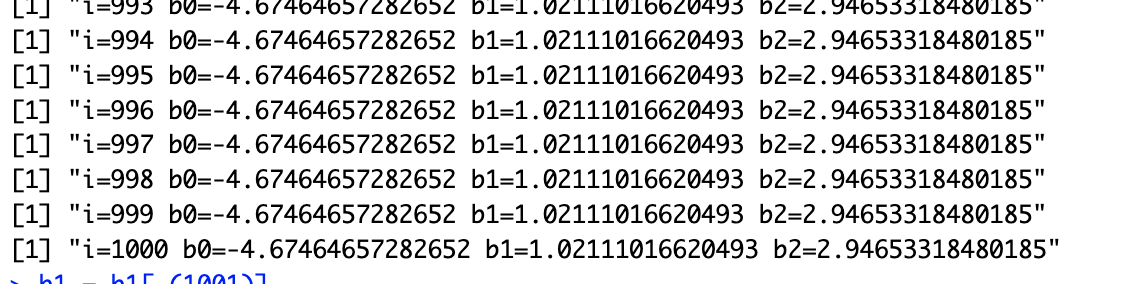
  

  

  

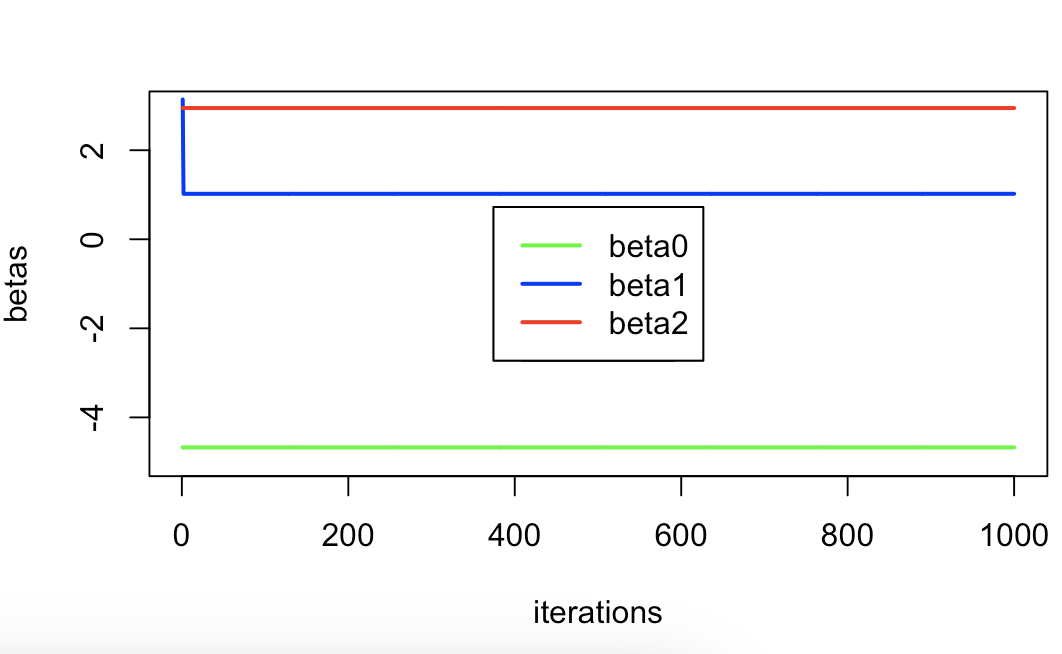
• (f)

  # 11.(f)
  model = lm(y~x1+x2)
  print(model$coef)
  print(paste0(" b0=", b0[1000], " b1=", b1[1000], " b2=", b2[1000]))
  abline(h=model$coef[1], lty="dashed", lwd=2)
  abline(h=model$coef[2], lty="dashed", lwd=2)
  abline(h=model$coef[3], lty="dashed", lwd=2)
  legend("center", c("beta0","beta1","beta2", "lm"), lty=c(1,1,1,3), lwd=2, col=c("green","blue","red","black"))
  

  

  

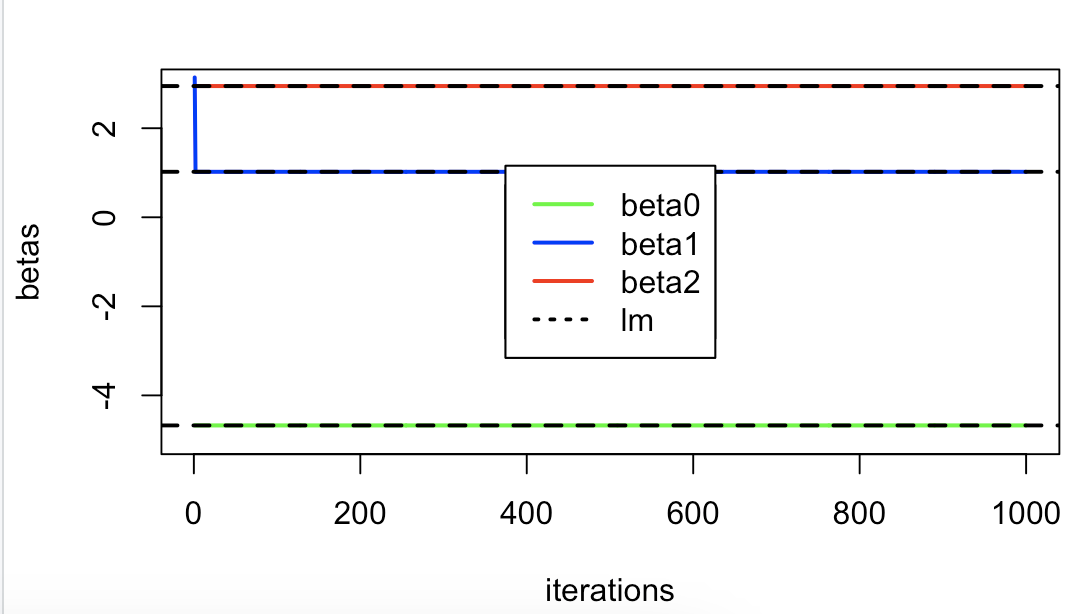
• (g)

  # 11.(g)
  ## 若预测变量与响应变量之间承线性关系，那么少量次数的迭代（1-20次）就可以使参数接近真实值
  

• 完整代码

  # 11.(a)
  set.seed(1)
  x1 = rnorm(100)
  x2 = rnorm(100)
  eps = rnorm(100, 0.3)
  y = -5 + 1*x1 + 3*x2 + eps
  
  # 11.(b)
  beta1 = 3.14
  
  # 11.(c)
  a = y-beta1*x1
  beta2 = lm(a~x2)$coef[2]
  beta2
  
  # 11.(d)
  a = y-beta2*x2
  beta1 = lm(a~x1)$coef[2]
  beta1
  
  # 11.(e)
  b1 = rep(NA, 1000)
  b2 = rep(NA, 1000)
  b0 = rep(NA, 1000)
  b1[1] = 3.14
  for(i in 1:1000) {
    a = y-b1[i]*x1
    b2[i] = lm(a~x2)$coef[2]
    b = y-b2[i]*x2
    b1[i+1] = lm(b~x1)$coef[2]
    b0[i] = lm(b~x1)$coef[1]
    print(paste0("i=", i, " b0=", b0[i], " b1=", b1[i], " b2=", b2[i]))
  }
  b1 = b1[-(1001)]
  par(mfrow=c(1,1))
  plot(1:1000, b0, type="l", xlab="iterations", ylab="betas", ylim=c(-5,3), col="green", lwd=2)
  lines(1:1000, b1, col="blue", lwd=2)  # 添加 b1 的线，蓝色
  lines(1:1000, b2, col="red", lwd=2)   # 添加 b2 的线，红色
  legend("center", c("beta0","beta1","beta2"), lty=1, lwd=2, col=c("green","blue","red"))
  
  # 11.(f)
  model = lm(y~x1+x2)
  print(model$coef)
  print(paste0(" b0=", b0[1000], " b1=", b1[1000], " b2=", b2[1000]))
  abline(h=model$coef[1], lty="dashed", lwd=2)
  abline(h=model$coef[2], lty="dashed", lwd=2)
  abline(h=model$coef[3], lty="dashed", lwd=2)
  legend("center", c("beta0","beta1","beta2", "lm"), lty=c(1,1,1,3), lwd=2, col=c("green","blue","red","black"))
  
  # 11.(g)
  ## 若预测变量与响应变量之间承线性关系，那么少量次数的迭代（1-20次）就可以使参数接近真实值