本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为4.7节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

4.7.1

image-20241014131931728

4.7.2

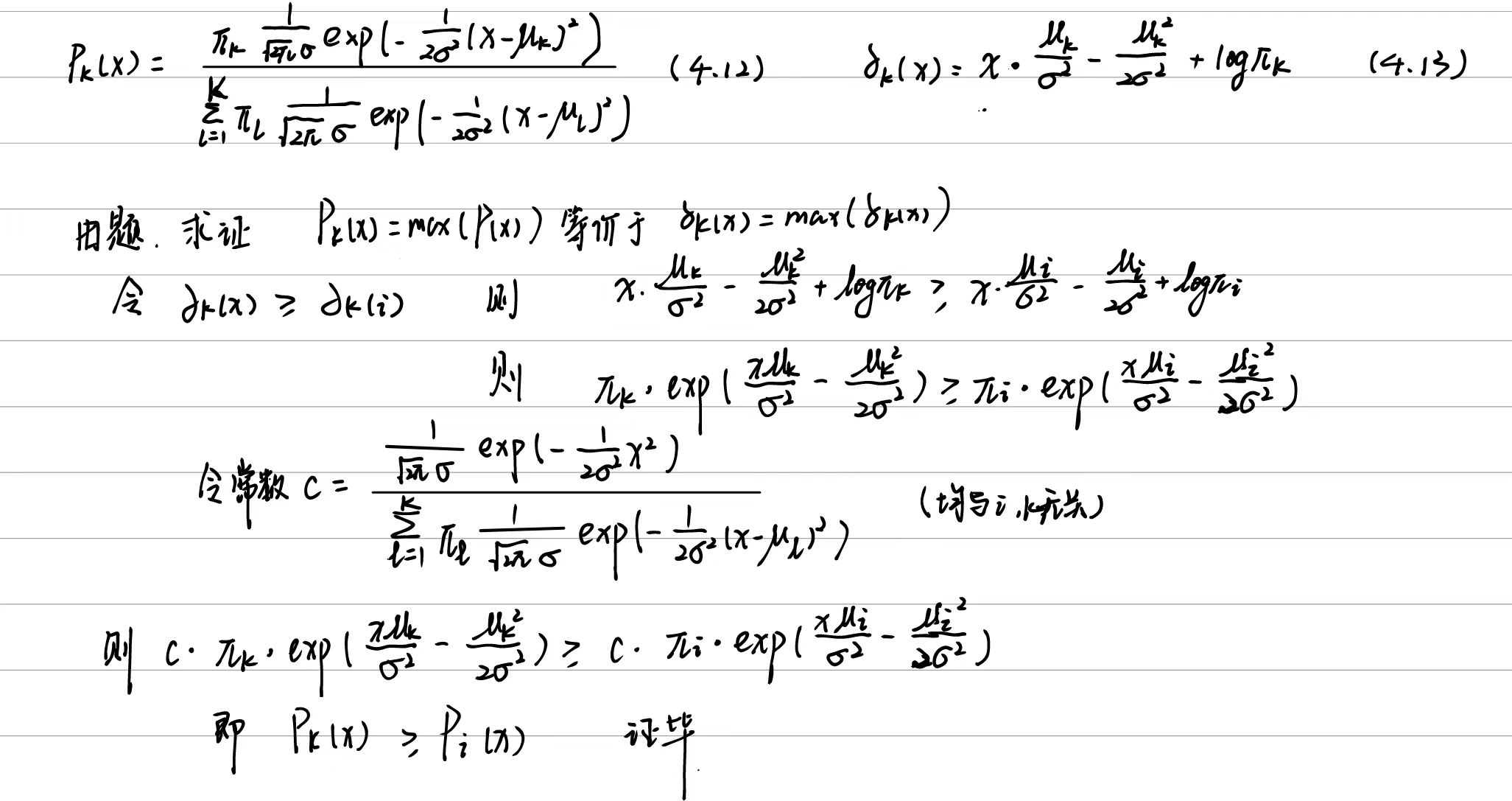
image-20241014150227226

4.7.4

  • (a)

    • 当观测点落在[0.05, 0.95]当中时，我们可以取X附近10%的范围区间（即[X-0.05, X+0.05]）内的训练观测用于预测。这部分来看预测模型需要观测中10%的数据（区间长度为0.1，即10%*1）。

    • 但是当观测点落在[0, 0.05)或者(0.95, 1]之间，会有一边到达临界（例如X=0.03， 那么抽取训练观测范围区间为[0, 0.8]）。那么这部分平均长度为(0.05+0.1)/2=0.075，所以这部分平均需要观测中为7.5%。

    • 总的来说，如果忽略边界情况，那么预测模型需要训练观测中10%的数据；如果不忽略边界情况，预测模型需要训练观测的比例为0.9*10\%+0.1*7.5\%=9.75\%。

  • (b)

    相对于(a)题变成了二维的情况。假设两个变量X1，X2相互独立，那么在不考虑边界情况的情况下，预测对于X1来说需要观测中10%的数据，对于X2来说也需要观测中10%的数据。那么满足落在测试的观测点10%范围内，则需要两个情况同时满足，则10\%*10\%=1\%。

  • (c)

    当把(a)、(b)推广到100维度，那么所需要的观测数据比例为(1\%)^{100}，即(0.1)^{100}。

  • (d)

    随着维度(p)的增加，p维度上出现接近测试观测点的训练观测点（即出现邻居）的概率（也就是前面说的观测数据比例）为\lim_{p->∞} (0.1)^p=0。那么也就是说明当p增加的时候，出现邻居的可能几乎为0，那么也就说明被迫选择的训练观测并不真正接近测试观测，导致模型效果很差。

  • (e)

    由题，超立方体的体积需要站总空间体积的10%，给出的总空间体积为1。 那么设超立方体每边边长为l，那么体积为l^p。即l^p=1*10\%=0.1。由此我们得到l=(0.1)^{1/p}。

    对于p=1的情况，l=(0.1)^{1}。

    对于p=2的情况，l=(0.1)^{1/2}。

    对于p=100的情况，l=(0.1)^{1/100}。

4.7.5

  • LDA：线性判别分析，假设每个类别的数据点服从多元正态分布，并且所有类别共享相同的协方差矩阵。目标是找到一个线性判别边界来划分不同类别。

  • QDA：二次判别分析，假设每个类别的数据点都服从多元正态分布，但是每个类别都有不同的协方差矩阵。目标是找到一个二次判别边界来划分不同类别。

  • (a)

    如果贝叶斯决策边界是非线性的，特别是在决策边界为二次的或者接近二次的情况下，情况如下：

    在训练集上，QDA效果更好。因为相对于LDA，QDA的灵活性更高，对数据拟合效果更好。

    在测试集上，LDA效果更好。因为贝叶斯决策边界为线性，而LDA进行判别分析也是找到现行的判别边界，LDA会更接近实际情况。而QDA可能出现过拟合的情况导致在测试集上效果不好。

  • (b)

    在训练集上，QDA效果更好。因为相对于LDA，QDA的灵活性更高，对数据拟合效果更好。

    再测试集上，QDA效果更好。因为贝叶斯决策边界为非线性，QDA灵活性更高也更符合实际情况。而LDA更适合线性情况。

  • (c)

    在样本量n增大时，LDA和QDA的预测率都会上升。但是相比于LDA，QDA会回变得更好。原因是在样本量比较小的时候，使用QDA可能会出现过拟合导致模型表现较差，但是当样本量增加，过拟合的概率有所降低，而QDA的灵活性相对于LDA更高，拟合情况和预测情况都会比LDA效果更好。

  • (d)

    错误。因为贝叶斯决策边界是现行的，那么选用LDA会更符合实际的情况。相对于LDA来说，QDA虽然可以表示线性边界，但是会引入不必要的复杂性，导致过拟合等问题出现，导致更大的方差，特别是在样本量比较小的情况下。针对于贝叶斯决策边界为线性的情况，仍应该选择LDA。

4.7.6

image-20241014170103191

4.7.8

在1最近邻法中，每个数据点的预测类别是根据在训练集中最近的1个邻居决定的。而在训练集中，由于每个点都是自己最近的邻居，那么使用训练集对模型预测的结果必然是正确的，也就是说明K=1的KNN在训练集中错误率为0%。

根据上述情况，又因为K=1的KNN方法的平均错误率为18%，而训练集和测试集的数据量相同，那么说明该方法在测试集上的平均错误率为36%。

对于新的数据来说，逻辑斯蒂回归在测试集上的错误率为30%，而使用K=1的KNN方法在测试集上的错误率为36%，所以采取逻辑斯蒂回归的分类方法效果会更好。

4.7.9

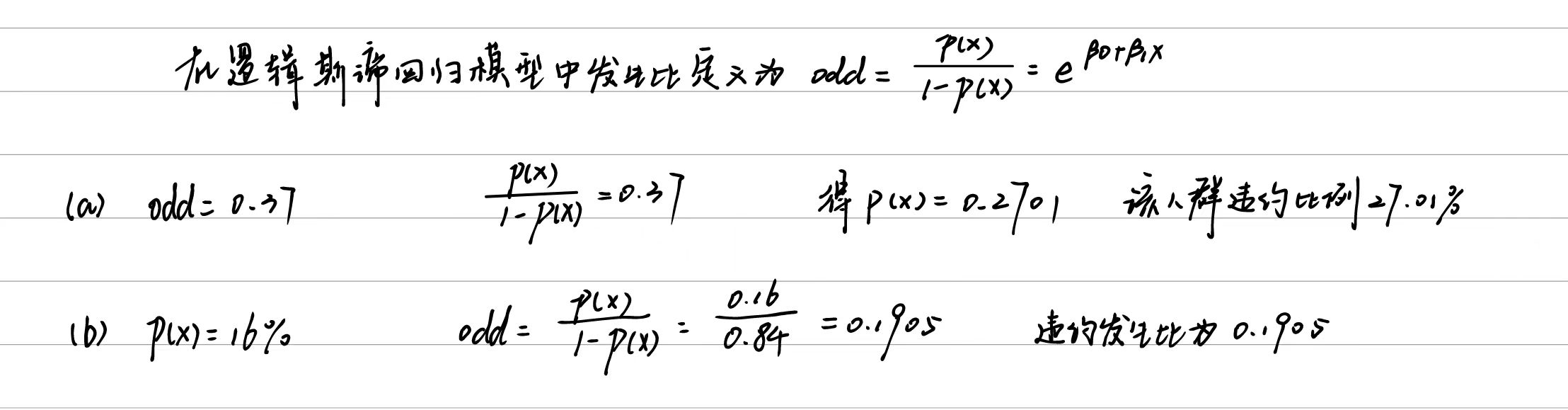
image-20241015124956418

二、应用题

4.7.10

  • (a)

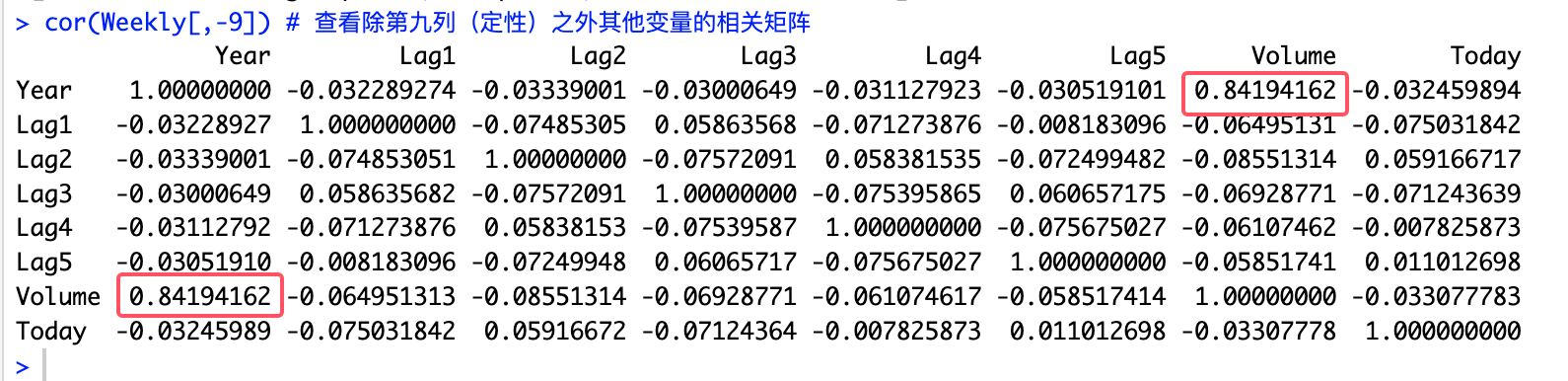
    # 10.(a)
library(ISLR)
Weekly
summary(Weekly) # 查看数据总结
pairs(Weekly) # 查看散点图
cor(Weekly[,-9]) # 查看除第九列（定性）之外其他变量的相关矩阵
## 从散点图当中可以看出Volume和Year有很强的关系
## 在相关矩阵中二者相关系数达到0.8419也说明有很强关系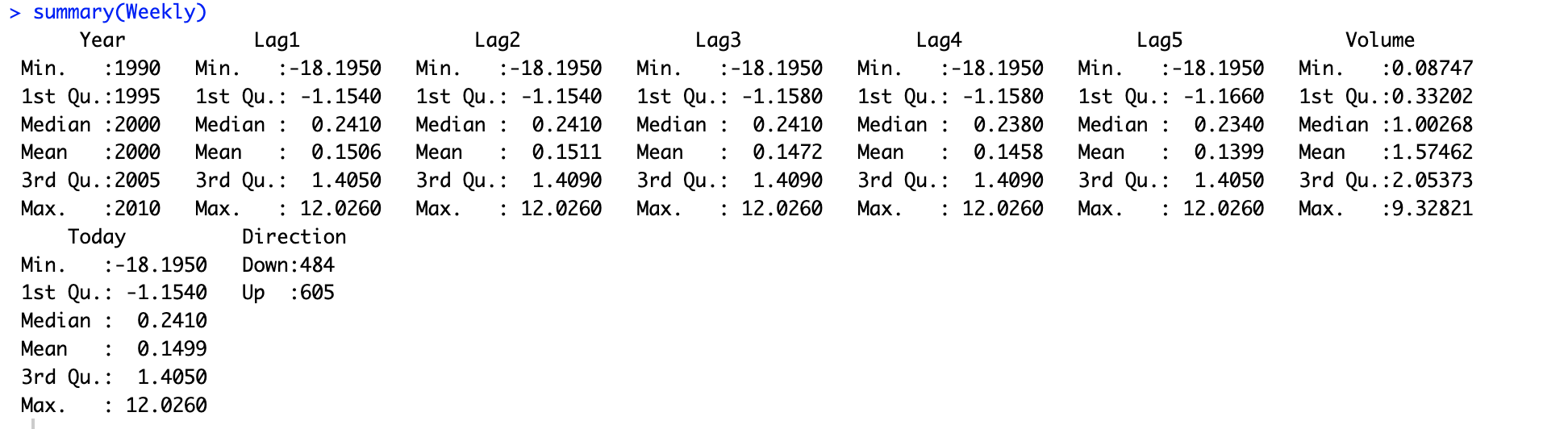

    image-20241015130224937

    QQ_1728969076428

    QQ_1728969137999

  • (b)

    # 10.(b)
glm.fit = glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume, data=Weekly, family = binomial)
## family = binomial表示响应变量的数据类型为二项分布，适用于逻辑斯蒂回归等二分类问题
summary(glm.fit)
## 在输出的结果当中，发现只有Lag2的p值<0.05可以拒绝零假设认为与响应变量之间有显著关系

    QQ_1728969916834

  • (c)

    # 10.(c)
glm.probs = predict(glm.fit, type="response") # 生成模型的预测值，response为指定返回预测的概率而不是类别
glm.pred = rep("Down", length(glm.probs)) # 创建一个向量值为"Down"，长度与glm.probs相同
glm.pred[glm.probs > 0.5] = "Up" # 将概率>0.5的视为“Up”
table(glm.pred, Weekly$Direction) # 创建一个混淆矩阵，将glm.pred与Direction进行比较
## 整体预测准确率:(54+557)/(54+48+430+557)=0.561
## 真阳性率:(557)/(557+48)=0.92 假阳性率:(430)/(430+54)=0.888
## 真阴性率:(54)/(54+430)=0.112 假阴性率:(48)/(48+557)=0.079
## 假阳性出现了430次，概率为88.8% 将实际的Down判断为了Up
## 假阴性出现了48次，概率为7.9% 将实际的Up判断为了Down

    QQ_1728970835295

  • (d)

    # 10.(d)
train = subset(Weekly, Year<=2008) # 划分训练集
test = subset(Weekly， Year >= 2009) # 划分测试集
glm.fit.2 = glm(Direction~Lag2, data=train, family=binomial) # 使用训练集训练逻辑斯蒂回归模型
glm.probs.2 = predict(glm.fit.2, type="response", test) # 使用训练好的模型根据测试集预测
glm.pred.2 = rep("Down", length(glm.probs.2))
glm.pred.2[glm.probs.2>0.5] = "Up"
table(glm.pred.2, test$Direction) # 列出混淆矩阵
mean(glm.pred.2==test$Direction) # 列出总体预测准确率 62.5%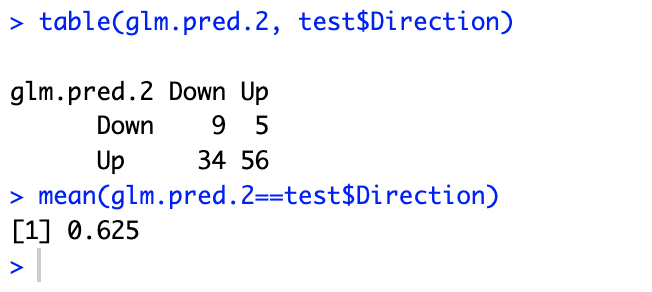

    QQ_1728971906226

  • (e)

    # 10.(e)
library(MASS)
lda.fit = lda(Direction~Lag2, data=train)
lda.pred = predict(lda.fit, test) # 通过lda.fit模型预测类别
table(lda.pred$class, test$Direction) # 混淆矩阵
mean(lda.pred$class==test$Direction) # 总体预测准确率 62.5%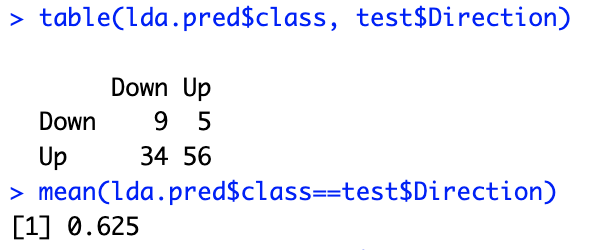

    QQ_1728972523779

  • (f)

    # 10.(f)
qda.fit = qda(Direction~Lag2, data=train)
qda.pred = predict(qda.fit, test) # 通过qda.fit模型预测类别
table(qda.pred$class, test$Direction) # 混淆矩阵
mean(qda.pred$class==test$Direction) # 总体预测准确率 58.65%

    QQ_1728972628404

  • (g)

    # 10.(g)
library(class)
train.KNN = as.matrix(Weekly$Lag2[Weekly$Year<=2008]) # 将2008年及之前的Lag2列转换为矩阵作为训练集
test.KNN = as.matrix(Weekly$Lag2[Weekly$Year>=2009]) # 将2009年及之后的Lag2列转换为矩阵作为测试集
trainlabel.KNN = Weekly$Direction[Weekly$Year<=2008] # 获取训练集标签
testlabel.KNN = Weekly$Direction[Weekly$Year>=2009] # 获取测试集标签
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=1) # 通过K=1的KNN算法进行预测
table(knn.pred, testlabel.KNN) # 混淆矩阵
mean(knn.pred == testlabel.KNN) # 预测准确率 50%

    QQ_1728973230728

  • (h)

    # 10.(h)
## glm的准确率和lda准确率都为62.5%表现最好
## qda准确率为58.65% knn(k=1)准确率为50%

  • (i)

    # 10.(i)
### glm
glm.fit = glm(Direction ~ Volume+Lag2+Volume:Lag2, data=train, family=binomial)
summary(glm.fit)
glm.probs = predict(glm.fit, test)
glm.pred = ifelse(glm.probs>0.5, "Up", "Down")
table(glm.pred, test$Direction)
mean(glm.pred == test$Direction)
## 使用Volume和Lag2的glm预测，结果准确率为42.31%
glm.fit = glm(Direction ~ Lag2+sqrt(abs(Lag2))+I(Lag2^2)+log(abs(Lag2)), data=train, family=binomial)
summary(glm.fit)
glm.probs = predict(glm.fit, test)
glm.pred = ifelse(glm.probs>0.5, "Up", "Down")
table(glm.pred, test$Direction)
mean(glm.pred == test$Direction)
## 使用Lag2的变换进行glm预测，准确率为48.07%
### lda
lda.fit = lda(Direction ~ Lag2+sqrt(abs(Lag2))+I(Lag2^2)+log(abs(Lag2)), data=train)
lda.pred = predict(lda.fit, test)
table(lda.pred$class, test$Direction) # 混淆矩阵
mean(lda.pred$class==test$Direction) # 总体预测准确率 58.65%
### qda
qda.fit = qda(Direction ~ Lag2+sqrt(abs(Lag2))+I(Lag2^2)+log(abs(Lag2)), data=train)
qda.pred = predict(qda.fit, test)
table(qda.pred$class, test$Direction) # 混淆矩阵
mean(qda.pred$class==test$Direction) # 总体预测准确率 57.69%
### KNN
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=10)
table(knn.pred, testlabel.KNN)
mean(knn.pred == testlabel.KNN) # k=10
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=50)
table(knn.pred, testlabel.KNN)
mean(knn.pred == testlabel.KNN) # k=50
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=100)
table(knn.pred, testlabel.KNN)
mean(knn.pred == testlabel.KNN) # k=100

    QQ_1728974130182

    QQ_1728974364455

    QQ_1728974524756

    QQ_1728974623159

    QQ_1728974951052

  • 完整代码

    # 10.(a)
library(ISLR)
Weekly
summary(Weekly) # 查看数据总结
pairs(Weekly) # 查看散点图
cor(Weekly[,-9]) # 查看除第九列（定性）之外其他变量的相关矩阵
## 从散点图当中可以看出Volume和Year有很强的关系
## 在相关矩阵中二者相关系数达到0.8419也说明有很强关系
​
# 10.(b)
glm.fit = glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume, data=Weekly, family=binomial)
## family = binomial表示响应变量的数据类型为二项分布，适用于逻辑斯蒂回归等二分类问题
summary(glm.fit)
## 在输出的结果当中，发现只有Lag2的p值<0.05可以拒绝零假设认为与响应变量之间有显著关系
​
# 10.(c)
glm.probs = predict(glm.fit, type="response") # 生成模型的预测值，response为指定返回预测的概率而不是类别
glm.pred = rep("Down", length(glm.probs)) # 创建一个向量值为"Down"，长度与glm.probs相同
glm.pred[glm.probs > 0.5] = "Up" # 将概率>0.5的视为“Up”
table(glm.pred, Weekly$Direction) # 创建一个混淆矩阵，将glm.pred与Direction进行比较
## 整体预测准确率:(54+557)/(54+48+430+557)=0.561
## 真阳性率:(557)/(557+48)=0.92 假阳性率:(430)/(430+54)=0.888
## 真阴性率:(54)/(54+430)=0.112 假阴性率:(48)/(48+557)=0.079
## 假阳性出现了430次，概率为88.8% 将实际的Down判断为了Up
## 假阴性出现了48次，概率为7.9% 将实际的Up判断为了Down
​
# 10.(d)
train = subset(Weekly, Year<=2008) # 划分训练集
test = subset(Weekly, Year >= 2009) # 划分测试集
glm.fit.2 = glm(Direction~Lag2, data=train, family=binomial) # 使用训练集训练逻辑斯蒂回归模型
glm.probs.2 = predict(glm.fit.2, type="response", test) # 使用训练好的模型根据测试集预测
glm.pred.2 = rep("Down", length(glm.probs.2))
glm.pred.2[glm.probs.2>0.5] = "Up"
table(glm.pred.2, test$Direction) # 列出混淆矩阵
mean(glm.pred.2==test$Direction) # 列出总体预测准确率 62.5%
​
# 10.(e)
library(MASS)
lda.fit = lda(Direction~Lag2, data=train)
lda.pred = predict(lda.fit, test) # 通过lda.fit模型预测类别
table(lda.pred$class, test$Direction) # 混淆矩阵
mean(lda.pred$class==test$Direction) # 总体预测准确率 62.5%
​
# 10.(f)
qda.fit = qda(Direction~Lag2, data=train)
qda.pred = predict(qda.fit, test) # 通过qda.fit模型预测类别
table(qda.pred$class, test$Direction) # 混淆矩阵
mean(qda.pred$class==test$Direction) # 总体预测准确率 58.65%
​
# 10.(g)
library(class)
train.KNN = as.matrix(Weekly$Lag2[Weekly$Year<=2008]) # 将2008年及之前的Lag2列转换为矩阵作为训练集
test.KNN = as.matrix(Weekly$Lag2[Weekly$Year>=2009]) # 将2009年及之后的Lag2列转换为矩阵作为测试集
trainlabel.KNN = Weekly$Direction[Weekly$Year<=2008] # 获取训练集标签
testlabel.KNN = Weekly$Direction[Weekly$Year>=2009] # 获取测试集标签
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=1) # 通过K=1的KNN算法进行预测
table(knn.pred, testlabel.KNN) # 混淆矩阵
mean(knn.pred == testlabel.KNN) # 预测准确率 50%
​
# 10.(h)
## glm的准确率和lda准确率都为62.5%表现最好
## qda准确率为58.65% knn(k=1)准确率为50%
​
# 10.(i)
### glm
glm.fit = glm(Direction ~ Volume+Lag2+Volume:Lag2, data=train, family=binomial)
summary(glm.fit)
glm.probs = predict(glm.fit, test)
glm.pred = ifelse(glm.probs>0.5, "Up", "Down")
table(glm.pred, test$Direction)
mean(glm.pred == test$Direction)
## 使用Volume和Lag2的glm预测，结果准确率为42.31%
glm.fit = glm(Direction ~ Lag2+sqrt(abs(Lag2))+I(Lag2^2)+log(abs(Lag2)), data=train, family=binomial)
summary(glm.fit)
glm.probs = predict(glm.fit, test)
glm.pred = ifelse(glm.probs>0.5, "Up", "Down")
table(glm.pred, test$Direction)
mean(glm.pred == test$Direction)
## 使用Lag2的变换进行glm预测，准确率为48.07%
### lda
lda.fit = lda(Direction ~ Lag2+sqrt(abs(Lag2))+I(Lag2^2)+log(abs(Lag2)), data=train)
lda.pred = predict(lda.fit, test)
table(lda.pred$class, test$Direction) # 混淆矩阵
mean(lda.pred$class==test$Direction) # 总体预测准确率 58.65%
### qda
qda.fit = qda(Direction ~ Lag2+sqrt(abs(Lag2))+I(Lag2^2)+log(abs(Lag2)), data=train)
qda.pred = predict(qda.fit, test)
table(qda.pred$class, test$Direction) # 混淆矩阵
mean(qda.pred$class==test$Direction) # 总体预测准确率 57.69%
### KNN
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=10)
table(knn.pred, testlabel.KNN)
mean(knn.pred == testlabel.KNN) # k=10
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=50)
table(knn.pred, testlabel.KNN)
mean(knn.pred == testlabel.KNN) # k=50
knn.pred = knn(train.KNN, test.KNN, trainlabel.KNN, k=100)
table(knn.pred, testlabel.KNN)
mean(knn.pred == testlabel.KNN) # k=100

4.7.11

  • (a)

    # 11.(a)
library(ISLR)
attach(Auto)
mpg01 = rep(0, length(mpg)) # 创建mpg01向量，默认为0，长度等同于mpg
mpg01[mpg>median(mpg)] = 1 # mpg中大于中位数的mpg01值设置为1
Auto=data.frame(Auto, mpg01) # 合并成新数据集

  • (b)

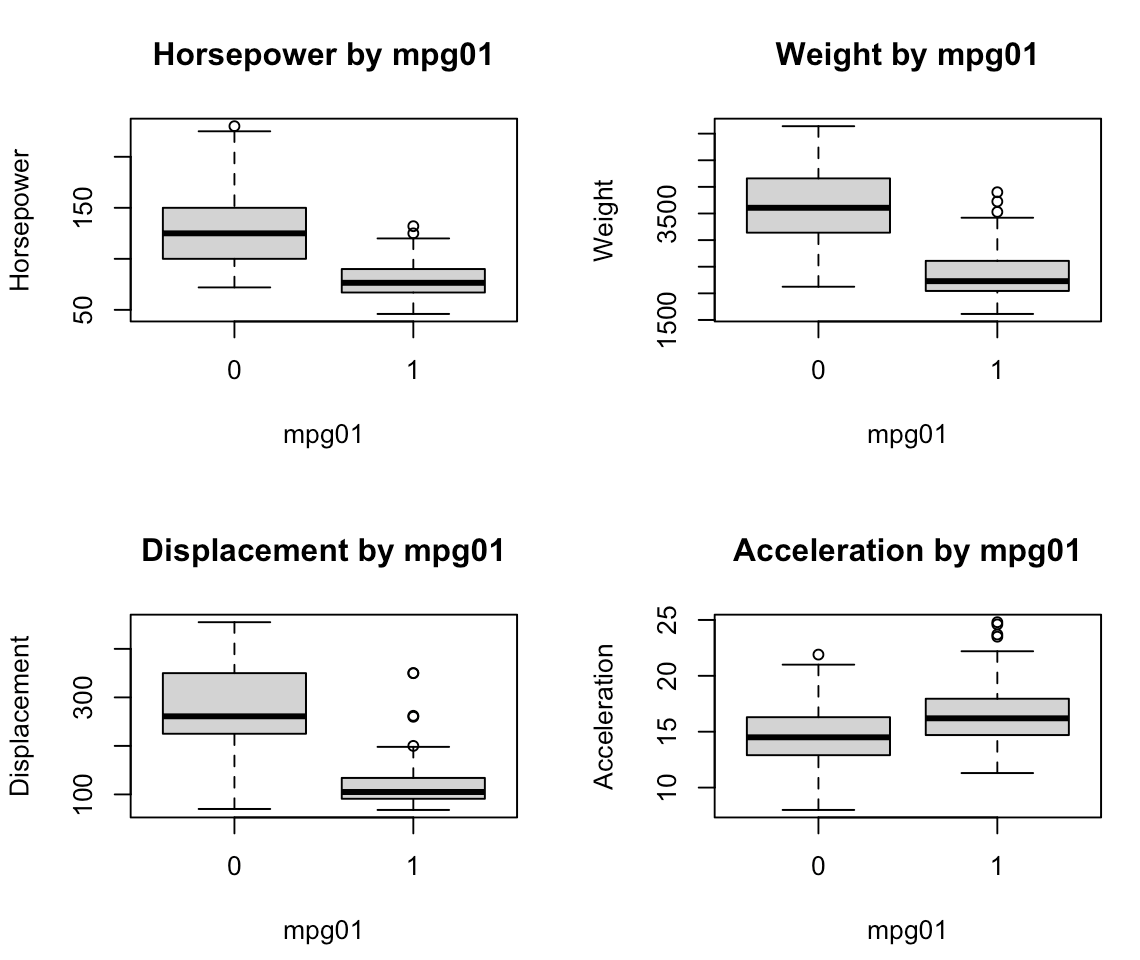
    # 11.(b)
pairs(Auto)
## 根据散点图可以看出除了mpg外，displacement、horsepower、weight、acceleration与mpg01存在关系
par(mfrow=c(2, 2))
boxplot(Auto$horsepower ~ mpg01, xlab="mpg01", ylab="Horsepower", main="Horsepower by mpg01")
boxplot(Auto$weight ~ Auto$mpg01, xlab="mpg01", ylab="Weight", main="Weight by mpg01")
boxplot(Auto$displacement ~ Auto$mpg01, xlab="mpg01", ylab="Displacement", main="Displacement by mpg01")
boxplot(Auto$acceleration ~ Auto$mpg01, xlab="mpg01", ylab="Acceleration", main="Acceleration by mpg01")
## Horsepower:随着马力增加，mpg01更可能为0（马力较大的汽车油耗较高，mpg每加仑汽油行驶的公里数较低）
## Weight:随着重量增加，mpg01更可能为0（重量大的汽车油耗较高）
## Displacement:随着排量增加，mpg01更可能为0（排量大的汽车油耗高）
## Acceleration:可以看出加速度与mpg01的关系并不明显

    QQ_1728976621248

    QQ_1728976862143

  • (c)

    # 11.(c)
median(Auto$year) # 获取年份中位数76作为划分条件
train = subset(Auto, year<=76) # 训练集
test = subset(Auto, year>76) # 测试集
test.mpg01 = mpg01[year>76] # 测试集的mpg01

    image-20241015165533925

  • (d)

    # 11.(d)
library(MASS)
lda.fit=lda(mpg01~horsepower+weight+displacement+cylinders, data=train)
lda.pred=predict(lda.fit, test)
table(lda.pred$class, test.mpg01)
mean(lda.pred$class != test.mpg01) # 测试集上的误差为(13+6=19)，测试误差率为10.67%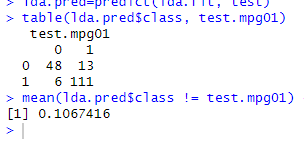

    image-20241015170654413

  • (e)

    # 11.(e)
qda.fit=qda(mpg01~horsepower+weight+displacement+cylinders, data=train)
qda.pred=predict(qda.fit, test)
table(qda.pred$class, test.mpg01)
mean(qda.pred$class != test.mpg01) # 测试集上的误差为(20+4=24)，测试误差率为13.48%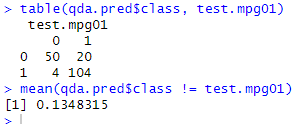

    image-20241015171033514

  • (f)

    # 11.(f)
glm.fit=glm(mpg01~horsepower+weight+displacement+cylinders, data=train, family=binomial)
glm.probs=predict(glm.fit, test)
glm.pred=ifelse(glm.probs>0.5, 1, 0)
table(glm.pred, test.mpg01)
mean(glm.pred != test.mpg01) # 测试集上的误差为(40)，测试误差率为22.47%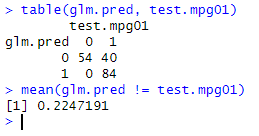

    image-20241015171927993

  • (g)

    # 11.(g)
train.KNN = cbind(train$cylinders, train$displacement, train$horsepower, train$weight) # 训练集（cbind按列合并）
test.KNN = cbind(test$cylinders, test$displacement, test$horsepower, test$weight) # 测试集
train.mpg01.KNN = train$mpg01 # 训练集mpg01
test.mpg01.KNN = test$mpg01 # 测试集mpg01
library(class)
### K=1
knn.pred.1=knn(train.KNN, test.KNN, train.mpg01.KNN, k=1)
table(knn.pred.1, test.mpg01.KNN)
mean(knn.pred.1 != test.mpg01.KNN)
### k=10
knn.pred.10=knn(train.KNN, test.KNN, train.mpg01.KNN, k=10)
table(knn.pred.10, test.mpg01.KNN)
mean(knn.pred.10 != test.mpg01.KNN)
### k=50
knn.pred.50=knn(train.KNN, test.KNN, train.mpg01.KNN, k=50)
table(knn.pred.50, test.mpg01.KNN)
mean(knn.pred.50 != test.mpg01.KNN)
### k=100
knn.pred.100=knn(train.KNN, test.KNN, train.mpg01.KNN, k=100)
table(knn.pred.100, test.mpg01.KNN)
mean(knn.pred.100 != test.mpg01.KNN)
## KNN的k=50误差率最低，效果最好

    image-20241015173029941

  • 完整代码

    # 11.(a)
library(ISLR)
attach(Auto)
mpg01 = rep(0, length(mpg)) # 创建mpg01向量，默认为0，长度等同于mpg
mpg01[mpg>median(mpg)] = 1 # mpg中大于中位数的mpg01值设置为1
Auto=data.frame(Auto, mpg01) # 合并成新数据集
​
# 11.(b)
pairs(Auto)
## 根据散点图可以看出除了mpg外，cylinders、displacement、horsepower、weight与mpg01存在关系
par(mfrow=c(2, 2))
boxplot(Auto$horsepower ~ mpg01, xlab="mpg01", ylab="Horsepower", main="Horsepower by mpg01")
boxplot(Auto$weight ~ Auto$mpg01, xlab="mpg01", ylab="Weight", main="Weight by mpg01")
boxplot(Auto$displacement ~ Auto$mpg01, xlab="mpg01", ylab="Displacement", main="Displacement by mpg01")
boxplot(Auto$cylinders ~ Auto$mpg01, xlab="mpg01", ylab="Cylinders", main="Cylinders by mpg01")
## Horsepower:随着马力增加，mpg01更可能为0（马力较大的汽车油耗较高，mpg每加仑汽油行驶的公里数较低）
## Weight:随着重量增加，mpg01更可能为0（重量大的汽车油耗较高）
## Displacement:随着排量增加，mpg01更可能为0（排量大的汽车油耗高）
## Cylinders:随着气缸数增加，mpg01更可能为0（气缸数多的汽车油耗高）
​
# 11.(c)
median(Auto$year) # 获取年份中位数76作为划分条件
train = subset(Auto, year<=76) # 训练集
test = subset(Auto, year>76) # 测试集
test.mpg01 = mpg01[year>76] # 测试集的mpg01
​
# 11.(d)
library(MASS)
lda.fit=lda(mpg01~horsepower+weight+displacement+cylinders, data=train)
lda.pred=predict(lda.fit, test)
table(lda.pred$class, test.mpg01)
mean(lda.pred$class != test.mpg01) # 测试集上的误差为(13+6=19)，测试误差率为10.67%
​
# 11.(e)
qda.fit=qda(mpg01~horsepower+weight+displacement+cylinders, data=train)
qda.pred=predict(qda.fit, test)
table(qda.pred$class, test.mpg01)
mean(qda.pred$class != test.mpg01) # 测试集上的误差为(20+4=24)，测试误差率为13.48%
​
# 11.(f)
glm.fit=glm(mpg01~horsepower+weight+displacement+cylinders, data=train, family=binomial)
glm.probs=predict(glm.fit, test)
glm.pred=ifelse(glm.probs>0.5, 1, 0)
table(glm.pred, test.mpg01)
mean(glm.pred != test.mpg01) # 测试集上的误差为(40)，测试误差率为22.47%
​
# 11.(g)
train.KNN = cbind(train$cylinders, train$displacement, train$horsepower, train$weight) # 训练集（cbind按列合并）
test.KNN = cbind(test$cylinders, test$displacement, test$horsepower, test$weight) # 测试集
train.mpg01.KNN = train$mpg01 # 训练集mpg01
test.mpg01.KNN = test$mpg01 # 测试集mpg01
library(class)
### K=1
knn.pred.1=knn(train.KNN, test.KNN, train.mpg01.KNN, k=1)
table(knn.pred.1, test.mpg01.KNN)
mean(knn.pred.1 != test.mpg01.KNN)
### k=10
knn.pred.10=knn(train.KNN, test.KNN, train.mpg01.KNN, k=10)
table(knn.pred.10, test.mpg01.KNN)
mean(knn.pred.10 != test.mpg01.KNN)
### k=50
knn.pred.50=knn(train.KNN, test.KNN, train.mpg01.KNN, k=50)
table(knn.pred.50, test.mpg01.KNN)
mean(knn.pred.50 != test.mpg01.KNN)
### k=100
knn.pred.100=knn(train.KNN, test.KNN, train.mpg01.KNN, k=100)
table(knn.pred.100, test.mpg01.KNN)
mean(knn.pred.100 != test.mpg01.KNN)
## KNN的k=50误差率最低，效果最好

4.7.12

  • (a)

    # 12.(a)
Power = function() {
  print(2^3) # 打印2的三次方
}
Power()

    image-20241015181528995

  • (b)

    # 12.(b)
Power2 = function(x,a) {
  print(x^a)
}
Power2(3, 8)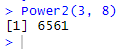

    image-20241015181639563

  • (c)

    # 12.(c)
Power2(10, 3)
Power2(8, 17)
Power2(131, 3)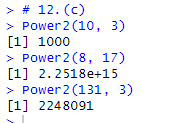

    image-20241015181837563

  • (d)

    # 12.(d)
Power3 = function(x,a) {
  result = x^a
  return(result)
}
print(Power3(3, 8))

    image-20241015182049174

  • (e)

    # 12.(e)
par(mfrow=c(2, 2))
x = 1:10
y = Power3(x,2)
## 绘制普通坐标轴（type：p-点,l-线,b-点和线段,c-线段,o-点和线段[连续],h-垂直线,s-阶梯线）
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像")
## 对数X轴
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像", log="x")
## 对数Y轴
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像", log="y")
## 对数XY轴
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像", log="xy")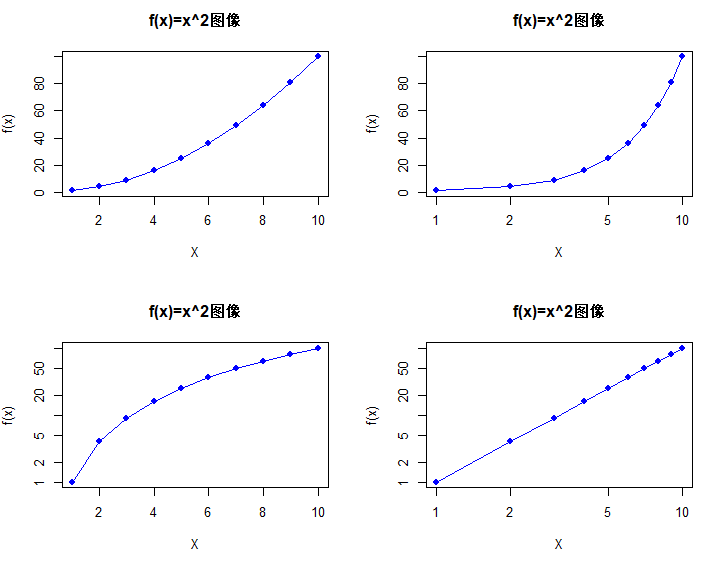

    image-20241015183626314

  • (f)

    # 12.(f)
PlotPower = function(x_range, a) {
  y_2 = x_range ^ a
  plot(x_range, y_2, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^a图像")
}
par(mfrow=c(1, 2))
PlotPower(1:10, 3)
PlotPower(-10:10, 2)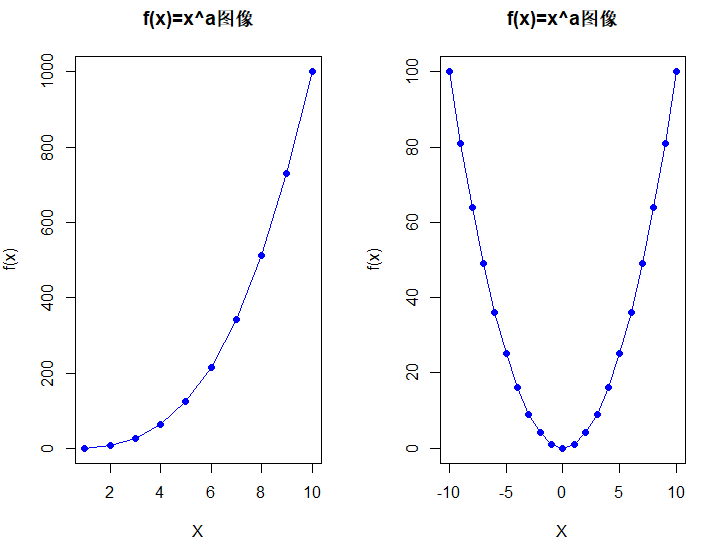

    image-20241015184346307

  • 完整代码

    # 12.(a)
Power = function() {
  print(2^3) # 打印2的三次方
}
Power()
​
# 12.(b)
Power2 = function(x,a) {
  print(x^a)
}
Power2(3, 8)
​
# 12.(c)
Power2(10, 3)
Power2(8, 17)
Power2(131, 3)
​
# 12.(d)
Power3 = function(x,a) {
  result = x^a
  return(result)
}
print(Power3(3, 8))
​
# 12.(e)
par(mfrow=c(2, 2))
x = 1:10
y = Power3(x,2)
## 绘制普通坐标轴（type：p-点,l-线,b-点和线段,c-线段,o-点和线段[连续],h-垂直线,s-阶梯线）
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像")
## 对数X轴
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像", log="x")
## 对数Y轴
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像", log="y")
## 对数XY轴
plot(x, y, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^2图像", log="xy")
​
# 12.(f)
PlotPower = function(x_range, a) {
  y_2 = x_range ^ a
  plot(x_range, y_2, type="o", col="blue", pch=19, xlab="X", ylab="f(x)", main="f(x)=x^a图像")
}
par(mfrow=c(1, 2))
PlotPower(1:10, 3)
PlotPower(-10:10, 2)
​