本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为5.4节、6.8节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

5.4.3

  • (a)

    K折交叉验证法通过将数据集多次拆分为训练集和测试集（验证集），从而提供更可靠的评估结果。下面是k折交叉验证法的步骤：

    1. 选定一个K值并将数据集随机分成K个大小尽可能相同的子集D_1, D_2, \dots, D_K。

    2. 每次选择其中一个子集D_i作为测试集，将其他的K-1个子集合并为训练集。并根据训练集进行模型的训练，根据测试集来评估模型性能。

    3. 最终根据K次训练与评估的结果取平均值作为对模型综合评估的结果。

  • (b)

    1. 验证集方法：将数据集随机划分为互相不重叠的训练集和测试集，并根据训练集训练，根据测试集评估性能。

      K折交叉验证相对于验证集优点：1. 多次拆分数据集并进行训练和验证，减少了由于单次拆分所造成的偏差；2. 数据集中的每一条数据都既用作训练数据又用作测试数据，提高数据利用效率。

      K折交叉验证相对于验证集缺点：需要进行k次拆分、训练和评估，对于大型数据集来说计算消耗资源较大。

    2. LOOCV方法（留一交叉验证）：属于K=N的K折交叉验证，即在交叉验证的每次迭代中，仅使用数据集中的一条数据（一个样本）作为验证集，其余样本合并作为训练集。

      K折交叉验证相对于LOOCV优点：1. 只需要进行K次拆分、训练和评估，相对于LOOCV所使用的计算成本更低；2. 相比于LOOCV，K折交叉验证的验证集包含数据更多，能够更接近实际应用的表现，能够更准确的检测模型是否出现过拟合等现象。

      K折交叉验证相对于LOOCV缺点：由于K折交叉验证的每个验证集包含的数据更多，所以在性能评估中可能会导致更高的方差。

5.4.4

  • 使用自助法（Bootstrap）

    1. 生成自助样本：从原始数据集中有放回的抽取样本，生成B个自助样本（每个自助样本大小与原始数据集相同）。

      假设原始数据集为D = \{(X_1, Y_1), (X_2, Y_2), \dots, (X_n, Y_n)\}。

      那么B个自助样本为D^{(1)}, D^{(2)}, \dots, D^{(B)}。（每个样本大小为n）

    2. 将每一个自助样本D^{(b)}作为训练集拟合模型M^{(b)}。

    3. 使用每一个拟合好的模型，对新的预测点（题目中给出的特定值）X_0进行预测，得到B个预测响应变量\hat{Y}_0^{(1)}, \hat{Y}_0^{(2)}, \dots, \hat{Y}_0^{(B)}，并计算这B个响应变量的均值\bar{\hat{Y}}_0。

    4. 计算标准误差 \text{SE}(\hat{Y}_0) = \sqrt{\frac{1}{B-1} \sum_{b=1}^{B} \left( \hat{Y}_0^{(b)} - \bar{\hat{Y}}_0 \right)^2}。

  • 使用K折交叉验证法

    1. 将原始数据集D划分为K个大小尽可能相同的子集D_1, D_2, \dots, D_K。

    2. 对于每个子集D_i，将其作为验证集，其余子集合并作为训练集并拟合模型M^{(i)}。

    3. 使用每一个拟合好的模型，对新的预测点（题目中给出的特定值）X_0进行预测，得到K个预测响应变量\hat{Y}_0^{(1)}, \hat{Y}_0^{(2)}, \dots, \hat{Y}_0^{(K)}，并计算这K个响应变量的均值\bar{\hat{Y}}_0。

    4. 计算标准误差\text{SE}(\hat{Y}_0) = \sqrt{\frac{1}{K-1} \sum_{k=1}^{K} \left( \hat{Y}_0^{(k)} - \bar{\hat{Y}}_0 \right)^2}。

6.8.1

  • 最优子集选择：对于每个可能的模型大小k（模型中包含k个预测变量），计算当前大小下所有可能的组合并选择训练集RSS最小的模型作为当前大小的最优子集。

  • 向前逐步选择：从空模型开始，每一步加入一个预测变量，使加入后模型的训练RSS最小，直到模型大小达到p。

  • 向后逐步选择：从包含所有预测变量的模型（模型大小为p）开始，每一步删去一个预测变量，使删去后模型的训练RSS最小，直到最后得到空模型。

  • (a)

    最优子集选择的训练集RSS最小。因为最优子集选择是在当前模型大小下的所有可能组合中选择出对应训练RSS最小的模型。而其他两种方法每次只能增加或减少一个变量，可能会错过在限制模型大小为k的情况下的全局最优组合。

  • (b)

    无法确定三个模型哪个测试集RSS最小。因为三个模型都是在特定条件下找训练集RSS最小的情况，所以只能分析其在训练集上的表现，而测试集的表现要根据数据的情况来看。相对于最优子集选择，其他两种方法更倾向于选择简洁且泛化的模型，可能测试集表现更好；但是最优子集选择在选择中考虑的可能组合更多，也可能测试集表现更好。

  • (c)

    1. 对。向前逐步选择方法在求取(k+1)变量模型时，就是从已经得到的k变量模型尝试加入一个新变量，使得加入后的模型训练RSS最小。所以k变量模型中的预测变量集合一定是(k+1)变量模型预测变量集合的子集。

    2. 对。向前逐步选择方法在求取k变量模型时，就是从已经得到的(k+1)变量模型尝试删去一个变量，使得删去后的模型训练RSS最小。所以k变量模型中的预测变量集合一定是(k+1)变量模型预测变量集合的子集。

    3. 错。向前逐步选择从空模型开始，而向后逐步选择从包含所有预测变量的模型开始。二者在选择时的选择路径可能不同，所以不能说向后的k变量模型时向前的(k+1)变量模型的子集。

    4. 错。理由同上。

    5. 错。最优子集选择法所选择的k变量模型在所有模型大小为k的模型中选择RSS最小的，而(k+1)变量模型也是在所有模型大小为(k+1)的模型中选择RSS最小的。二者所包含的变量之间没有必然联系，也不能确定是否存在包含关系。

二、应用题

5.4.6

  • (a)

    # 6.(a)
library(ISLR)
glm.fit = glm(default~income+balance, data=Default, family=binomial)
summary(glm.fit)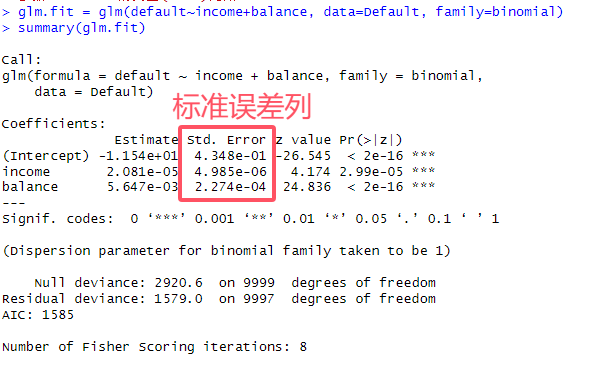

    image-20241021111649078

  • (b)

    # 6.(b)
boot.fn = function(data, index) {
  glm.fit = glm(default~income+balance, data=data, family=binomial, subset=index)
  return (coef(glm.fit)) # coef函数用于提取回归系数
}
boot.fn(Default, 1:nrow(Default)) # 使用整个数据集验证函数

    image-20241021113228680

  • (c)

    # 6.(d)
library(boot) # boot函数即是从给定数据集有放回抽样，得到n个与原数据集大小相等的数据集并应用function函数
boot(Default, boot.fn, 100)# 从Default数据集中进行引导抽样100次，每次调用 boot.fn 函数进行统计计算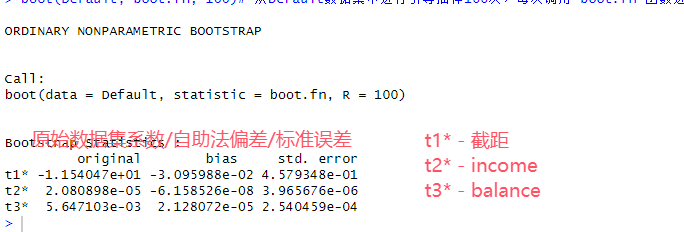

    image-20241021114150860

  • (d)

    # 6.(e)
##  std.E   income   balance
## 自助法 3.966e-06 2.540e-04
##  glm   4.985e-06 2.275e-04
## 二者得到的标准误差基本相等。
## 自助法更适用于复杂或非标准、样本较小的情况
## glm更适用于大样本和正泰误差分布的情况

  • 完整代码

    # 6.(a)
library(ISLR)
glm.fit = glm(default~income+balance, data=Default, family=binomial)
summary(glm.fit)
​
# 6.(b)
boot.fn = function(data, index) {
  glm.fit = glm(default~income+balance, data=data, family=binomial, subset=index)
  return (coef(glm.fit)) # coef函数用于提取回归系数
}
boot.fn(Default, Default) # 使用整个数据集验证函数
​
# 6.(d)
library(boot) # boot函数即是从给定数据集有放回抽样，得到n个与原数据集大小相等的数据集并应用function函数
boot(Default, boot.fn, 100)# 从Default数据集中进行引导抽样100次，每次调用 boot.fn 函数进行统计计算
​
# 6.(e)
##  std.E   income   balance
## 自助法 3.966e-06 2.540e-04
##  glm   4.985e-06 2.275e-04
## 二者得到的标准误差基本相等。
## 自助法更适用于复杂或非标准、样本较小的情况
## glm更适用于大样本和正泰误差分布的情况

5.4.8

  • (a)

    # 8.(a)
set.seed(1)
y=rnorm(100) # 生成100个符合标准正态分布的随机变量
x=rnorm(100)
y=x-2*x^2+rnorm(100)
## n：样本数量100
## p：自变量数量1
## 模型：y=x-2x²+ε

    image-20241021150117966

  • (b)

    # 8.(b)
plot(x, y, main="y=x-2x²+ε")
## 根据x、y的散点图可以看出二者具有二次关系，与模型方程表述基本相同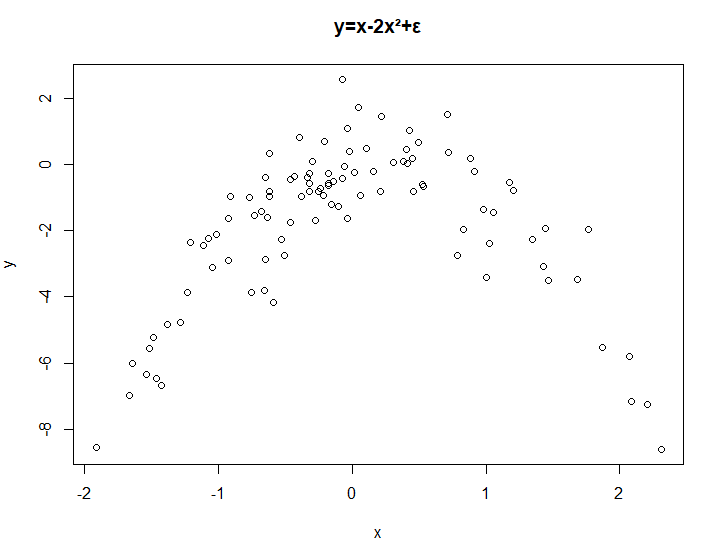

    image-20241021150508625

  • (c)

    # 8.(c)
library(boot)
set.seed(1)
data = data.frame(x, y)
## Y=β0+β1X+ε
model1 = glm(y~x, data=data)
loocv.error1 = cv.glm(data, model1)$delta[1]
### cv.glm函数得到的：
### 1.delta[1] 估计的交叉验证误差 ## 2.delta[2] 带有偏差校正的交叉验证误差
### 3. call 函数调用列表 ## 4. K 表示如果为k折交叉验证时的折叠数量，LOOCV中为n
## Y=β0+β1X+β2X^2+ε
model2 = glm(y~x+I(x^2), data=data)
loocv.error2 = cv.glm(data, model2)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+ε
model3 = glm(y~x+I(x^2)+I(x^3), data=data)
loocv.error3 = cv.glm(data, model3)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+β4X^4+ε
model4 = glm(y~x+I(x^2)+I(x^3)+I(x^4), data=data)
loocv.error4 = cv.glm(data, model4)$delta[1]
loocv_errors = c(loocv.error1, loocv.error2, loocv.error3, loocv.error4) # c用于将多个值组合为一个向量
names(loocv_errors) = c("Model1", "Model2", "Model3", "Model4")
print(loocv_errors)
### 根据结果model2的loocv误差最小，也验证了二者之间最接近二次关系

    image-20241021152141938

  • (d)

    # 8.(d)
set.seed(100)
## Y=β0+β1X+ε
model1 = glm(y~x, data=data)
loocv.error1 = cv.glm(data, model1)$delta[1]
## Y=β0+β1X+β2X^2+ε
model2 = glm(y~x+I(x^2), data=data)
loocv.error2 = cv.glm(data, model2)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+ε
model3 = glm(y~x+I(x^2)+I(x^3), data=data)
loocv.error3 = cv.glm(data, model3)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+β4X^4+ε
model4 = glm(y~x+I(x^2)+I(x^3)+I(x^4), data=data)
loocv.error4 = cv.glm(data, model4)$delta[1]
loocv_errors = c(loocv.error1, loocv.error2, loocv.error3, loocv.error4) # c用于将多个值组合为一个向量
names(loocv_errors) = c("Model1", "Model2", "Model3", "Model4")
print(loocv_errors)
### 结果没有任何变化
### 因为LOOCV中会不重复的每次拿一条数据作为验证集其余作为训练集，不存在随机性
### 所以改变随机种子对该方法的结果没有影响

    image-20241021152610437

  • (e)

    # 8.(e)
## 可以发现模型2（即二次模型）效果最好，因为在设置x和y的值的时候利用的二次函数
## 那么x和y的真实情况也是最符合二次条件的
## 二次模型更贴近x和y的真实情况，那么LOOCV验证得到的误差也是最小的。

  • (f)

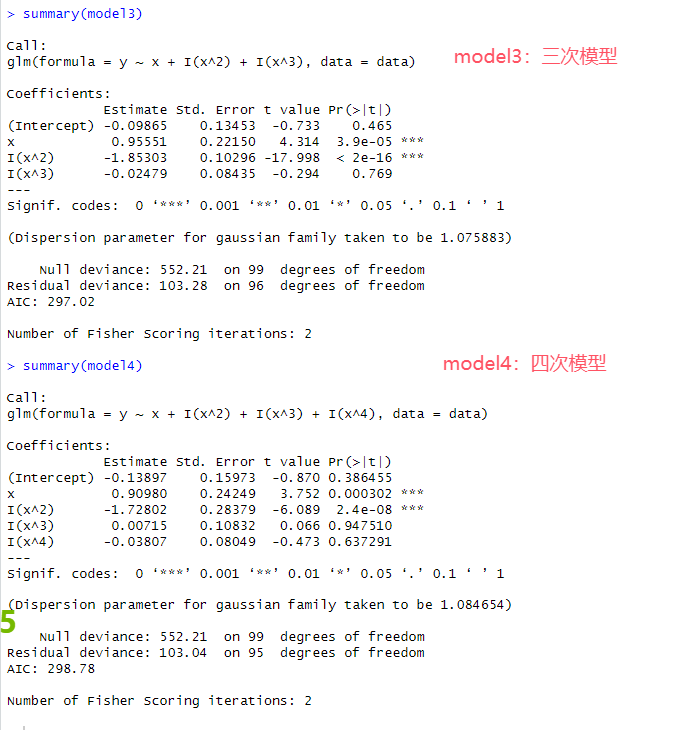
    # 8.(f)
summary(model1)
summary(model2)
summary(model3)
summary(model4)
## 首先发现在Model1中，x的p值小，具有显著关系；在其他三个模型中，x和x^2都具有显著关系，与真实情况相符
## 四个模型中，Model2的Residual deviance（残差偏差）比较小，说明拟合效果比较好
## 四个模型中，Model2的AIC最小，表示模型在平衡拟合度和复杂度最好，也最接近真实情况
## 在LOOCV验证中得到Model2拟合效果最好，在四个模型中也是Model2最接近真实情况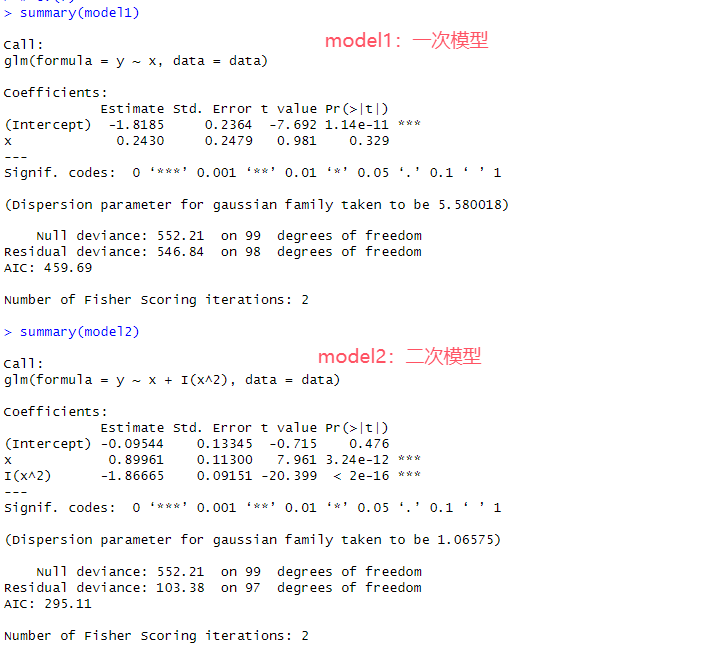

    image-20241021153055044

    image-20241021153123948

  • 完整代码

    # 8.(a)
set.seed(1)
y=rnorm(100) # 生成100个符合标准正态分布的随机变量
x=rnorm(100)
y=x-2*x^2+rnorm(100)
## n：样本数量100
## p：自变量数量1
## 模型：y=x-2x²+ε
​
# 8.(b)
plot(x, y, main="y=x-2x²+ε")
## 根据x、y的散点图可以看出二者具有二次关系，与模型方程表述基本相同
​
# 8.(c)
library(boot)
set.seed(1)
data = data.frame(x, y)
## Y=β0+β1X+ε
model1 = glm(y~x, data=data)
loocv.error1 = cv.glm(data, model1)$delta[1]
### cv.glm函数得到的：
### 1.delta[1] 估计的交叉验证误差 ## 2.delta[2] 带有偏差校正的交叉验证误差
### 3. call 函数调用列表 ## 4. K 表示如果为k折交叉验证时的折叠数量，LOOCV中为n
## Y=β0+β1X+β2X^2+ε
model2 = glm(y~x+I(x^2), data=data)
loocv.error2 = cv.glm(data, model2)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+ε
model3 = glm(y~x+I(x^2)+I(x^3), data=data)
loocv.error3 = cv.glm(data, model3)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+β4X^4+ε
model4 = glm(y~x+I(x^2)+I(x^3)+I(x^4), data=data)
loocv.error4 = cv.glm(data, model4)$delta[1]
loocv_errors = c(loocv.error1, loocv.error2, loocv.error3, loocv.error4) # c用于将多个值组合为一个向量
names(loocv_errors) = c("Model1", "Model2", "Model3", "Model4")
print(loocv_errors)
### 根据结果model2的loocv误差最小，也验证了二者之间最接近二次关系
​
# 8.(d)
set.seed(100)
## Y=β0+β1X+ε
model1 = glm(y~x, data=data)
loocv.error1 = cv.glm(data, model1)$delta[1]
## Y=β0+β1X+β2X^2+ε
model2 = glm(y~x+I(x^2), data=data)
loocv.error2 = cv.glm(data, model2)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+ε
model3 = glm(y~x+I(x^2)+I(x^3), data=data)
loocv.error3 = cv.glm(data, model3)$delta[1]
## Y=β0+β1X+β2X^2+β3X^3+β4X^4+ε
model4 = glm(y~x+I(x^2)+I(x^3)+I(x^4), data=data)
loocv.error4 = cv.glm(data, model4)$delta[1]
loocv_errors = c(loocv.error1, loocv.error2, loocv.error3, loocv.error4) # c用于将多个值组合为一个向量
names(loocv_errors) = c("Model1", "Model2", "Model3", "Model4")
print(loocv_errors)
### 结果没有任何变化
### 因为LOOCV中会不重复的每次拿一条数据作为验证集其余作为训练集，不存在随机性
### 所以改变随机种子对该方法的结果没有影响
​
# 8.(e)
## 可以发现模型2（即二次模型）效果最好，因为在设置x和y的值的时候利用的二次函数
## 那么x和y的真实情况也是最符合二次条件的
## 二次模型更贴近x和y的真实情况，那么LOOCV验证得到的误差也是最小的。
​
# 8.(f)
summary(model1)
summary(model2)
summary(model3)
summary(model4)
## 首先发现在Model1中，x的p值小，具有显著关系；在其他三个模型中，x和x^2都具有显著关系，与真实情况相符
## 四个模型中，Model2的Residual deviance（残差偏差）比较小，说明拟合效果比较好
## 四个模型中，Model2的AIC最小，表示模型在平衡拟合度和复杂度最好，也最接近真实情况
## 在LOOCV验证中得到Model2拟合效果最好，在四个模型中也是Model2最接近真实情况

5.4.9

  • (a)

    # 9.(a)
library(MASS)
attach(Boston)
mu_hat = mean(medv) # μ^=medv的均值
mu_hat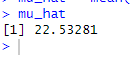

    image-20241021154509285

  • (b)

    # 9.(b)
n = length(medv)
mu_hat.se = sd(medv)/sqrt(n) # 样本均值SE=SD/sqrt(n)
mu_hat.se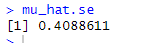

    image-20241021154811433

  • (c)

    # 9.(c)
library(boot)
boot_fn_mean = function(data, index) { # 计算均值的函数（引导函数）
  result = mean(data[index])
  return (result)
}
set.seed(1)
boot.mean = boot(medv, boot_fn_mean, 2000) # 通过对medv随机抽样执行b_f_m函数，共2000次
boot.mean
## 自助法se为0.4052 之前的SE为0.4089
## 二者几乎相等，说明了标准误差基本为这个值并且原数据基本符合正态分布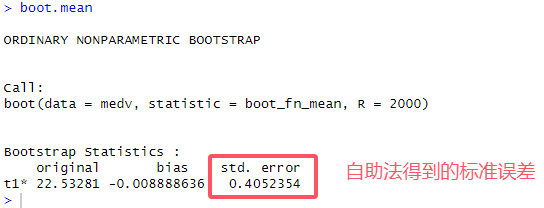

    image-20241021155634451

  • (d)

    # 9.(d)
boot.mean = boot.result$t0 ## 得到自助法μ^
boot.se = sd(boot.result$t) ## 得到自助法SE
boot.ci = c(boot.mean-2*boot.se, boot.mean+2*boot.se)
t.ci = t.test(medv)
print(boot.ci)
print(t.ci)
## 二者置信区间几乎相同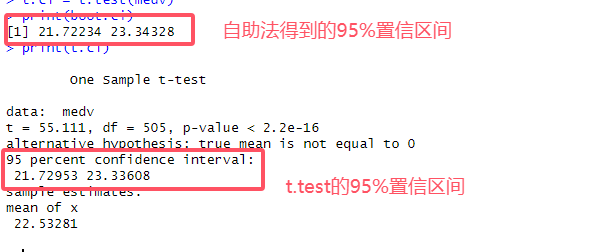

    image-20241021160752248

  • (e)

    # 9.(e)
mu_hat_med = median(medv)
mu_hat_med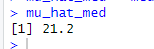

    image-20241021161001271

  • (f)

    # 9.(f)
boot_fn_med = function(data, index) {
  result = median(data[index])
  return (result)
}
boot.result = boot(medv, boot_fn_med, 2000)
boot.result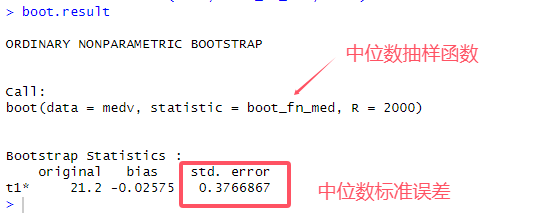

    image-20241021161241121

  • (g)

    # 9.(g)
mu_hat_10_div = quantile(medv, 0.1) # quantile计算指定概率的分位数
mu_hat_10_div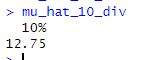

    image-20241021161533013

  • (h)

    # 9.(h)
boot_fn_10_div = function(data, index) {
  result = quantile(data[index], 0.1)
  return (result)
}
boot.result = boot(medv, boot_fn_10_div, 2000)
boot.result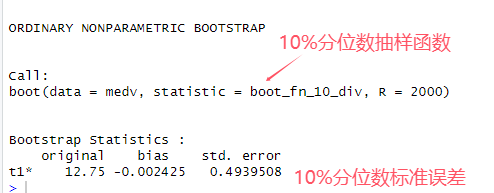

    image-20241021161900539

  • 完整代码

    # 9.(a)
library(MASS)
attach(Boston)
mu_hat = mean(medv) # μ^=medv的均值
mu_hat
​
# 9.(b)
n = length(medv)
mu_hat.se = sd(medv)/sqrt(n) # 样本均值SE=SD/sqrt(n)
mu_hat.se
​
# 9.(c)
library(boot)
boot_fn_mean = function(data, index) { # 计算均值的函数（引导函数）
  result = mean(data[index])
  return (result)
}
set.seed(1)
boot.result = boot(medv, boot_fn_mean, 2000) # 通过对medv随机抽样执行b_f_m函数，共2000次
boot.result
## 自助法se为0.4052 之前的SE为0.4089
## 二者几乎相等，说明了标准误差基本为这个值并且原数据基本符合正态分布
​
# 9.(d)
boot.mean = boot.result$t0 ## 得到自助法μ^
boot.se = sd(boot.result$t) ## 得到自助法SE
boot.ci = c(boot.mean-2*boot.se, boot.mean+2*boot.se)
t.ci = t.test(medv)
print(boot.ci)
print(t.ci)
## 二者置信区间几乎相同
​
# 9.(e)
mu_hat_med = median(medv)
mu_hat_med
​
# 9.(f)
boot_fn_med = function(data, index) {
  result = median(data[index])
  return (result)
}
boot.result = boot(medv, boot_fn_med, 2000)
boot.result
​
# 9.(g)
mu_hat_10_div = quantile(medv, 0.1) # quantile计算指定概率的分位数
mu_hat_10_div
​
# 9.(h)
boot_fn_10_div = function(data, index) {
  result = quantile(data[index], 0.1)
  return (result)
}
boot.result = boot(medv, boot_fn_10_div, 2000)
boot.result