本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为8.4节、9.7节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

8.4.2

image-20241106214645828

8.4.3

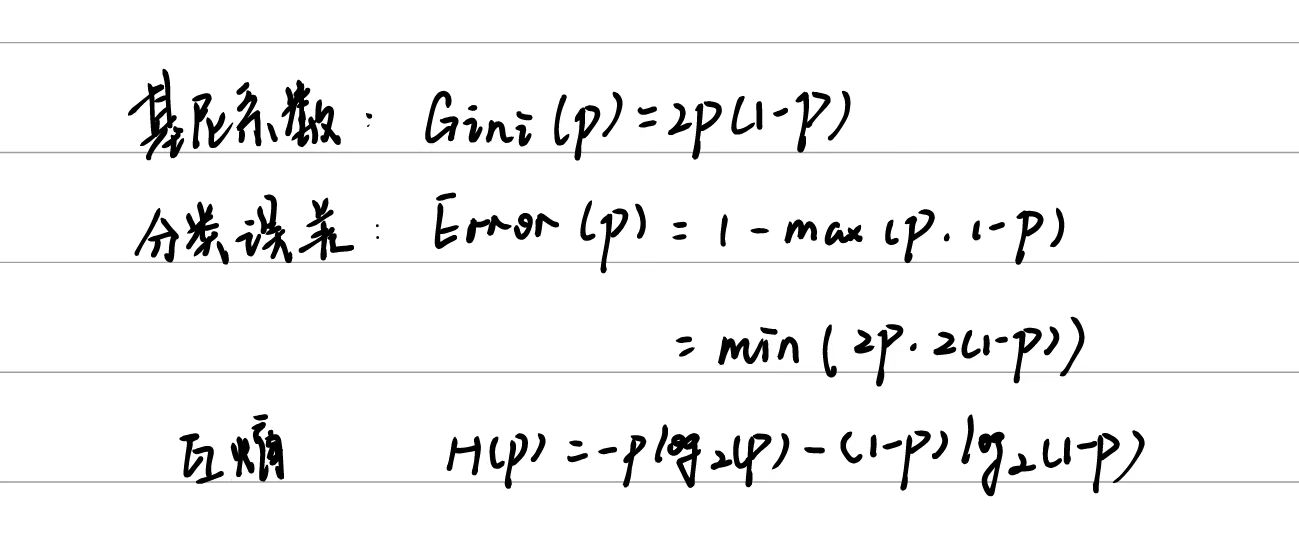
image-20241106215022059

# 定义概率范围
p = seq(0, 1, by = 0.01)
# 计算基尼系数
gini = 2 * p * (1 - p)
#gini = 1 - p^2 - (1-p)^2
# 计算分类误差
error = pmin(2 * p, 2 * (1 - p))
# 计算互熵
mutual_info = -p * log2(p) - (1 - p) * log2(1 - p)
# 绘图
plot(p, gini, type = "l", col = "red", xlab = "p", ylab = "Value", ylim = c(0, 1), main = "Gini, Error, and Mutual Information")
lines(p, error, type = "l", col = "blue")
lines(p, mutual_info, type = "l", col = "green")
legend("topright", legend = c("Gini", "Error", "Mutual Information"), col = c("red", "blue", "green"), lty = 1)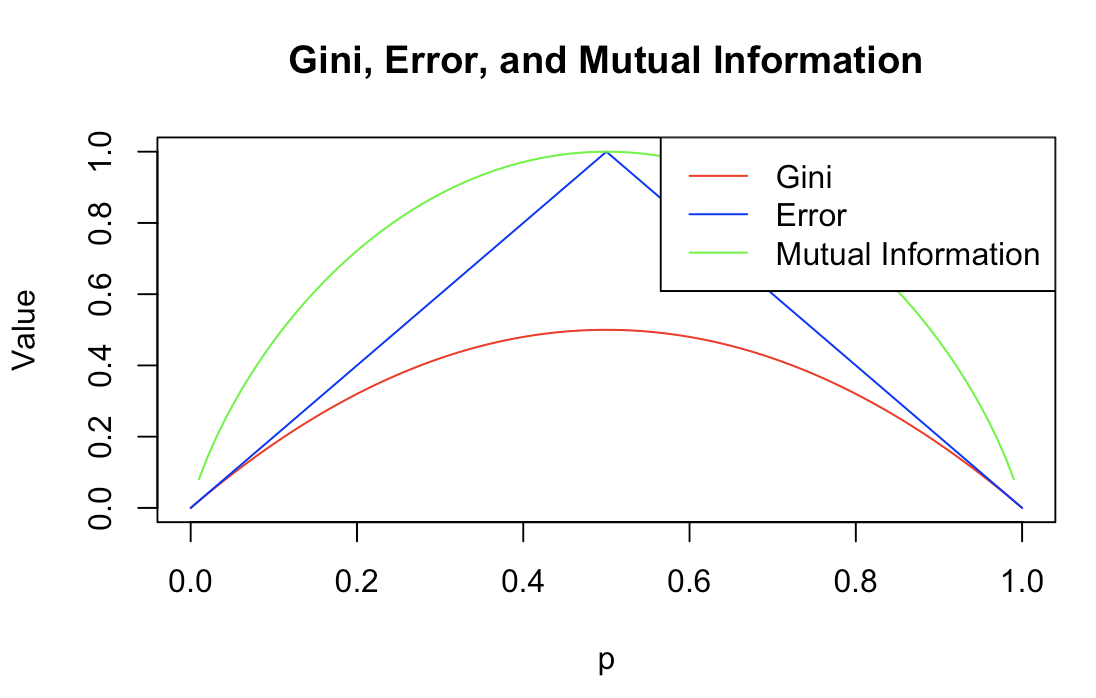

image-20241106215654460

8.4.5

  • 多数投票：当P(类别是Red|X的概率)大于0.5的时候，认为数据是Red类别。而满足P>0.5的数据有6个，也就是这6个数据指向Red类，剩下4个数据指向Green类，所以根据多数投票，该数据为Red。

  • 平均概率：该数据为Red的平均概率为0.45，小于0.5，故认为Green。

9.7.2

  • (a)

    # 设置图形窗口
plot(-3:1, 0:4, type = "n", xlab = expression(X[1]), ylab = expression(X[2]), asp = 1)
title(main = expression((1 + X[1])^2 + (2 - X[2])^2 == 4))
# 计算圆的坐标
theta <- seq(0, 2 * pi, length.out = 200)
x <- -1 + 2 * cos(theta)
y <- 2 + 2 * sin(theta)
# 绘制圆
lines(x, y, col = "blue", lwd = 2)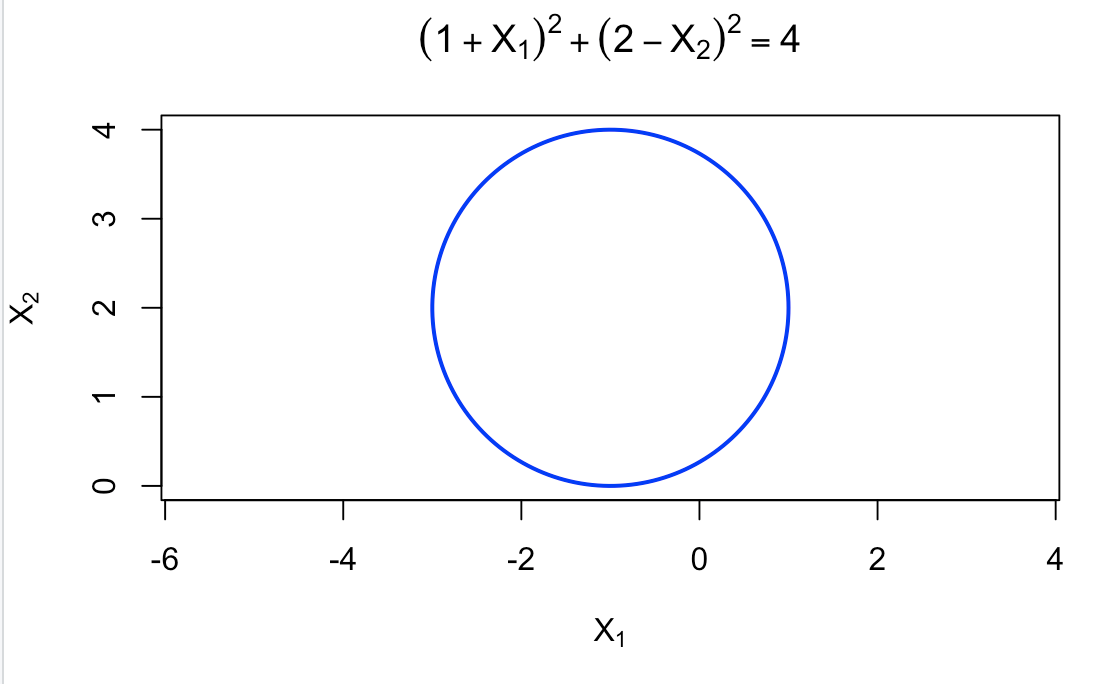

    image-20241106221645792

  • (b)

    # 填充圆外部（>4的点集）
rect(par("usr")[1], par("usr")[3], par("usr")[2], par("usr")[4], col = "grey")
polygon(x, y, col = "white", border = NA)
# 填充圆内部（<=4的点集）
polygon(x, y, col = "white", border = NA)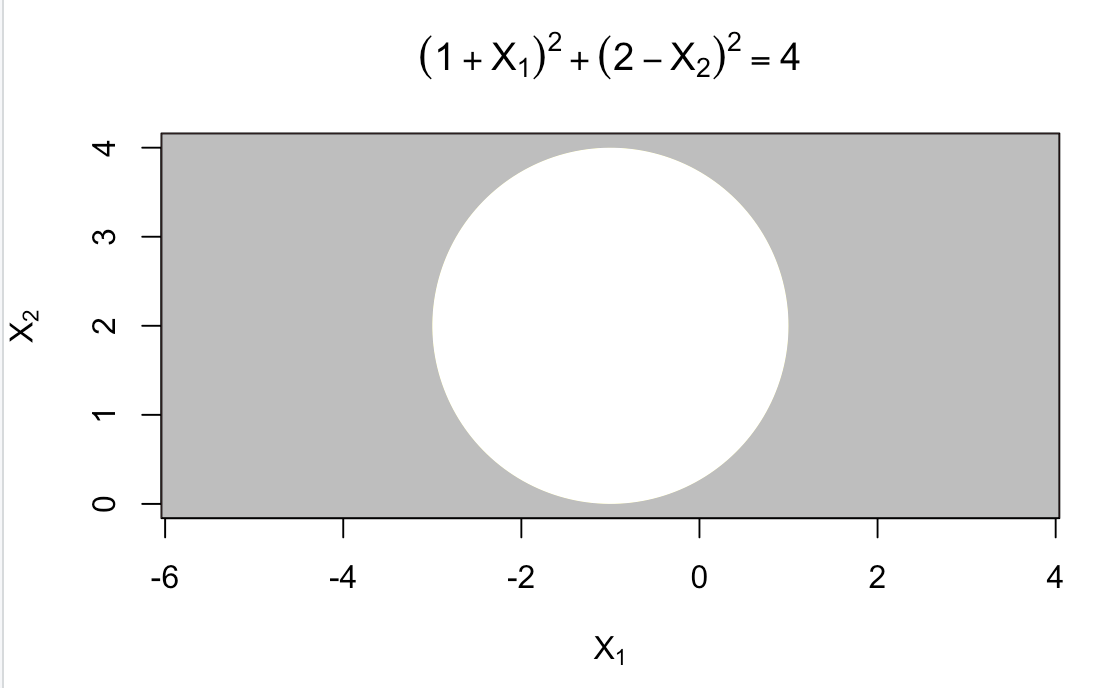

    image-20241106221935118

    灰色为>4点集，白色为<4点集。

  • (c)

    (0,0):蓝色 (-1,1):红色 (2,2):蓝色 (3,8):蓝色

  • (d)

    化简后可以得到5+2X_1-4X_2+X_1^2+X_2^2\gt4。

    这个决策边界对于X_1和X_2不是线性的，但是对于X_1,X_2,X_1^2,X_2^2是线性的。

9.7.3

  • (a)

    # 定义数据
x1 <- c(3, 2, 4, 1, 2, 4, 4)
x2 <- c(4, 2, 4, 4, 1, 3, 1)
# 定义颜色（根据类别）
colors <- c("red", "red", "red", "red", "blue", "blue", "blue")
# 绘制散点图
plot(x1, x2, col = colors, pch = 16, xlim = c(0, 5), ylim = c(0, 5), xlab = "X1", ylab = "X2", main = "Scatter Plot of X1 vs X2")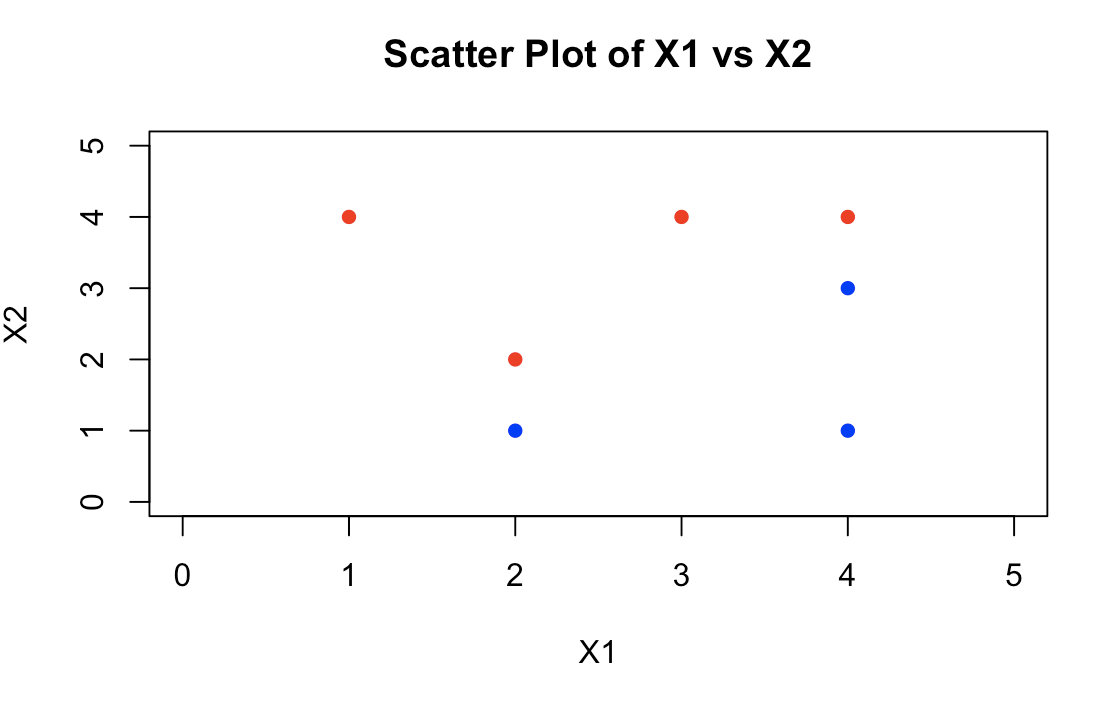
​

    image-20241106222538941

  • (b) 决策边界表达式：-X_1+X_2+0.5\gt0。

  • (c)

    \beta_0=0.5,\beta_1=-1,\beta_2=1。

  • (d)

    plot(x1, x2, col = colors, xlim = c(0, 5), ylim = c(0, 5))
abline(-0.5, 1)
abline(-1, 1, lty = 2)
abline(0, 1, lty = 2)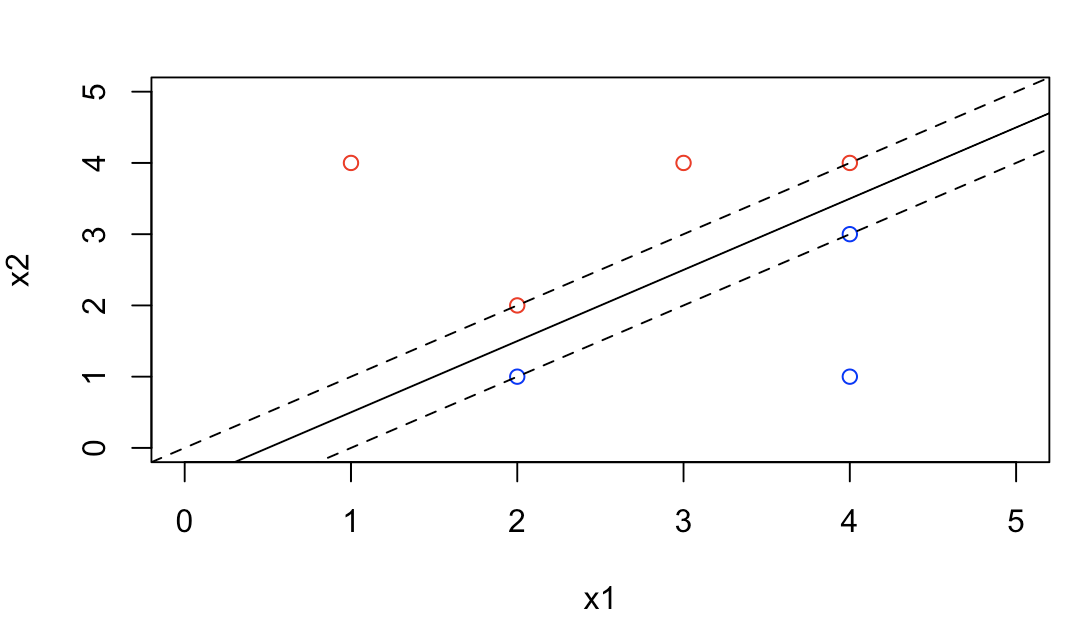

    image-20241106223035872

  • (e)

    支持向量为坐标(2,1) (4,3) (2,2) (4,4)的四个数据。

  • (f)

    非支持向量的移动对于决策边界的影响较小，而且第七个观测点距离间隔较远，它的轻微移动并不会影响最大间隔超平面。

  • (g)

    表达式：-X_1+X_2+0.8=0。

  • (h)

    plot(x1, x2, col = colors, xlim = c(0, 5), ylim = c(0, 5))
points(c(4), c(2), col = c("red"))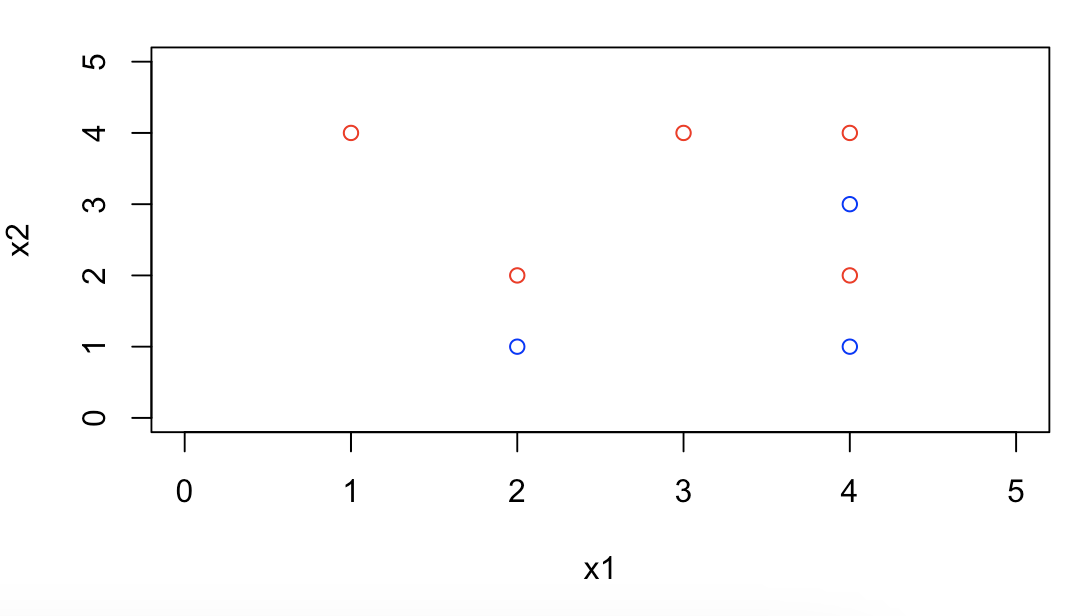

    image-20241106223305369

二、应用题

8.4.8

  • (a)

    # 8.(a)
library(ISLR)
attach(Carseats)
set.seed(1)
train = sample(dim(Carseats)[1], dim(Carseats)[1]/2)
Carseats.train = Carseats[train, ]
Carseats.test = Carseats[-train, ]

    image-20241106223516466

  • (b)

    # 8.(b)
library(tree)
tree.carseats = tree(Sales ~ ., data = Carseats.train)
summary(tree.carseats)
plot(tree.carseats)
text(tree.carseats, pretty = 0)
pred.carseats = predict(tree.carseats, Carseats.test)
mean((Carseats.test$Sales - pred.carseats)^2)
## 可以看出较为重要的变量为 Price，得到的测试错误率为 4.922039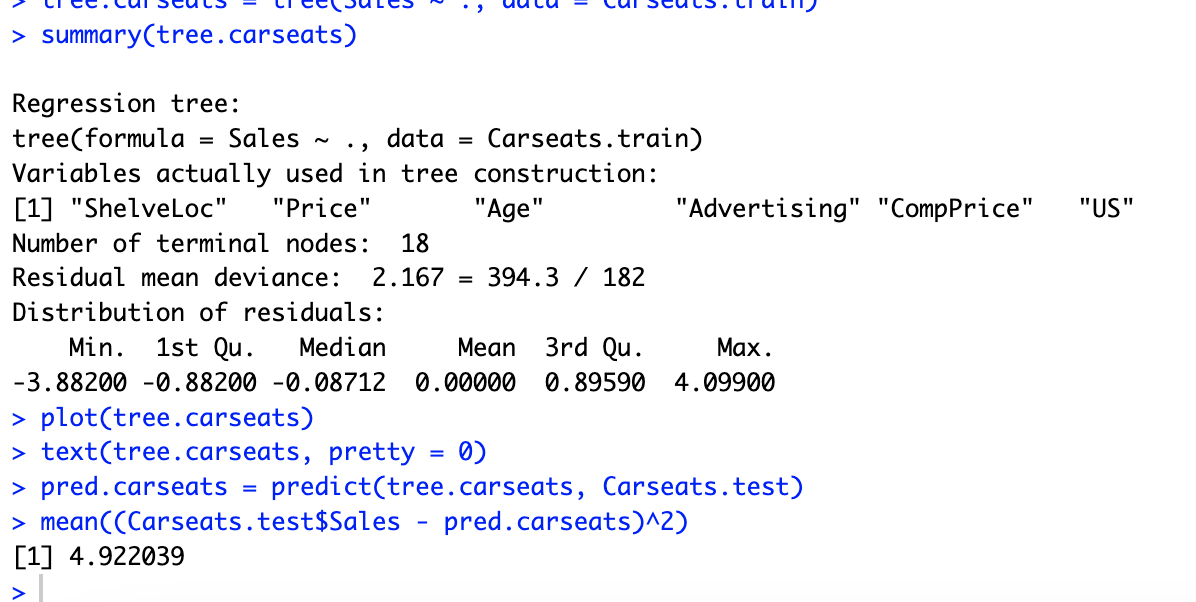

    image-20241106223655325

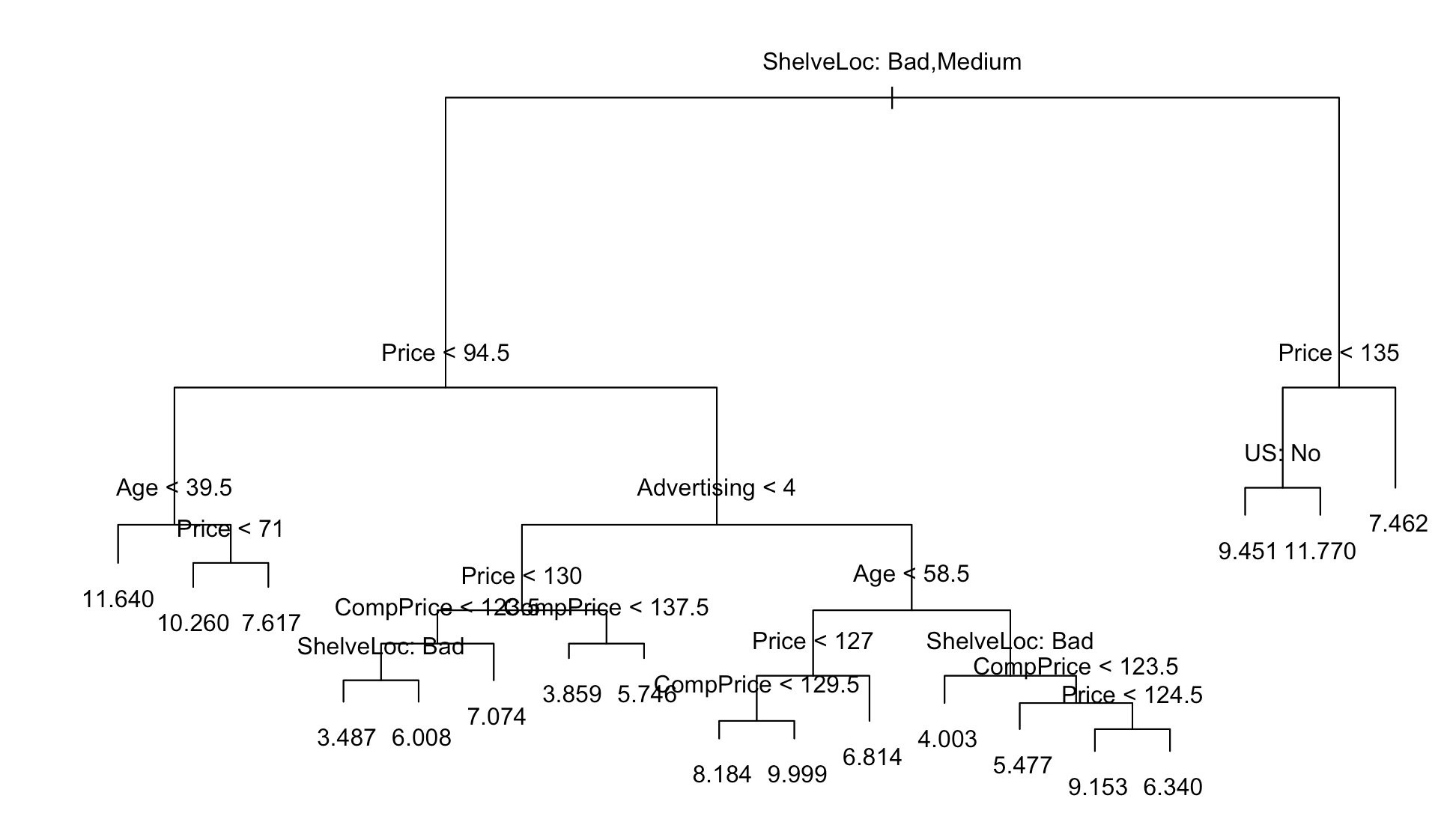
    image-20241106223628011

  • (c)

    # 8.(c)
cv.carseats = cv.tree(tree.carseats, FUN = prune.tree)
par(mfrow = c(1, 2))
plot(cv.carseats$size, cv.carseats$dev, type = "b")
plot(cv.carseats$k, cv.carseats$dev, type = "b")
## 可以观察得到剪枝后的回归树并不一定能够减小 MSE，相反，未剪枝的模型具有最小的 MSE。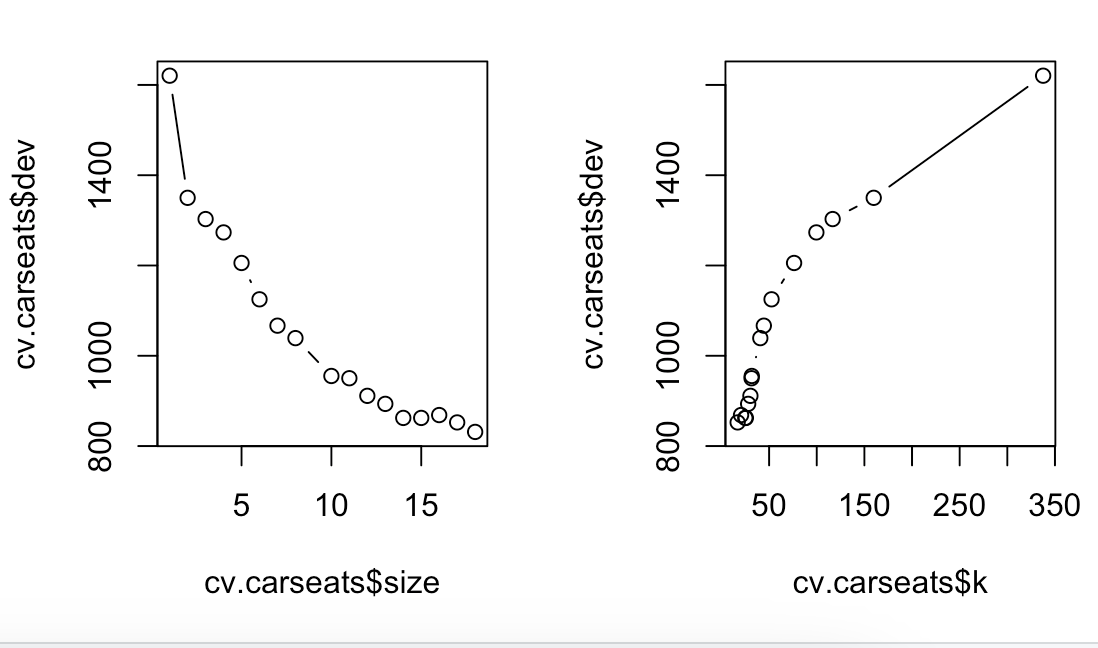

    image-20241106223842210

  • (d)

    # 8.(d)
library(randomForest)
bag.carseats = randomForest(Sales ~ ., data = Carseats.train, mtry =10, ntree = 500, importance = T)
bag.pred = predict(bag.carseats, Carseats.test)
mean((Carseats.test$Sales - bag.pred)^2)
importance(bag.carseats)
## 测试错误率为 2.622982。
## 可以看出： 较为重要的变量有 Price、 ShelveLoc、 CompPrice 和 Age 等等。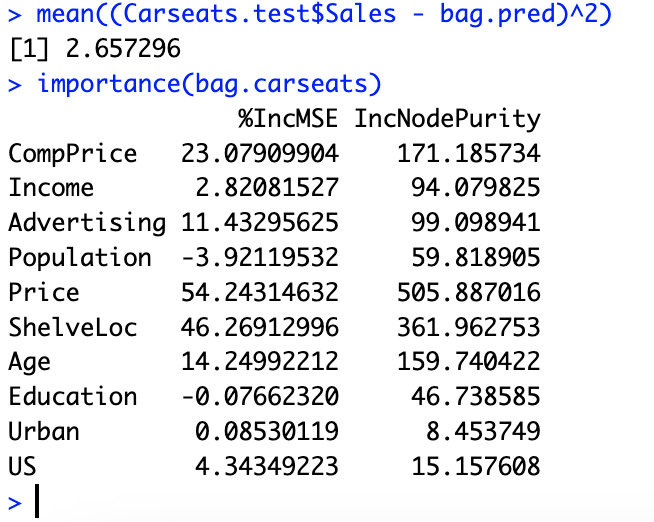

    image-20241106224129727

  • (e)

    # 8.(e)
rf.carseats = randomForest(Sales ~ ., data = Carseats.train, mtry = 5,ntree = 500,importance = T)
rf.pred = predict(rf.carseats, Carseats.test)
mean((Carseats.test$Sales - rf.pred)^2)
importance(rf.carseats)
## 测试错误率为 2.70217。
##较为重要的变量有 Price、ShelveLoc、CompPrice 和 Age 等等。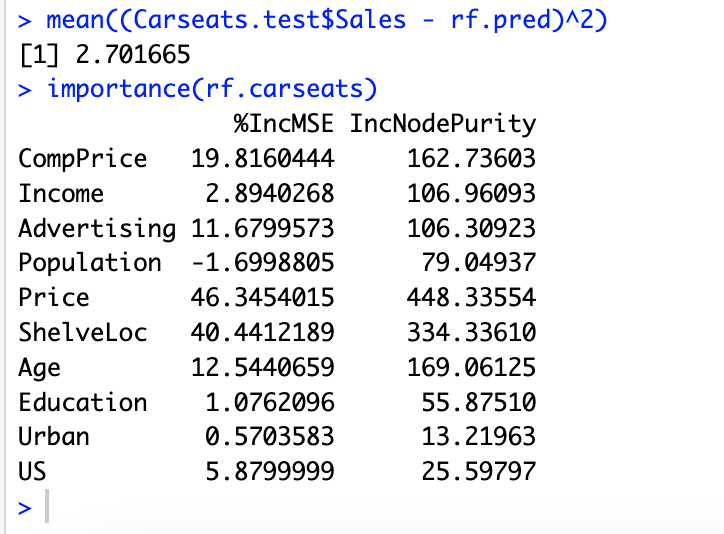

    image-20241106224252854

  • 完整代码

    # 8.(a)
library(ISLR)
attach(Carseats)
set.seed(1)
train = sample(dim(Carseats)[1], dim(Carseats)[1]/2)
Carseats.train = Carseats[train, ]
Carseats.test = Carseats[-train, ]
​
# 8.(b)
library(tree)
tree.carseats = tree(Sales ~ ., data = Carseats.train)
summary(tree.carseats)
plot(tree.carseats)
text(tree.carseats, pretty = 0)
pred.carseats = predict(tree.carseats, Carseats.test)
mean((Carseats.test$Sales - pred.carseats)^2)
## 可以看出较为重要的变量为 Price，得到的测试错误率为 4.922039
​
# 8.(c)
cv.carseats = cv.tree(tree.carseats, FUN = prune.tree)
par(mfrow = c(1, 2))
plot(cv.carseats$size, cv.carseats$dev, type = "b")
plot(cv.carseats$k, cv.carseats$dev, type = "b")
## 可以观察得到剪枝后的回归树并不一定能够减小 MSE，相反，未剪枝的模型具有最小的 MSE。
​
# 8.(d)
library(randomForest)
bag.carseats = randomForest(Sales ~ ., data = Carseats.train, mtry =10, ntree = 500, importance = T)
bag.pred = predict(bag.carseats, Carseats.test)
mean((Carseats.test$Sales - bag.pred)^2)
importance(bag.carseats)
## 测试错误率为 2.622982。
## 可以看出： 较为重要的变量有 Price、 ShelveLoc、 CompPrice 和 Age 等等。
​
# 8.(e)
rf.carseats = randomForest(Sales ~ ., data = Carseats.train, mtry = 5,ntree = 500,importance = T)
rf.pred = predict(rf.carseats, Carseats.test)
mean((Carseats.test$Sales - rf.pred)^2)
importance(rf.carseats)
## 测试错误率为 2.70217。
##较为重要的变量有 Price、ShelveLoc、CompPrice 和 Age 等等。

8.4.9

  • (a)

    # 9.(a)
library(ISLR)
attach(OJ)
set.seed(1013)
train = sample(dim(OJ)[1], 800)
OJ.train = OJ[train, ]
OJ.test = OJ[-train, ]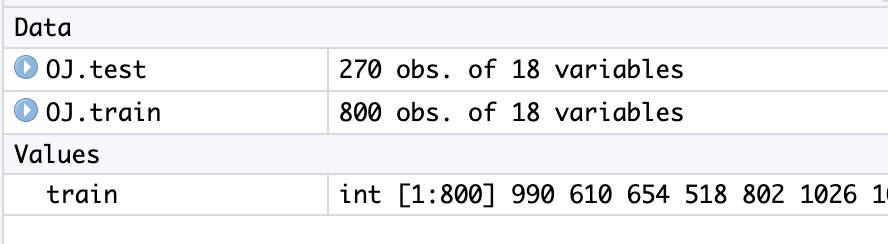

    image-20241106224435292

  • (b)

    # 9.(b)
library(tree)
oj.tree = tree(Purchase ~., data = OJ.train)
summary(oj.tree)

    image-20241106224535080

  • (c)

    # 9.(c)
oj.tree
## 以结点10作为分析：该结点以PriceDiff<0.065作为分割依据，其下共有75个数据
## 所有点的偏差为75.06。该结点上的预测是Sales=MM。 
## 该节点中约有20%的数据认为Sales=CH，剩下的80%数据认为Sales=MM。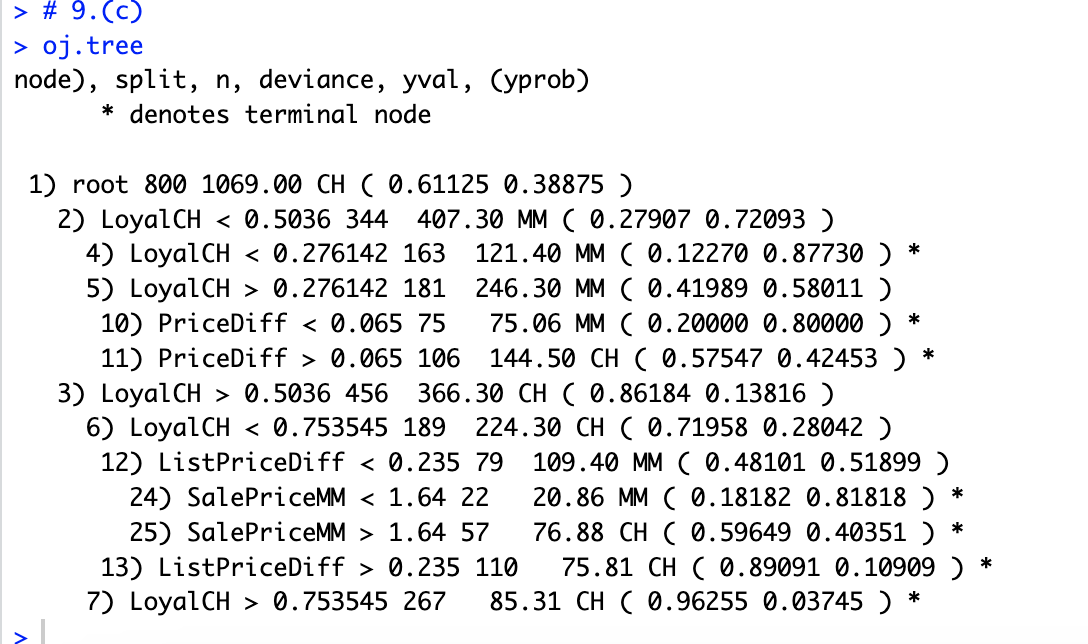

    image-20241106224611990

  • (d)

    # 9.(d)
par(mfrow=c(1,1))
plot(oj.tree)
text(oj.tree, pretty = 0)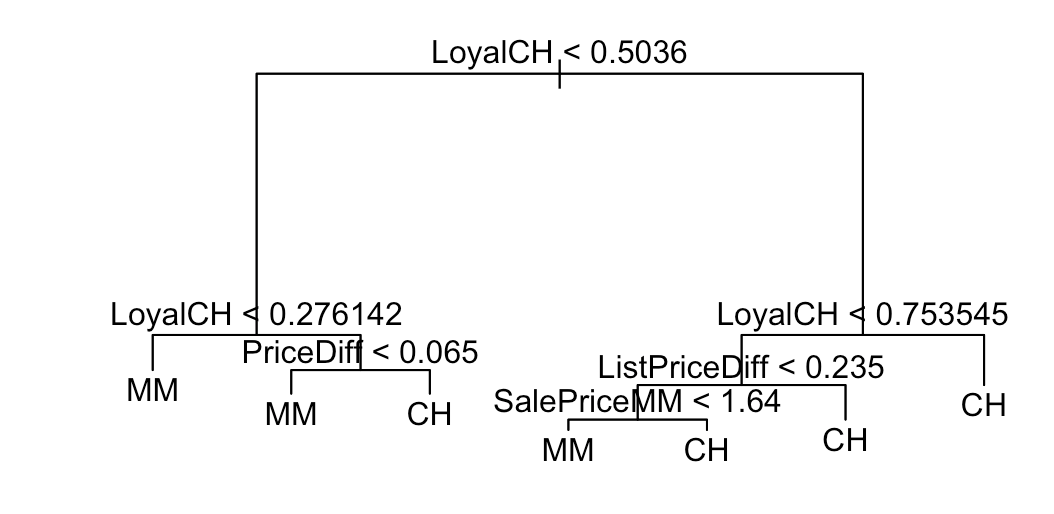

    image-20241106224811748

  • (e)

    # 9.(e)
oj.pred = predict(oj.tree, OJ.test, type = "class")
table(OJ.test$Purchase, oj.pred)
(15+30)/(149+15+30+76)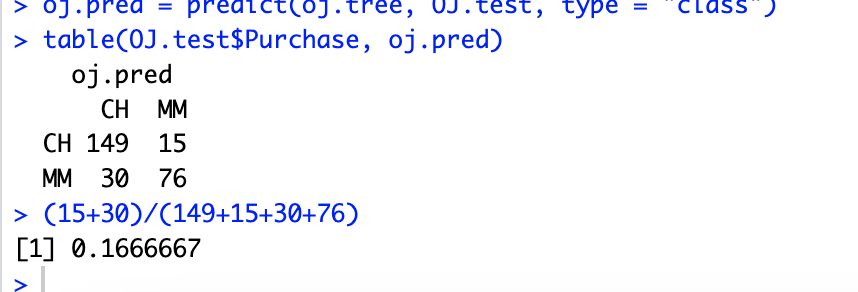

    image-20241106224913038

  • (f)

    # 9.(f)
cv.oj = cv.tree(oj.tree, FUN = prune.tree)

  • (g)

    # 9.(g)
plot(cv.oj$size, cv.oj$dev, type = "b", xlab = "Tree Size", ylab = "Deviance")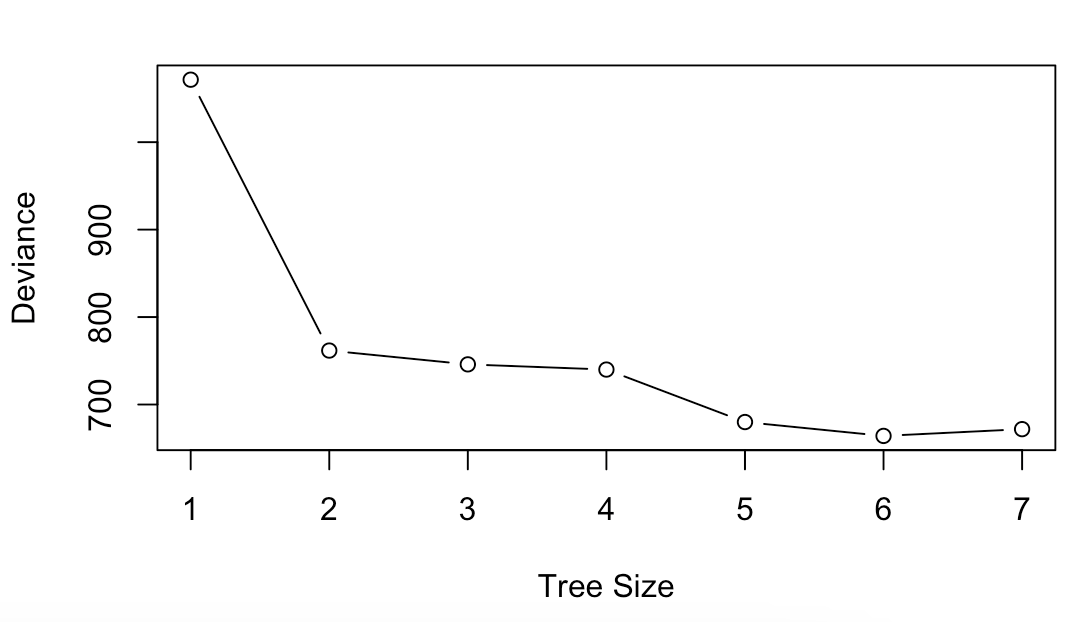

    image-20241106225041058

  • (h)

    # 9.(h)
## 可以看出：当 Size=6 的时候，利用交叉验证分类错误率最低

  • (i)

    # 9.(i)
oj.pruned = prune.tree(oj.tree, best = 6)

  • (j)

    # 9.(j)
summary(oj.pruned)

    image-20241106225312212

  • (k)

    # 9.(k)
pred.unpruned = predict(oj.tree, OJ.test, type = "class") 
misclass.unpruned = sum(OJ.test$Purchase != pred.unpruned)
misclass.unpruned/length(pred.unpruned)
pred.pruned = predict(oj.pruned, OJ.test, type = "class")
misclass.pruned = sum(OJ.test$Purchase != pred.pruned)
misclass.pruned/length(pred.pruned)
## 剪枝前后的测试错误率分别为 0.1666667 和 0.2， 因此剪枝之后的测试错误率更高

    image-20241106225422106

  • 完整代码

    # 9.(a)
library(ISLR)
attach(OJ)
set.seed(1013)
train = sample(dim(OJ)[1], 800)
OJ.train = OJ[train, ]
OJ.test = OJ[-train, ]
​
# 9.(b)
library(tree)
oj.tree = tree(Purchase ~., data = OJ.train)
summary(oj.tree)
​
# 9.(c)
oj.tree
## 以结点10作为分析：该结点以PriceDiff<0.065作为分割依据，其下共有75个数据
## 所有点的偏差为75.06。该结点上的预测是Sales=MM。 
## 该节点中约有20%的数据认为Sales=CH，剩下的80%数据认为Sales=MM。
​
# 9.(d)
par(mfrow=c(1,1))
plot(oj.tree)
text(oj.tree, pretty = 0)
​
# 9.(e)
oj.pred = predict(oj.tree, OJ.test, type = "class")
table(OJ.test$Purchase, oj.pred)
(15+30)/(149+15+30+76)
​
# 9.(f)
cv.oj = cv.tree(oj.tree, FUN = prune.tree)
​
# 9.(g)
plot(cv.oj$size, cv.oj$dev, type = "b", xlab = "Tree Size", ylab = "Deviance")
​
# 9.(h)
## 可以看出：当 Size=6 的时候，利用交叉验证分类错误率最低
​
# 9.(i)
oj.pruned = prune.tree(oj.tree, best = 6)
​
# 9.(j)
summary(oj.pruned)
​
# 9.(k)
pred.unpruned = predict(oj.tree, OJ.test, type = "class") 
misclass.unpruned = sum(OJ.test$Purchase != pred.unpruned)
misclass.unpruned/length(pred.unpruned)
pred.pruned = predict(oj.pruned, OJ.test, type = "class")
misclass.pruned = sum(OJ.test$Purchase != pred.pruned)
misclass.pruned/length(pred.pruned)
## 剪枝前后的测试错误率分别为 0.1666667 和 0.2， 因此剪枝之后的测试错误率更高

8.4.10

  • (a)

    # 10.(a)
library(ISLR)
sum(is.na(Hitters$Salary))
Hitters = Hitters[-which(is.na(Hitters$Salary)), ]
sum(is.na(Hitters$Salary))
Hitters$Salary = log(Hitters$Salary)

    image-20241106225620835

  • (b)

    # 10.(b)
train = 1:200
Hitters.train = Hitters[train, ]
Hitters.test = Hitters[-train, ]

    image-20241106225657752

  • (c)

    # 10.(c)
library(gbm)
set.seed(103)
pows = seq(-10, -0.2, by = 0.1)
lambdas = 10^pows
length.lambdas = length(lambdas)
train.errors = rep(NA, length.lambdas)
test.errors = rep(NA, length.lambdas)
for (i in 1:length.lambdas) {
  boost.hitters = gbm(Salary ~ ., data = Hitters.train, distribution = "gaussian", n.trees = 1000, shrinkage = lambdas[i])
  train.pred = predict(boost.hitters, Hitters.train, n.trees = 1000)
  test.pred = predict(boost.hitters, Hitters.test, n.trees = 1000)
  train.errors[i] = mean((Hitters.train$Salary - train.pred)^2)
  test.errors[i] = mean((Hitters.test$Salary - test.pred)^2)
}
plot(lambdas, train.errors, type = "b", col = "blue", xlab = "Shrinkage", ylab = "Train MSE", pch = 20)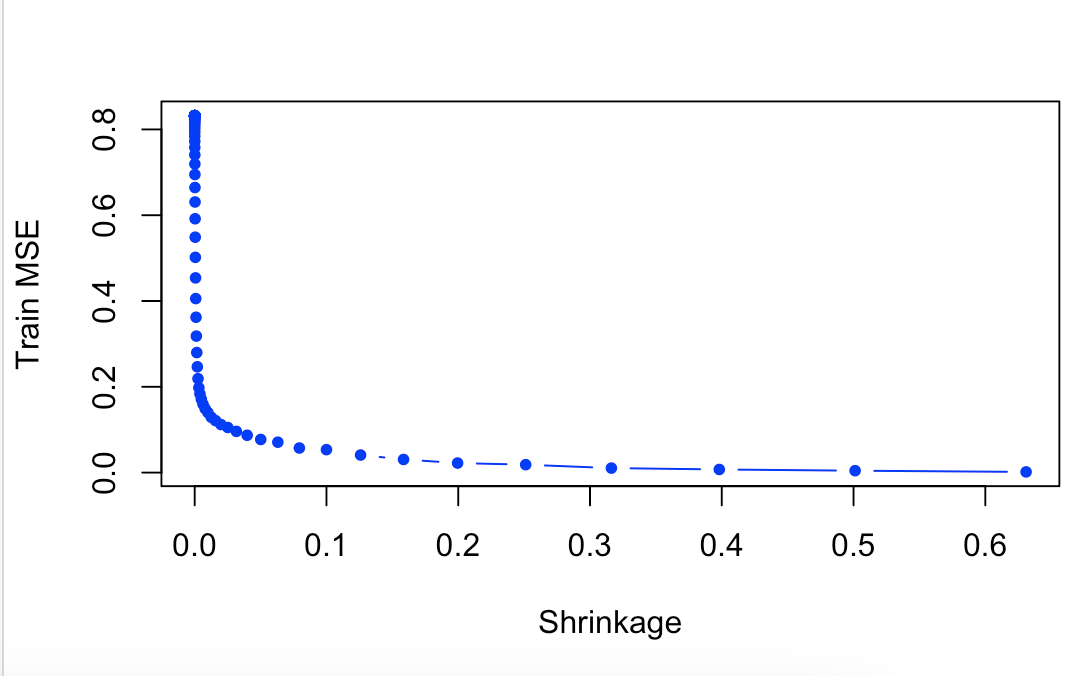

    image-20241106225949856

  • (d)

    # 10.(d)
plot(lambdas, test.errors, type = "b", xlab = "Shrinkage", ylab = "Test MSE", col = "red", pch = 20)
lambdas[which.min(test.errors)]
min(test.errors)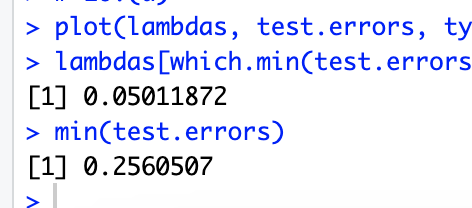

    image-20241106230153077

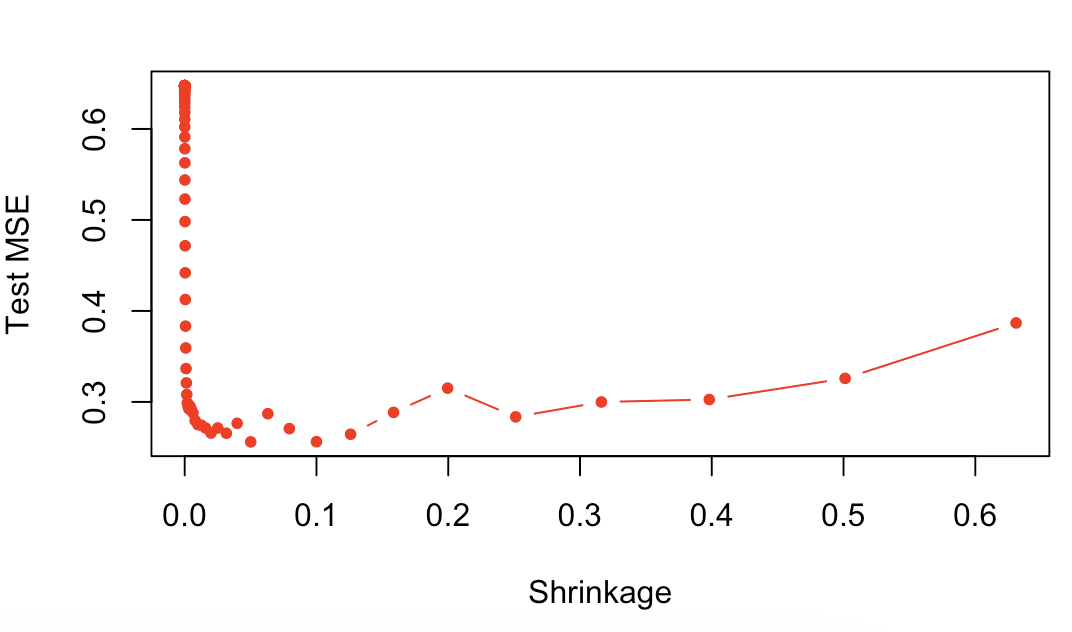
    image-20241106230113540

  • (e)

    # 10.(e)
lm.fit = lm(Salary ~ ., data = Hitters.train)
lm.pred = predict(lm.fit, Hitters.test)
mean((Hitters.test$Salary - lm.pred)^2)
library(glmnet)
set.seed(134)
x = model.matrix(Salary ~ ., data = Hitters.train)
y = Hitters.train$Salary
x.test = model.matrix(Salary ~ ., data = Hitters.test)
lasso.fit = glmnet(x, y, alpha = 1)
lasso.pred = predict(lasso.fit, s = 0.01, newx = x.test)
mean((Hitters.test$Salary - lasso.pred)^2)
## 相较于使用提升法的树模型来说，误差都相对较高

    image-20241106230446186

  • (f)

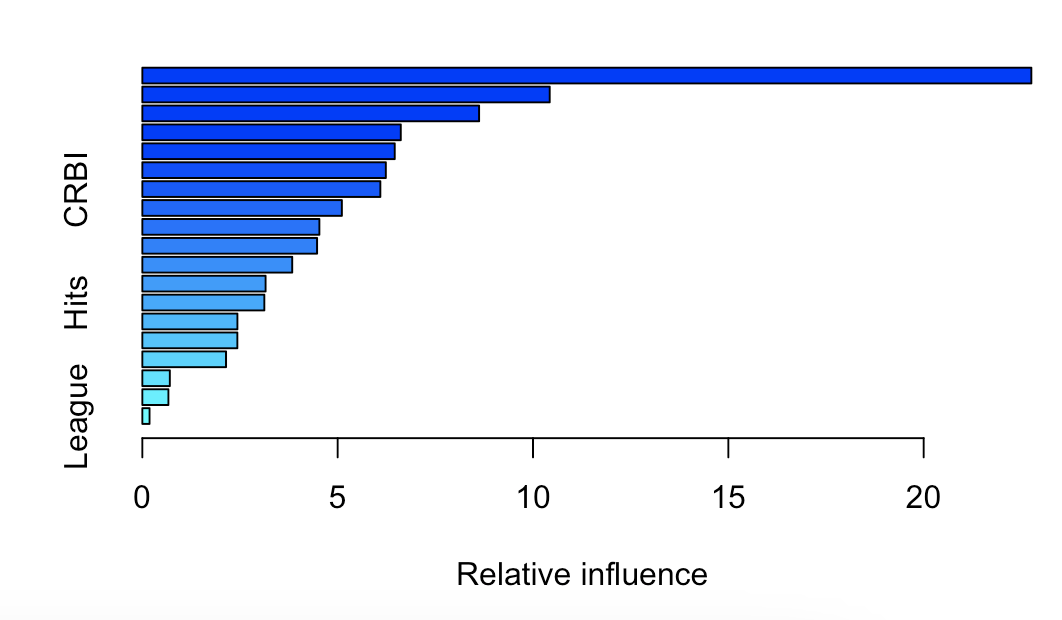
    # 10.(f)
boost.best = gbm(Salary ~ ., data = Hitters.train, distribution = "gaussian", n.trees = 1000, shrinkage = lambdas[which.min(test.errors)])
summary(boost.best)
## CAtBat、CWalks 和 Chits 是最重要的三个变量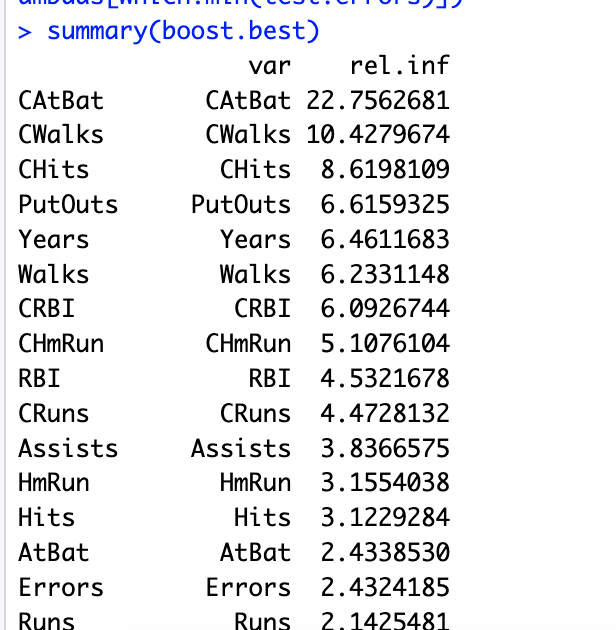

    image-20241106231040724

  • (g)

    # 10.(g)
library(randomForest)
set.seed(21)
rf.hitters = randomForest(Salary ~ ., data = Hitters.train, ntree = 500, mtry = 19)
rf.pred = predict(rf.hitters, Hitters.test)
mean((Hitters.test$Salary - rf.pred)^2)

    image-20241106231250198

  • 完整代码

    # 10.(a)
library(ISLR)
sum(is.na(Hitters$Salary))
Hitters = Hitters[-which(is.na(Hitters$Salary)), ]
sum(is.na(Hitters$Salary))
Hitters$Salary = log(Hitters$Salary)
​
# 10.(b)
train = 1:200
Hitters.train = Hitters[train, ]
Hitters.test = Hitters[-train, ]
​
# 10.(c)
library(gbm)
set.seed(103)
pows = seq(-10, -0.2, by = 0.1)
lambdas = 10^pows
length.lambdas = length(lambdas)
train.errors = rep(NA, length.lambdas)
test.errors = rep(NA, length.lambdas)
for (i in 1:length.lambdas) {
  boost.hitters = gbm(Salary ~ ., data = Hitters.train, distribution = "gaussian", n.trees = 1000, shrinkage = lambdas[i])
  train.pred = predict(boost.hitters, Hitters.train, n.trees = 1000)
  test.pred = predict(boost.hitters, Hitters.test, n.trees = 1000)
  train.errors[i] = mean((Hitters.train$Salary - train.pred)^2)
  test.errors[i] = mean((Hitters.test$Salary - test.pred)^2)
}
plot(lambdas, train.errors, type = "b", col = "blue", xlab = "Shrinkage", ylab = "Train MSE", pch = 20)
​
# 10.(d)
plot(lambdas, test.errors, type = "b", xlab = "Shrinkage", ylab = "Test MSE", col = "red", pch = 20)
lambdas[which.min(test.errors)]
min(test.errors)
​
# 10.(e)
lm.fit = lm(Salary ~ ., data = Hitters.train)
lm.pred = predict(lm.fit, Hitters.test)
mean((Hitters.test$Salary - lm.pred)^2)
library(glmnet)
set.seed(134)
x = model.matrix(Salary ~ ., data = Hitters.train)
y = Hitters.train$Salary
x.test = model.matrix(Salary ~ ., data = Hitters.test)
lasso.fit = glmnet(x, y, alpha = 1)
lasso.pred = predict(lasso.fit, s = 0.01, newx = x.test)
mean((Hitters.test$Salary - lasso.pred)^2)
## 相较于使用提升法的树模型来说，误差都相对较高
​
# 10.(f)
boost.best = gbm(Salary ~ ., data = Hitters.train, distribution = "gaussian", n.trees = 1000, shrinkage = lambdas[which.min(test.errors)])
summary(boost.best)
## CAtBat、CWalks 和 Chits 是最重要的三个变量
​
# 10.(g)
library(randomForest)
set.seed(21)
rf.hitters = randomForest(Salary ~ ., data = Hitters.train, ntree = 500, mtry = 19)
rf.pred = predict(rf.hitters, Hitters.test)
mean((Hitters.test$Salary - rf.pred)^2)

9.7.4

set.seed(131)
x = rnorm(100)
y = 3 * x^2 + 4 + rnorm(100)
train = sample(100, 50)
y[train] = y[train] + 3
y[-train] = y[-train] - 3
plot(x[train], y[train], pch="+", lwd=4, col="red", ylim=c(-4, 20),
     xlab="X", ylab="Y")
points(x[-train], y[-train], pch="o", lwd=4, col="blue")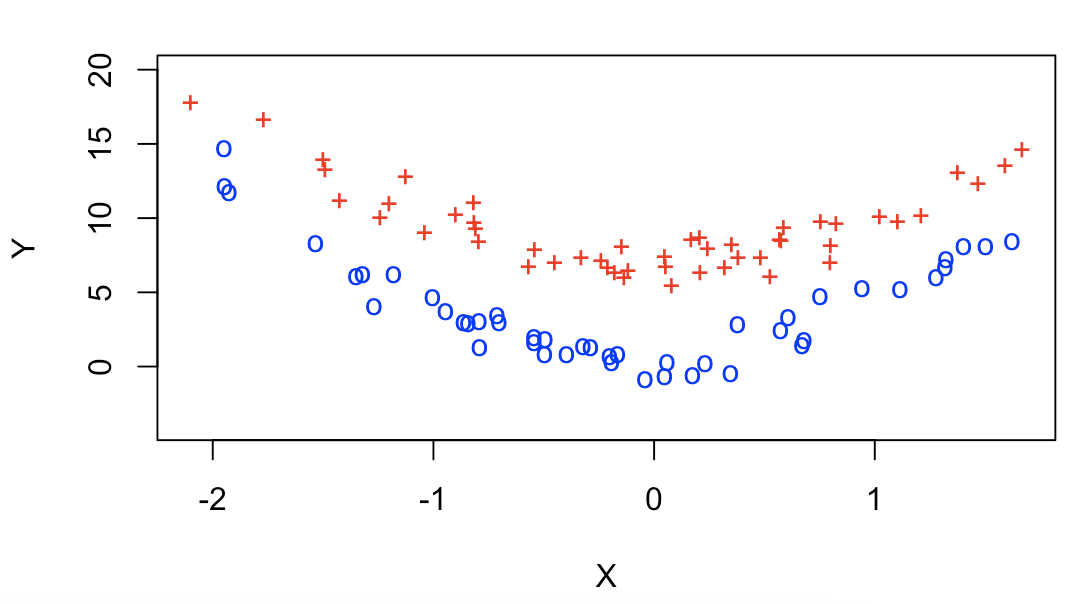

image-20241106231524437

训练集表现：

set.seed(315)
z = rep(0, 100)
z[train] = 1
final.train = c(sample(train, 25), sample(setdiff(1:100, train), 25))
data.train = data.frame(x=x[final.train], y=y[final.train], z=as.factor(z[final.train]))
data.test = data.frame(x=x[-final.train], y=y[-final.train], z=as.factor(z[-final.train]))
library(e1071)
svm.linear = svm(z~., data=data.train, kernel="linear", cost=10)
plot(svm.linear, data.train)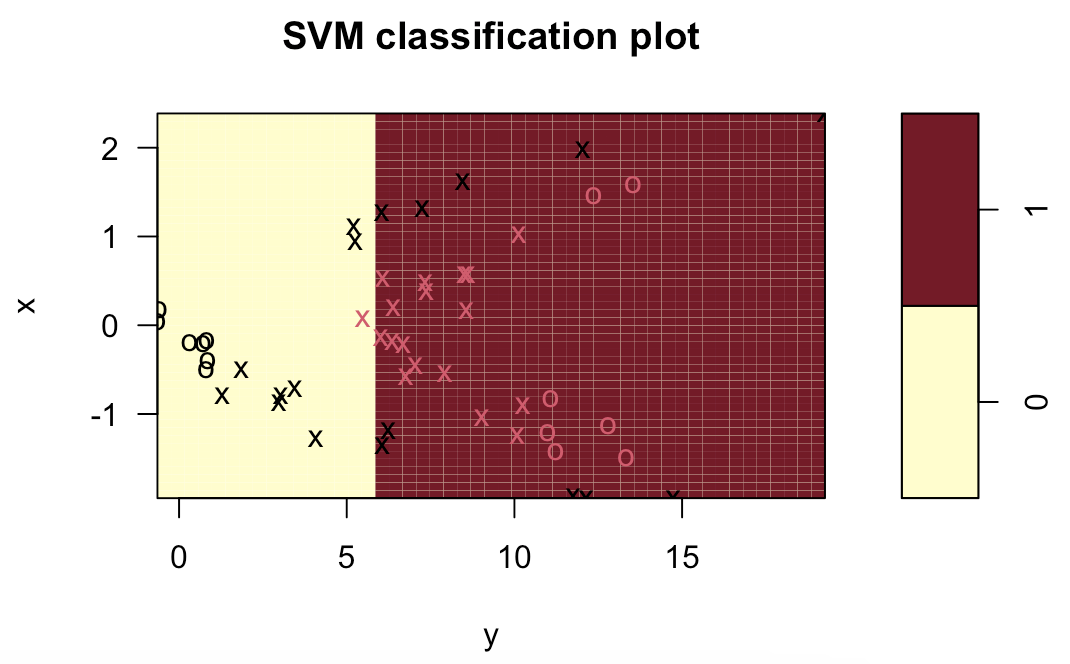

image-20241106231656104

table(z[final.train], predict(svm.linear, data.train))
(10+1)/(15+10+1+24)

image-20241106231734793

set.seed(32545)
svm.poly = svm(z~., data=data.train, kernel="polynomial", cost=10)
plot(svm.poly, data.train)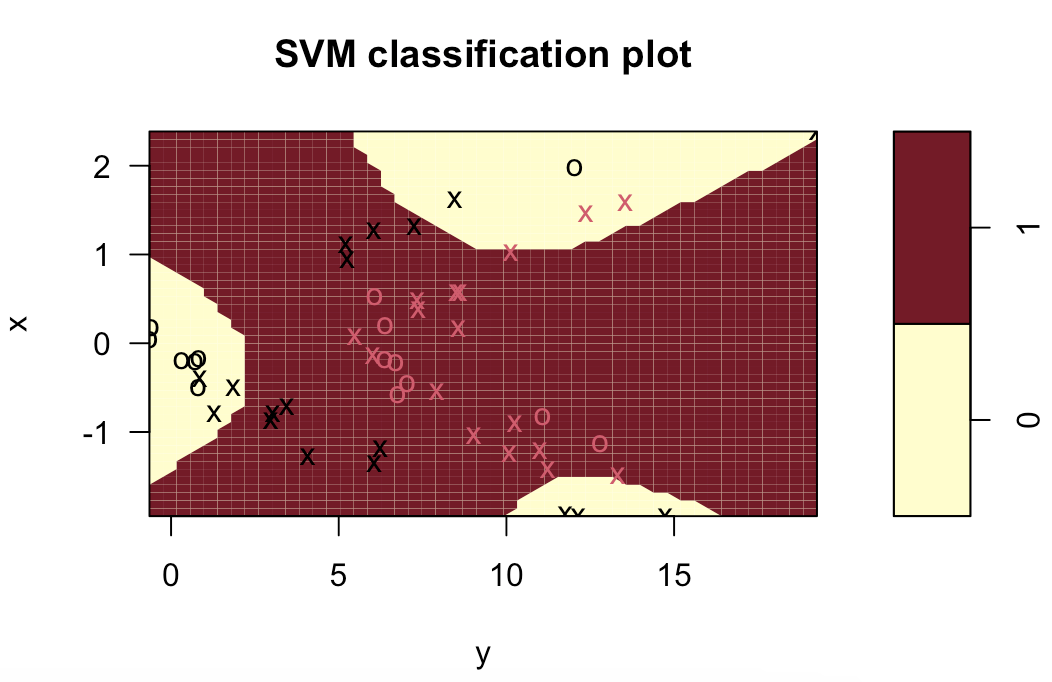

image-20241106232009458

table(z[final.train], predict(svm.poly, data.train))
(10+2)/(15+10+2+23)
set.seed(996)
svm.radial = svm(z~., data=data.train, kernel="radial", gamma=1, cost=10)
plot(svm.radial, data.train)

image-20241106232106000

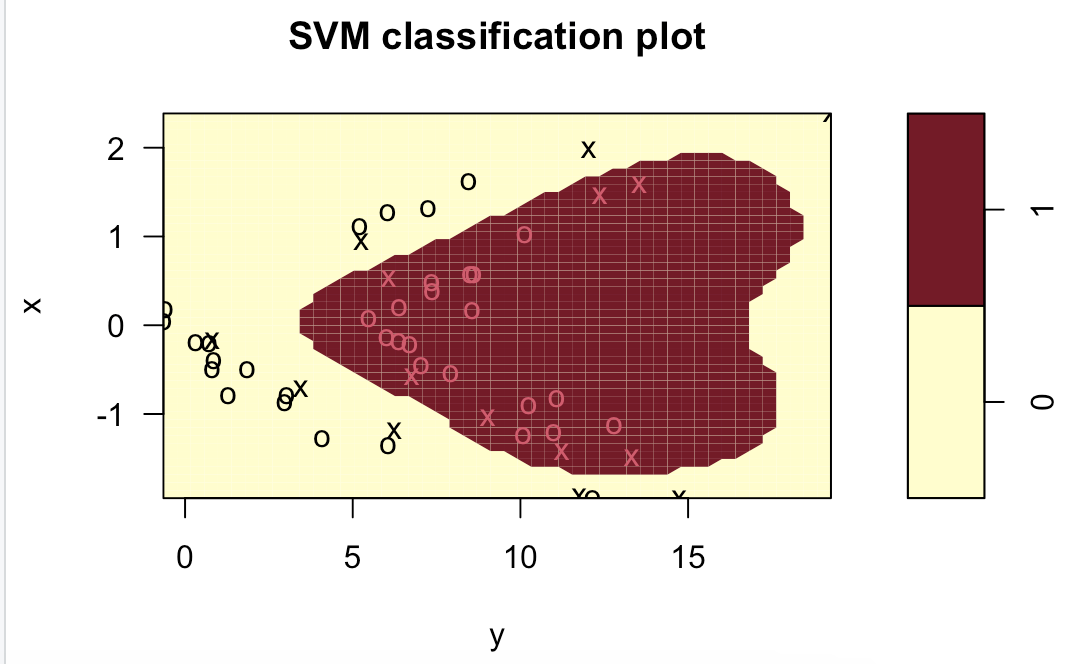
image-20241106232117553

table(z[final.train], predict(svm.radial, data.train))

image-20241106232202833

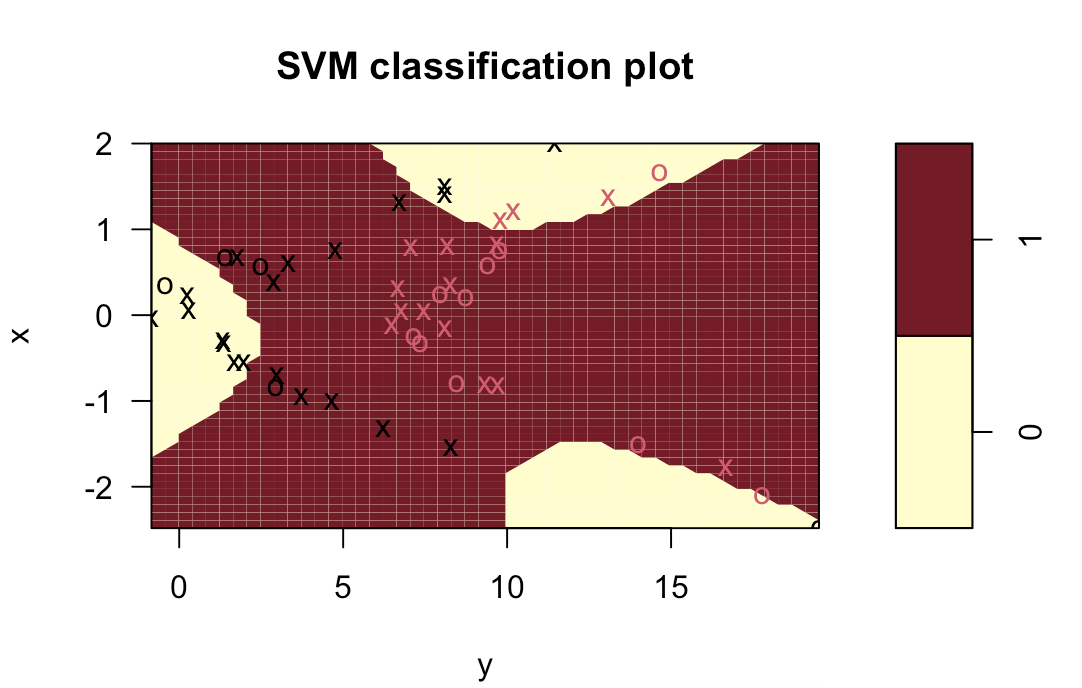
在测试集：

plot(svm.linear, data.test)
table(z[-final.train], predict(svm.linear, data.test))
7/(7+18+25)
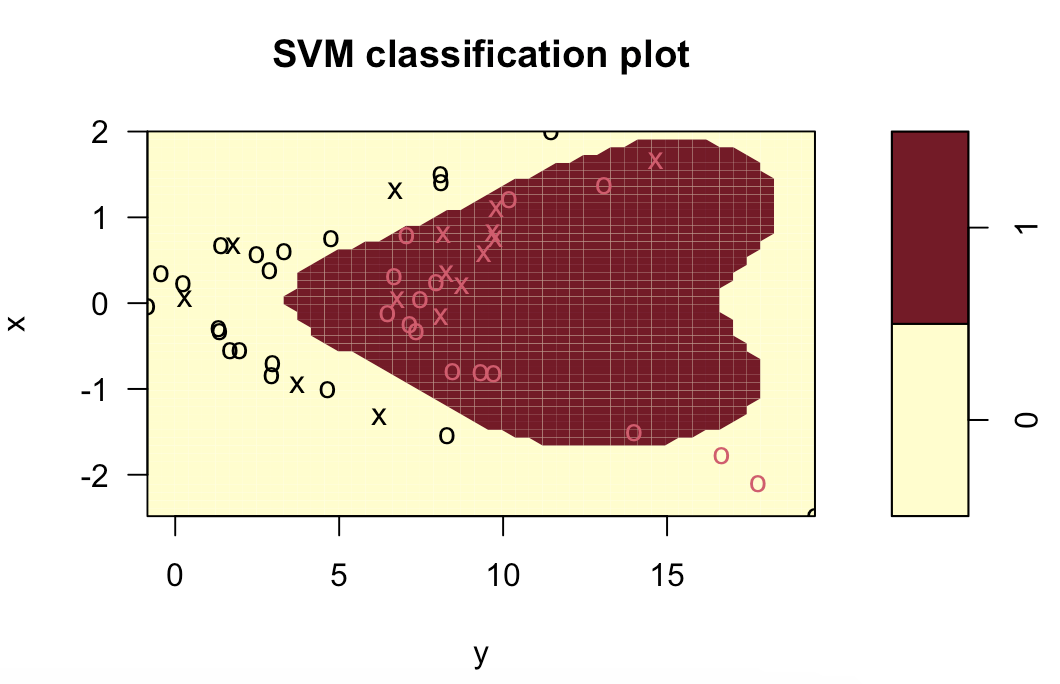
plot(svm.poly, data.test)
table(z[-final.train], predict(svm.poly, data.test))
(13+4)/(12+13+4+21)
plot(svm.radial, data.test)
table(z[-final.train], predict(svm.radial, data.test))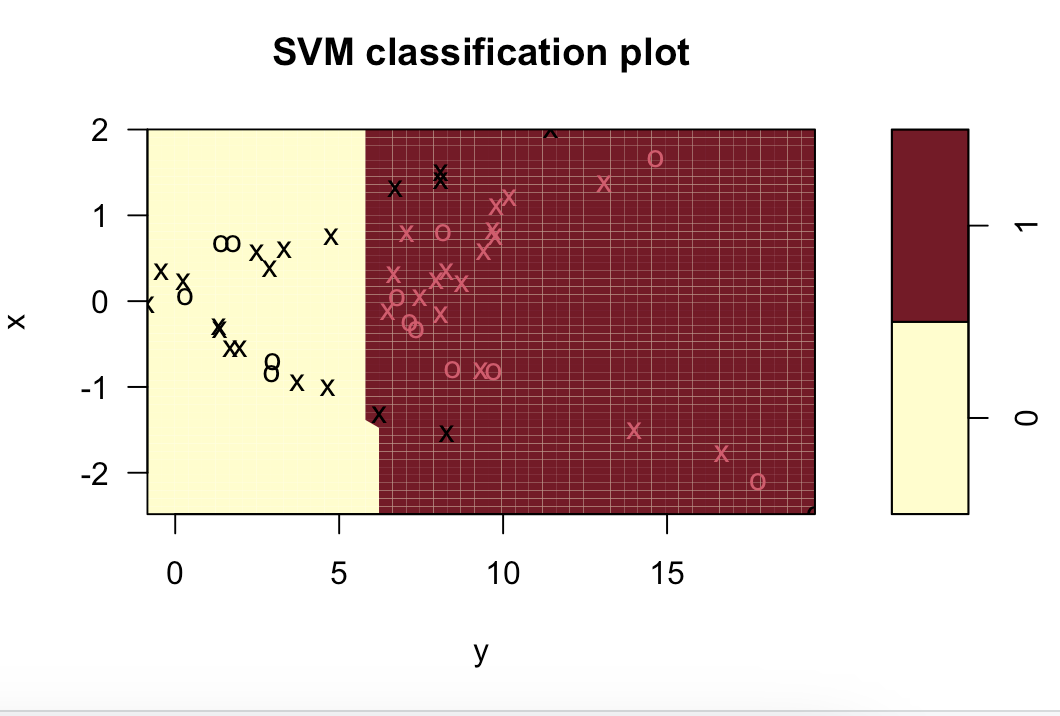

image-20241106232523624

image-20241106232543044

image-20241106232602818

image-20241106232717987

  • 完整代码

    set.seed(131)
x = rnorm(100)
y = 3 * x^2 + 4 + rnorm(100)
train = sample(100, 50)
y[train] = y[train] + 3
y[-train] = y[-train] - 3
plot(x[train], y[train], pch="+", lwd=4, col="red", ylim=c(-4, 20),
     xlab="X", ylab="Y")
points(x[-train], y[-train], pch="o", lwd=4, col="blue")
​
set.seed(315)
z = rep(0, 100)
z[train] = 1
final.train = c(sample(train, 25), sample(setdiff(1:100, train), 25))
data.train = data.frame(x=x[final.train], y=y[final.train], z=as.factor(z[final.train]))
data.test = data.frame(x=x[-final.train], y=y[-final.train], z=as.factor(z[-final.train]))
library(e1071)
svm.linear = svm(z~., data=data.train, kernel="linear", cost=10)
plot(svm.linear, data.train)
​
table(z[final.train], predict(svm.linear, data.train))
(10+1)/(15+10+1+24)
​
set.seed(32545)
svm.poly = svm(z~., data=data.train, kernel="polynomial", cost=10)
plot(svm.poly, data.train)
​
table(z[final.train], predict(svm.poly, data.train))
(10+2)/(15+10+2+23)
set.seed(996)
svm.radial = svm(z~., data=data.train, kernel="radial", gamma=1, cost=10)
plot(svm.radial, data.train)
​
table(z[final.train], predict(svm.radial, data.train))
​
plot(svm.linear, data.test)
table(z[-final.train], predict(svm.linear, data.test))
7/(7+18+25)
plot(svm.poly, data.test)
table(z[-final.train], predict(svm.poly, data.test))
(13+4)/(12+13+4+21)
plot(svm.radial, data.test)
table(z[-final.train], predict(svm.radial, data.test))

9.7.5

  • (a)

    # 5.(a)
set.seed(421)
x1 = runif(500) - 0.5
x2 = runif(500) - 0.5
y = 1 * (x1^2 - x2^2 > 0)

    image-20241106234114159

  • (b)

    # 5.(b)
plot(x1[y == 0], x2[y == 0], col = "red", xlab = "X1", ylab = "X2", pch = "+")
points(x1[y == 1], x2[y == 1], col = "blue", pch = 4)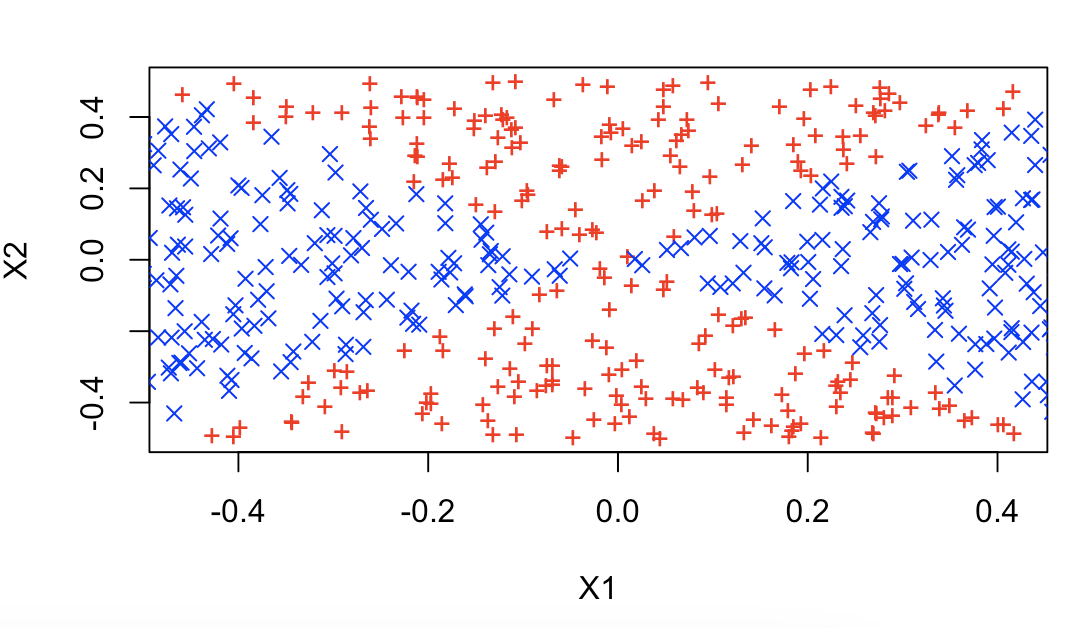

    image-20241106234356156

  • (c)

    # 5.(c)
lm.fit = glm(y ~ x1 + x2, family = binomial)
summary(lm.fit)
## p 值较大，和 x1、x2 之间存在的关系并不显著。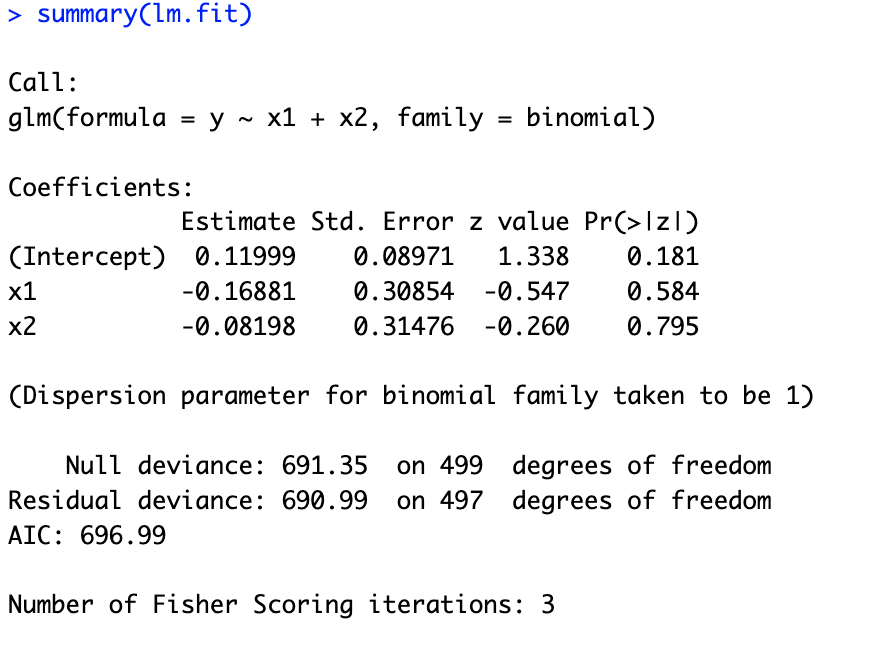

    image-20241106235236751

  • (d)

    # 5.(d)
data = data.frame(x1 = x1, x2 = x2, y = y)
lm.prob = predict(lm.fit, data, type = "response")
lm.pred = ifelse(lm.prob > 0.52, 1, 0)
data.pos = data[lm.pred == 1, ]
data.neg = data[lm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)
## 在给定模型和概率阈值为 0.5 的情况下， 无法显示决策边界。 我们将概率阈值移至 0.52，以显示有意义的决策边界。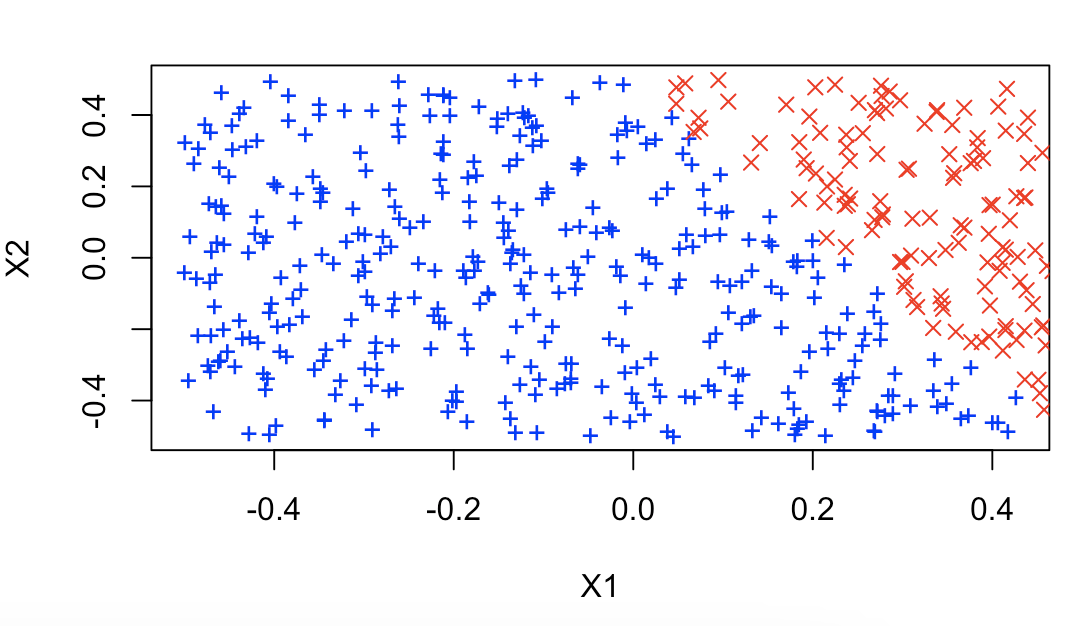

    image-20241106235547293

  • (e)

    # 5.(e)
lm.fit = glm(y ~ poly(x1, 2) + poly(x2, 2) + I(x1 * x2), data = data, family = binomial)

  • (f)

    # 5.(f)
lm.prob = predict(lm.fit, data, type = "response")
lm.pred = ifelse(lm.prob > 0.5, 1, 0)
data.pos = data[lm.pred == 1, ]
data.neg = data[lm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)

    image-20241106235857486

  • (g)

    # 5.(g)
library(e1071)
svm.fit = svm(as.factor(y) ~ x1 + x2, data, kernel = "linear", cost = 0.1)
svm.pred = predict(svm.fit, data)
data.pos = data[svm.pred == 1, ]
data.neg = data[svm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)
## 当我们使用线性核函数进行预测时，无法将各个类别之间区分开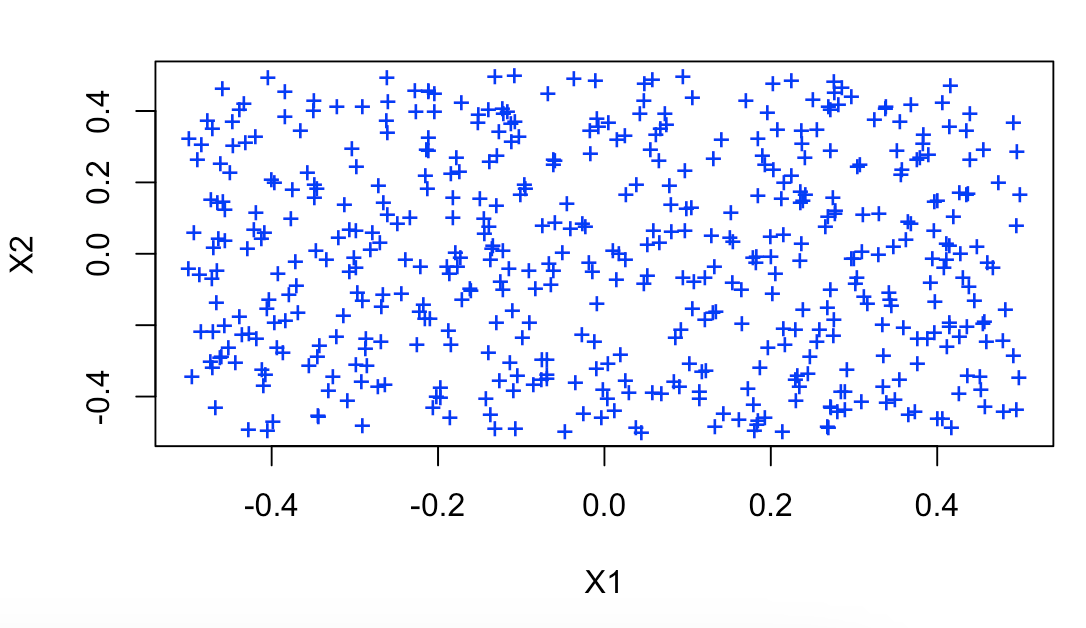

    image-20241107000127852

  • (h)

    # 5.(h)
svm.fit = svm(as.factor(y) ~ x1 + x2, data, gamma = 1)
svm.pred = predict(svm.fit, data)
data.pos = data[svm.pred == 1, ]
data.neg = data[svm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)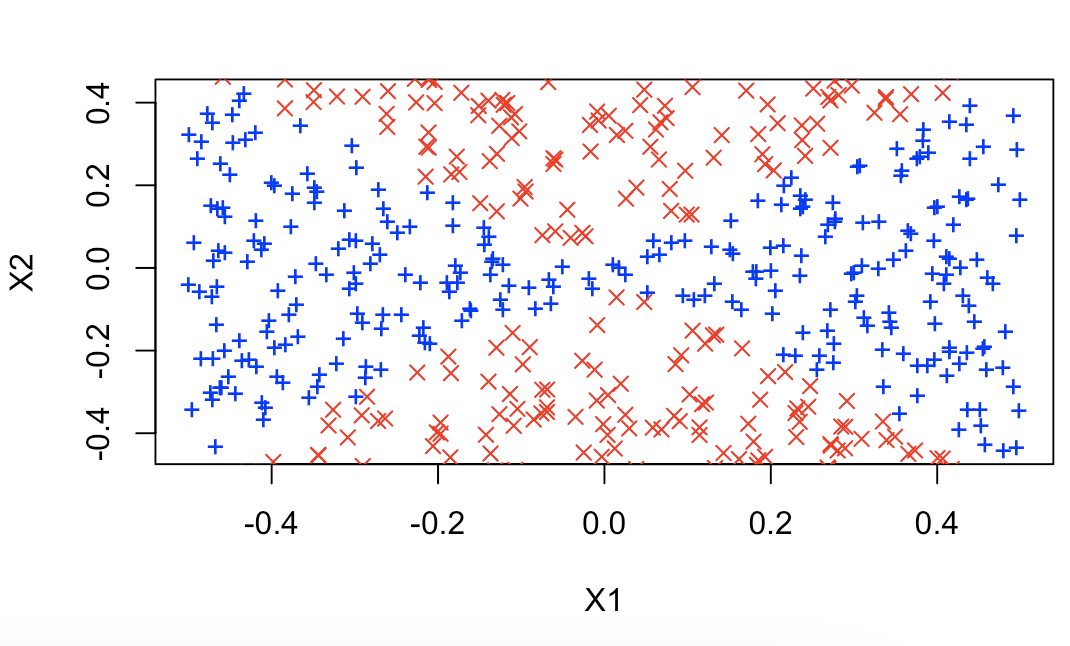

    image-20241107000333670

  • (i)

    # 5.(i)
## 这个实验展示了一个重要的观点：使用非线性核的 SVM 在识别非线性决策边界方面具有显著优势。
## 相比之下，没有交互项的逻辑回归模型和仅使用线性核的 SVM 难以捕捉到这样的边界。
## 虽然在逻辑回归中加入交互项可以提升模型的拟合能力，使其与径向基核的 SVM 相媲美，
## 但这需要手动选择和调整交互项，这在特征数量众多的情况下会非常耗时且复杂。
## 相比之下，径向基核 SVM 只需调整一个参数——gamma
## 并且这个参数可以通过交叉验证来优化，使得模型选择过程更加简便和高效。

  • 完整代码

    # 5.(a)
set.seed(421)
x1 = runif(500) - 0.5
x2 = runif(500) - 0.5
y = 1 * (x1^2 - x2^2 > 0)
​
# 5.(b)
plot(x1[y == 0], x2[y == 0], col = "red", xlab = "X1", ylab = "X2", pch = "+")
points(x1[y == 1], x2[y == 1], col = "blue", pch = 4)
​
# 5.(c)
lm.fit = glm(y ~ x1 + x2, family = binomial)
summary(lm.fit)
## p 值较大，和 x1、x2 之间存在的关系并不显著。
​
# 5.(d)
data = data.frame(x1 = x1, x2 = x2, y = y)
lm.prob = predict(lm.fit, data, type = "response")
lm.pred = ifelse(lm.prob > 0.52, 1, 0)
data.pos = data[lm.pred == 1, ]
data.neg = data[lm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)
## 在给定模型和概率阈值为 0.5 的情况下， 无法显示决策边界。 我们将概率阈值移至 0.52，以显示有意义的决策边界。
​
# 5.(e)
lm.fit = glm(y ~ poly(x1, 2) + poly(x2, 2) + I(x1 * x2), data = data, family = binomial)
​
# 5.(f)
lm.prob = predict(lm.fit, data, type = "response")
lm.pred = ifelse(lm.prob > 0.5, 1, 0)
data.pos = data[lm.pred == 1, ]
data.neg = data[lm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)
​
# 5.(g)
library(e1071)
svm.fit = svm(as.factor(y) ~ x1 + x2, data, kernel = "linear", cost = 0.1)
svm.pred = predict(svm.fit, data)
data.pos = data[svm.pred == 1, ]
data.neg = data[svm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)
## 当我们使用线性核函数进行预测时，无法将各个类别之间区分开
​
# 5.(h)
svm.fit = svm(as.factor(y) ~ x1 + x2, data, gamma = 1)
svm.pred = predict(svm.fit, data)
data.pos = data[svm.pred == 1, ]
data.neg = data[svm.pred == 0, ]
plot(data.pos$x1, data.pos$x2, col = "blue", xlab = "X1", ylab = "X2", pch = "+")
points(data.neg$x1, data.neg$x2, col = "red", pch = 4)
​
# 5.(i)
## 这个实验展示了一个重要的观点：使用非线性核的 SVM 在识别非线性决策边界方面具有显著优势。
## 相比之下，没有交互项的逻辑回归模型和仅使用线性核的 SVM 难以捕捉到这样的边界。
## 虽然在逻辑回归中加入交互项可以提升模型的拟合能力，使其与径向基核的 SVM 相媲美，
## 但这需要手动选择和调整交互项，这在特征数量众多的情况下会非常耗时且复杂。
## 相比之下，径向基核 SVM 只需调整一个参数——gamma
## 并且这个参数可以通过交叉验证来优化，使得模型选择过程更加简便和高效。

9.7.6

  • (a)

    # 6.(a)
set.seed(3154)
x.one = runif(500, 0, 90)
y.one = runif(500, x.one + 10, 100)
x.one.noise = runif(50, 20, 80)
y.one.noise = 5/4 * (x.one.noise - 10) + 0.1
x.zero = runif(500, 10, 100)
y.zero = runif(500, 0, x.zero - 10)
x.zero.noise = runif(50, 20, 80)
y.zero.noise = 5/4 * (x.zero.noise - 10) - 0.1
class.one = seq(1, 550)
x = c(x.one, x.one.noise, x.zero, x.zero.noise)
y = c(y.one, y.one.noise, y.zero, y.zero.noise)
plot(x[class.one], y[class.one], col = "blue", pch = "+", ylim = c(0, 100))
points(x[-class.one], y[-class.one], col = "red", pch = 4)
## 分界：5x–4y–50 = 0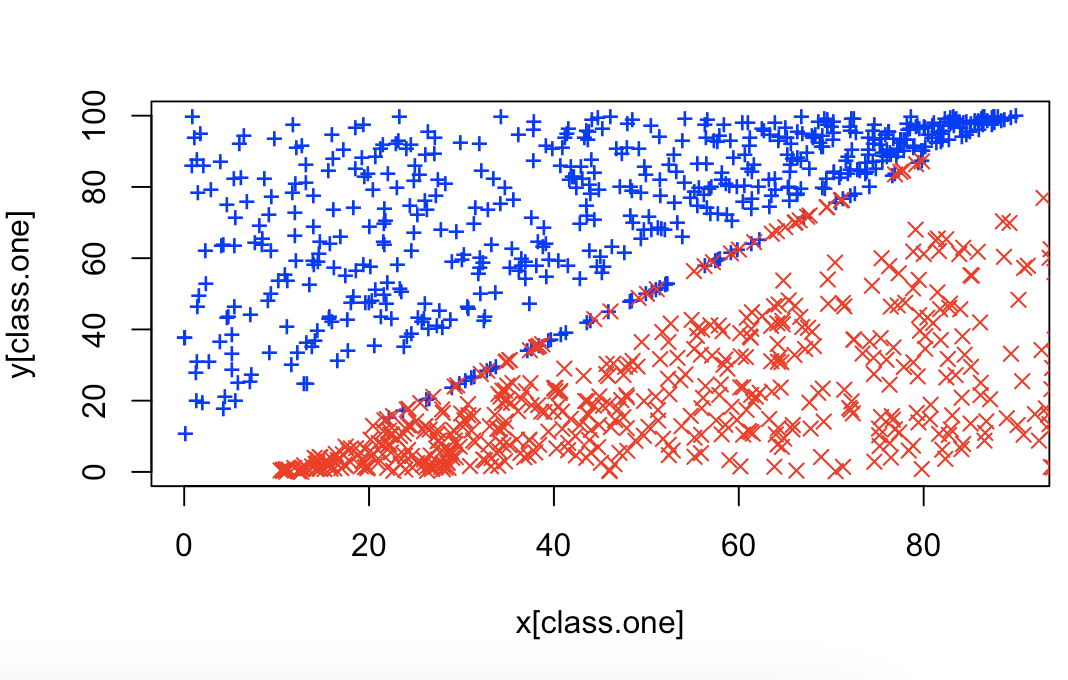

    image-20241107001139805

  • (b)

    # 6.(b)
library(e1071)
set.seed(555)
z = rep(0, 1100)
z[class.one] = 1
data = data.frame(x = x, y = y, z = z)
tune.out = tune(svm, as.factor(z) ~ ., data = data, kernel = "linear",
                ranges = list(cost = c(0.01, 0.1, 1, 5, 10, 100, 1000, 10000)))
summary(tune.out)
data.frame(cost = tune.out$performances$cost, misclass = tune.out$performances$error * 1100)
## 当 cost=10000 时，所有的点都能够被正确分类。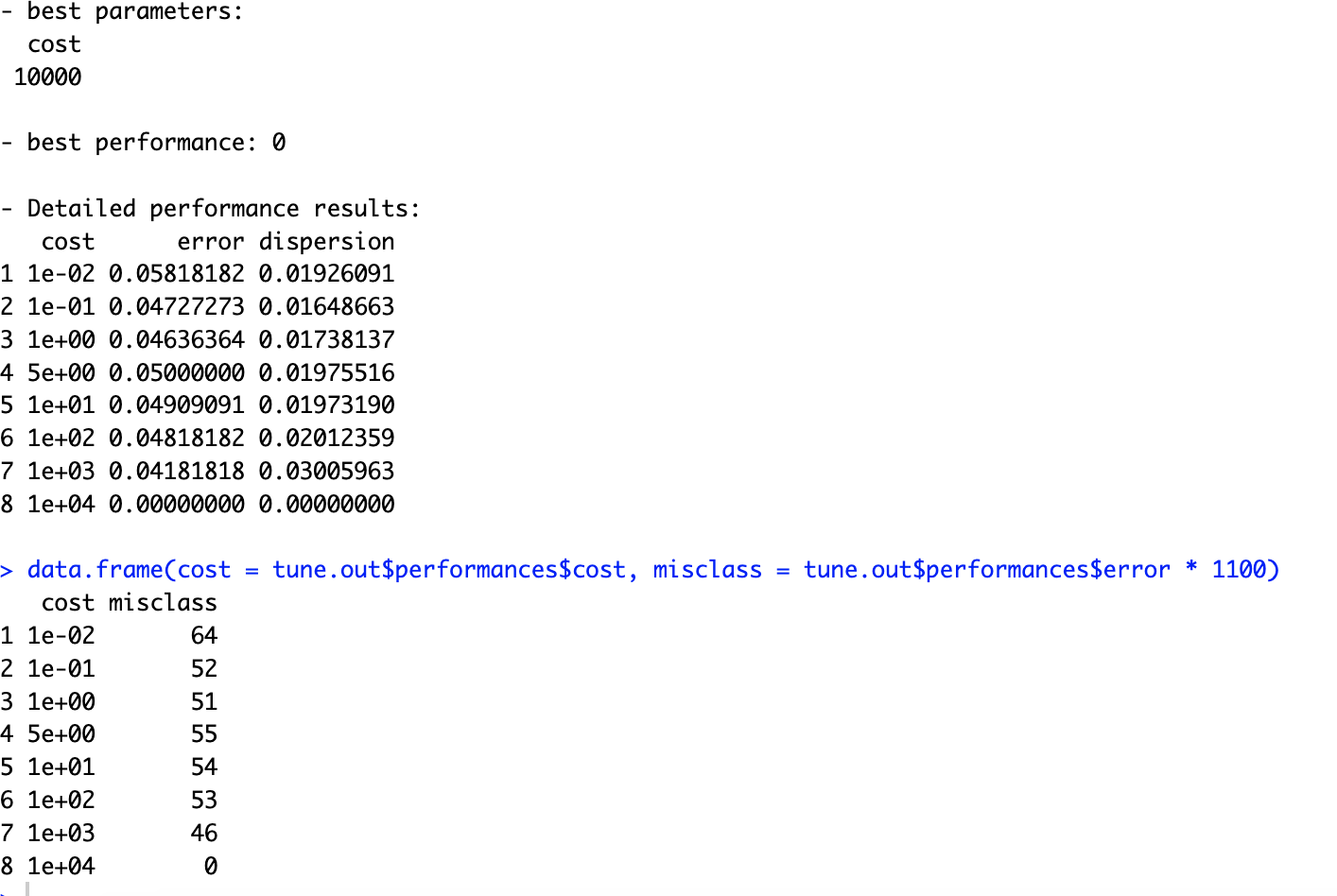

    image-20241107002243197

  • (c)

    # 6.(c)
set.seed(1111)
x.test = runif(1000, 0, 100)
class.one = sample(1000, 500)
y.test = rep(NA, 1000)
for (i in class.one) {
  y.test[i] = runif(1, x.test[i], 100)
}
for (i in setdiff(1:1000, class.one)) {
  y.test[i] = runif(1, 0, x.test[i])
}
plot(x.test[class.one], y.test[class.one], col = "blue", pch = "+")
points(x.test[-class.one], y.test[-class.one], col = "red", pch = 4)
set.seed(30012)
z.test = rep(0, 1000)
z.test[class.one] = 1
all.costs = c(0.01, 0.1, 1, 5, 10, 100, 1000, 10000)
test.errors = rep(NA, 8)
data.test = data.frame(x = x.test, y = y.test, z = z.test)
for (i in 1:length(all.costs)) {
  svm.fit = svm(as.factor(z) ~ ., data = data, kernel = "linear", cost = all.costs[i])
  svm.predict = predict(svm.fit, data.test)
  test.errors[i] = sum(svm.predict != data.test$z)
}
data.frame(cost = all.costs, `test misclass` = test.errors)
## 当 cost=5 或 cost=10 时，误分数目最少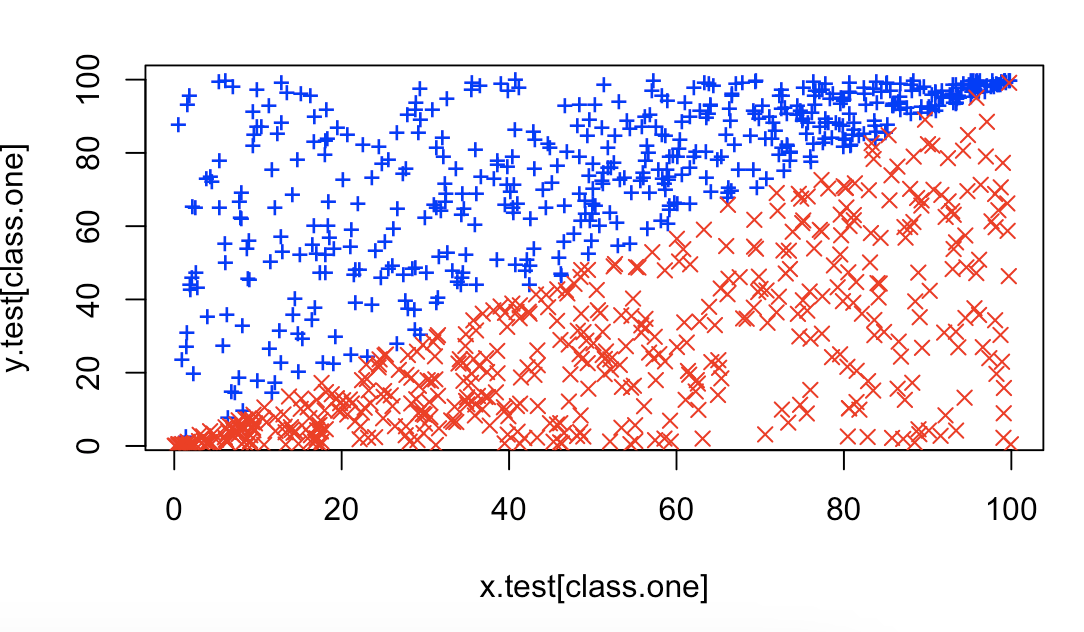

    image-20241107002414494

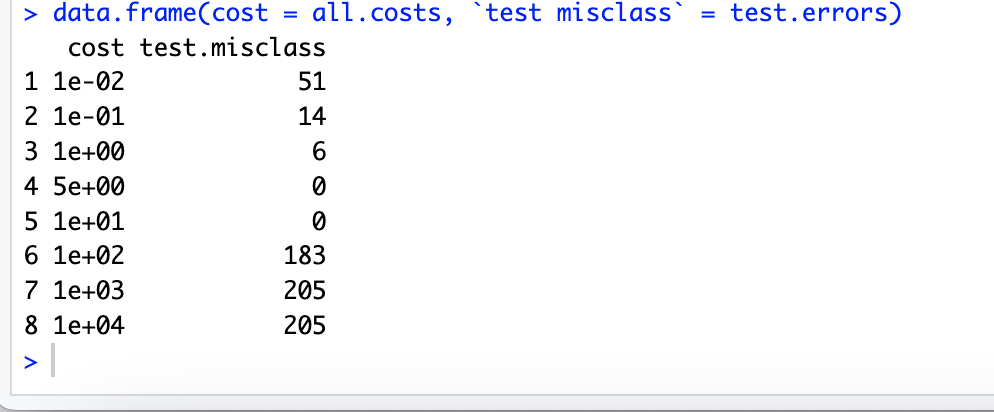
    image-20241107002515439

  • (d)

    # 6.(d)
## 观察到线性核的过拟合现象。当代价参数较大时，模型试图精确地对训练数据中的噪声点进行分类
## 导致对训练数据的过度拟合。然而，当代价参数较小时，模型在噪声测试点上可能会犯一些错误
## 但在测试数据上的表现却更加优异。

  • 完整代码

    # 6.(a)
set.seed(3154)
x.one = runif(500, 0, 90)
y.one = runif(500, x.one + 10, 100)
x.one.noise = runif(50, 20, 80)
y.one.noise = 5/4 * (x.one.noise - 10) + 0.1
x.zero = runif(500, 10, 100)
y.zero = runif(500, 0, x.zero - 10)
x.zero.noise = runif(50, 20, 80)
y.zero.noise = 5/4 * (x.zero.noise - 10) - 0.1
class.one = seq(1, 550)
x = c(x.one, x.one.noise, x.zero, x.zero.noise)
y = c(y.one, y.one.noise, y.zero, y.zero.noise)
plot(x[class.one], y[class.one], col = "blue", pch = "+", ylim = c(0, 100))
points(x[-class.one], y[-class.one], col = "red", pch = 4)
## 分界：5x–4y–50 = 0
​
# 6.(b)
library(e1071)
set.seed(555)
z = rep(0, 1100)
z[class.one] = 1
data = data.frame(x = x, y = y, z = z)
tune.out = tune(svm, as.factor(z) ~ ., data = data, kernel = "linear",
                ranges = list(cost = c(0.01, 0.1, 1, 5, 10, 100, 1000, 10000)))
summary(tune.out)
data.frame(cost = tune.out$performances$cost, misclass = tune.out$performances$error * 1100)
## 当 cost=10000 时，所有的点都能够被正确分类。
​
# 6.(c)
set.seed(1111)
x.test = runif(1000, 0, 100)
class.one = sample(1000, 500)
y.test = rep(NA, 1000)
for (i in class.one) {
  y.test[i] = runif(1, x.test[i], 100)
}
for (i in setdiff(1:1000, class.one)) {
  y.test[i] = runif(1, 0, x.test[i])
}
plot(x.test[class.one], y.test[class.one], col = "blue", pch = "+")
points(x.test[-class.one], y.test[-class.one], col = "red", pch = 4)
set.seed(30012)
z.test = rep(0, 1000)
z.test[class.one] = 1
all.costs = c(0.01, 0.1, 1, 5, 10, 100, 1000, 10000)
test.errors = rep(NA, 8)
data.test = data.frame(x = x.test, y = y.test, z = z.test)
for (i in 1:length(all.costs)) {
  svm.fit = svm(as.factor(z) ~ ., data = data, kernel = "linear", cost = all.costs[i])
  svm.predict = predict(svm.fit, data.test)
  test.errors[i] = sum(svm.predict != data.test$z)
}
data.frame(cost = all.costs, `test misclass` = test.errors)
## 当 cost=5 或 cost=10 时，误分数目最少
​
# 6.(d)
## 观察到线性核的过拟合现象。当代价参数较大时，模型试图精确地对训练数据中的噪声点进行分类
## 导致对训练数据的过度拟合。然而，当代价参数较小时，模型在噪声测试点上可能会犯一些错误
## 但在测试数据上的表现却更加优异。

9.7.7

  • (a)

    # 7.(a)
library(ISLR)
gas.med = median(Auto$mpg)
new.var = ifelse(Auto$mpg > gas.med, 1, 0)
Auto$mpglevel = as.factor(new.var)

  • (b)

    # 7.(b)
library(e1071)
set.seed(3255)
tune.out = tune(svm, mpglevel ~ ., data = Auto, kernel = "linear", ranges = list(cost = c(0.01, 0.1, 1, 5, 10, 100)))
summary(tune.out)
## 从结果可以看出：当采用 10 折交叉验证，当 cost=1 时，error 最小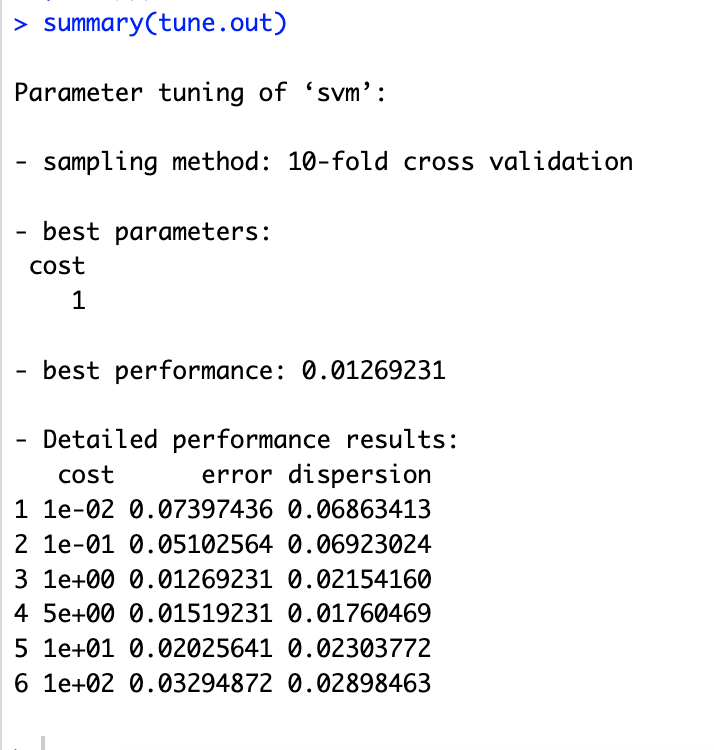

    image-20241107002938947

  • (c)

    # 7.(c)
### 多项式核函数
set.seed(21)
tune.out = tune(svm, mpglevel ~ ., data = Auto, kernel = "polynomial", ranges = list(cost = c(0.1, 1, 5, 10), degree = c(2, 3, 4)))
summary(tune.out)
## 当 cost=10,degree=2 时，error 最小。
### 径向核函数
set.seed(463)
tune.out = tune(svm, mpglevel ~ ., data = Auto, kernel = "radial", ranges = list(cost = c(0.1, 1, 5, 10), gamma = c(0.01, 0.1, 1, 5, 10, 100)))
summary(tune.out)
## 当 cost=10,gamma=0.01 时，error 最小

  • (d)

    # 9.(d)
### 线性模型
svm.linear = svm(mpglevel ~ ., data = Auto, kernel = "linear", cost = 1)
svm.poly = svm(mpglevel ~ ., data = Auto, kernel = "polynomial", cost = 10, degree = 2)
svm.radial = svm(mpglevel ~ ., data = Auto, kernel = "radial", cost = 10, gamma = 0.01)
plotpairs = function(fit) {
  for (name in names(Auto)[!(names(Auto) %in% c("mpg", "mpglevel", "name"))]) {
    plot(fit, Auto, as.formula(paste("mpg~", name, sep = "")))
  }
}
plotpairs(svm.linear)
plotpairs(svm.poly)
plotpairs(svm.radial)
​

    线性：

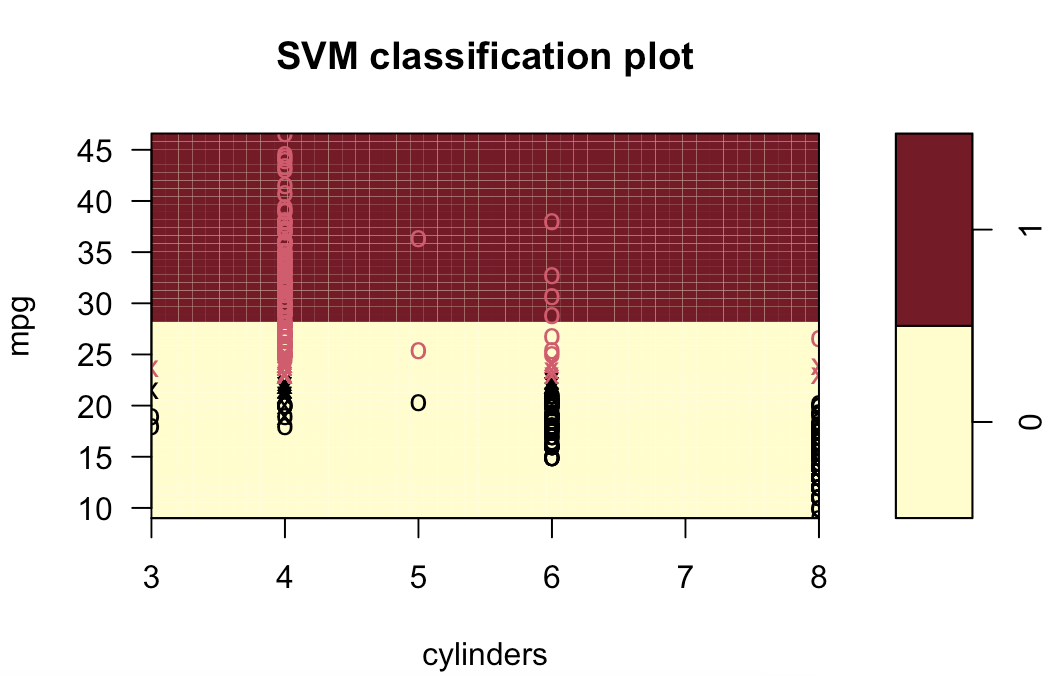
    image-20241107004409226

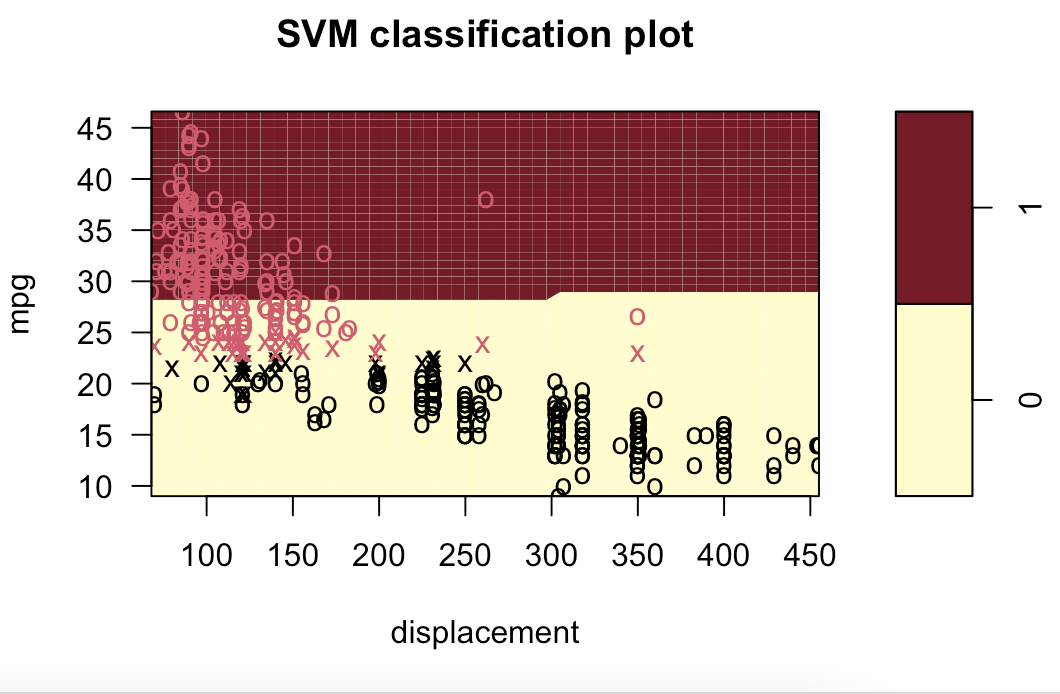
    image-20241107004418478

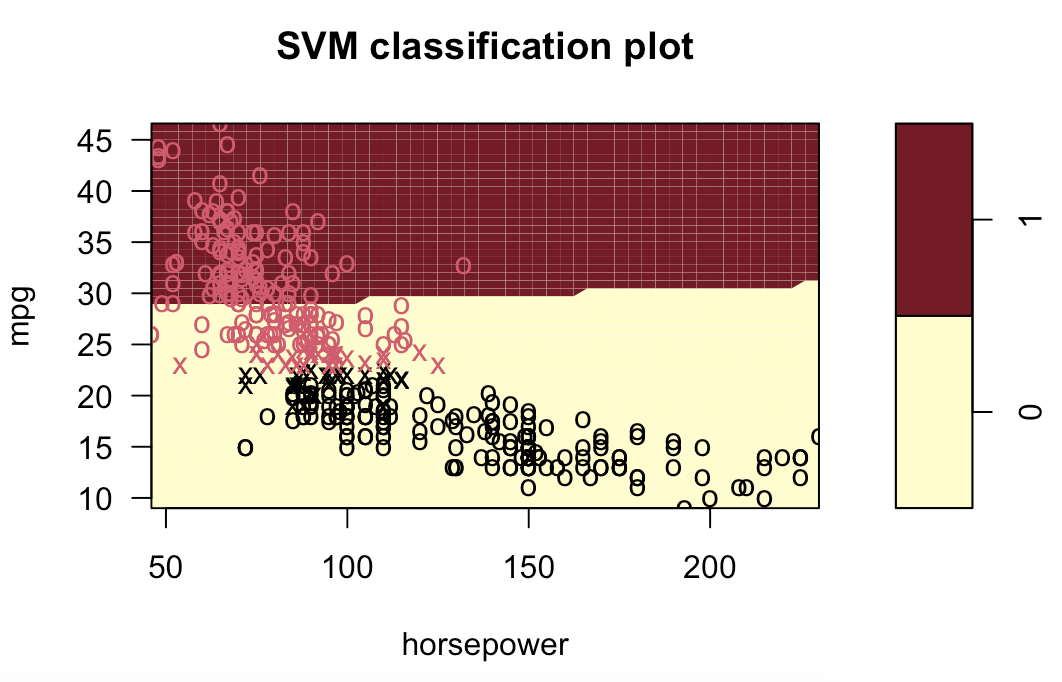
    image-20241107004427588

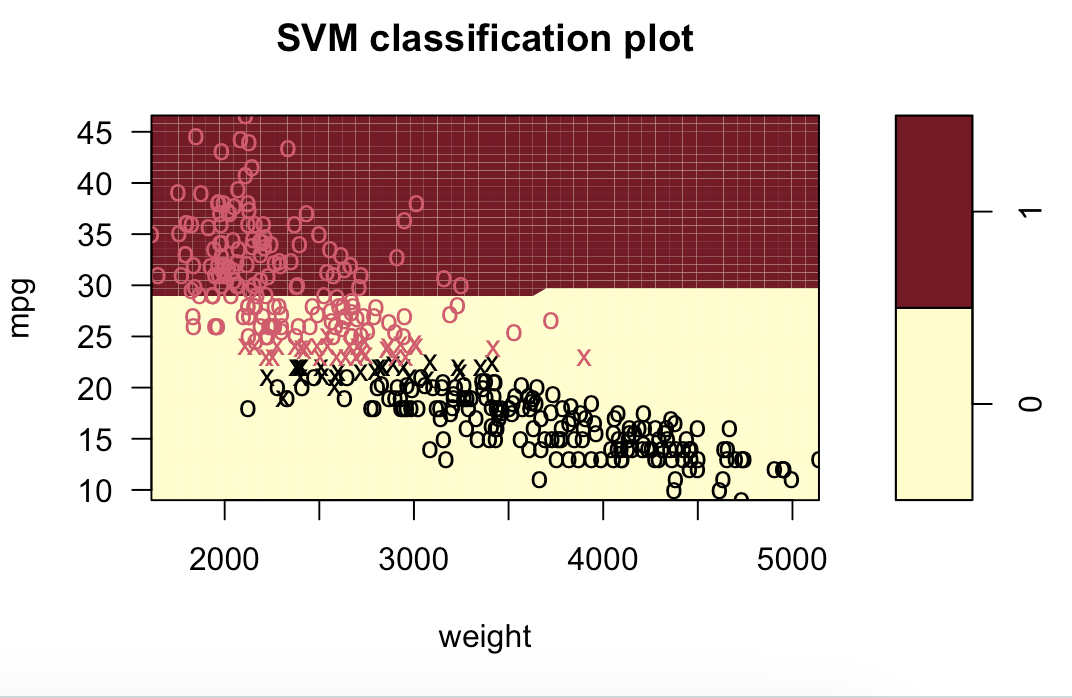
    image-20241107004439503

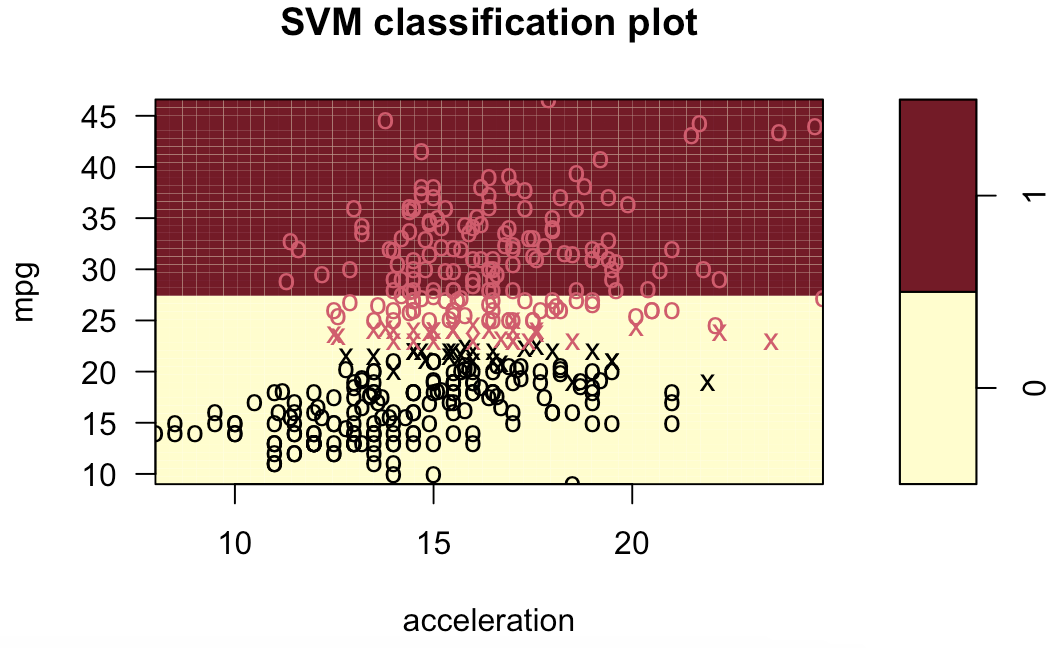
    image-20241107004450961

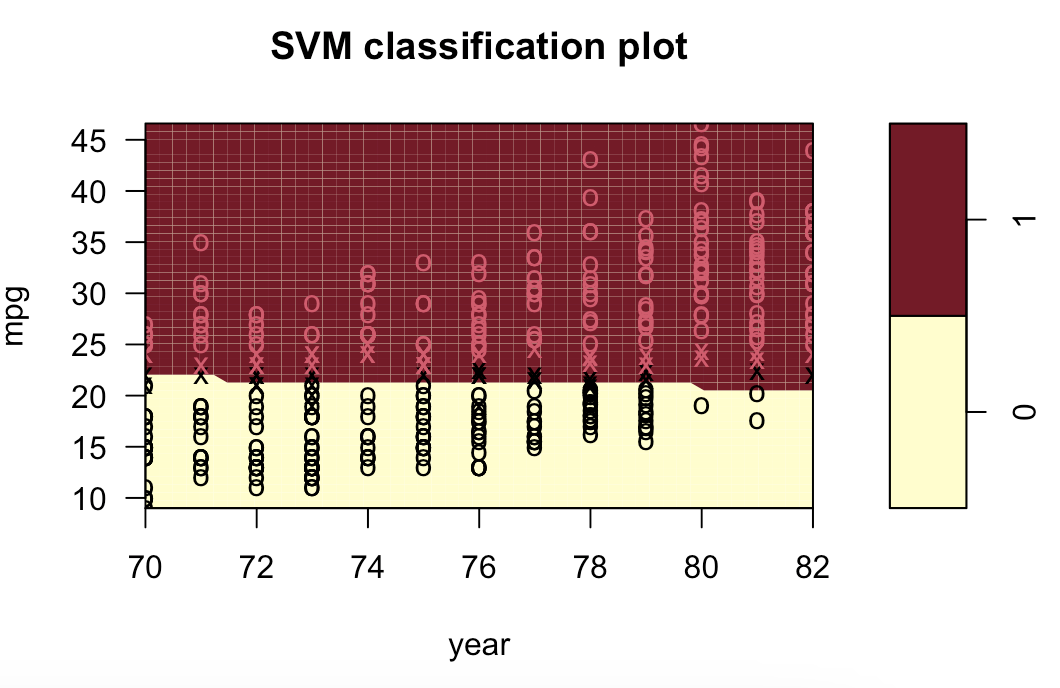
    image-20241107004501000

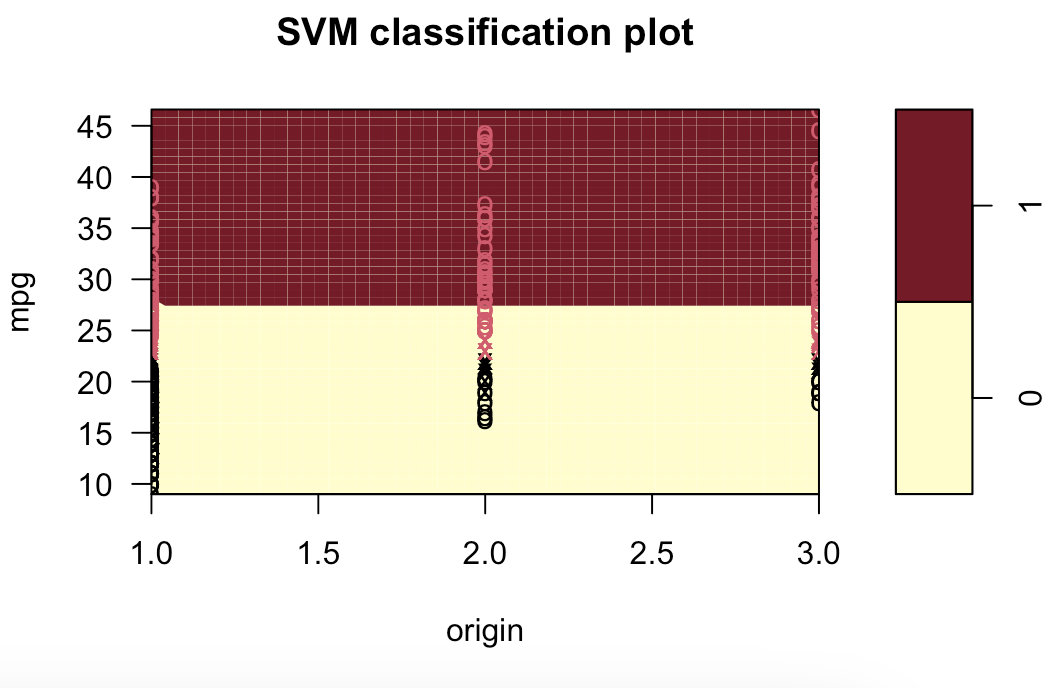
    image-20241107004509480

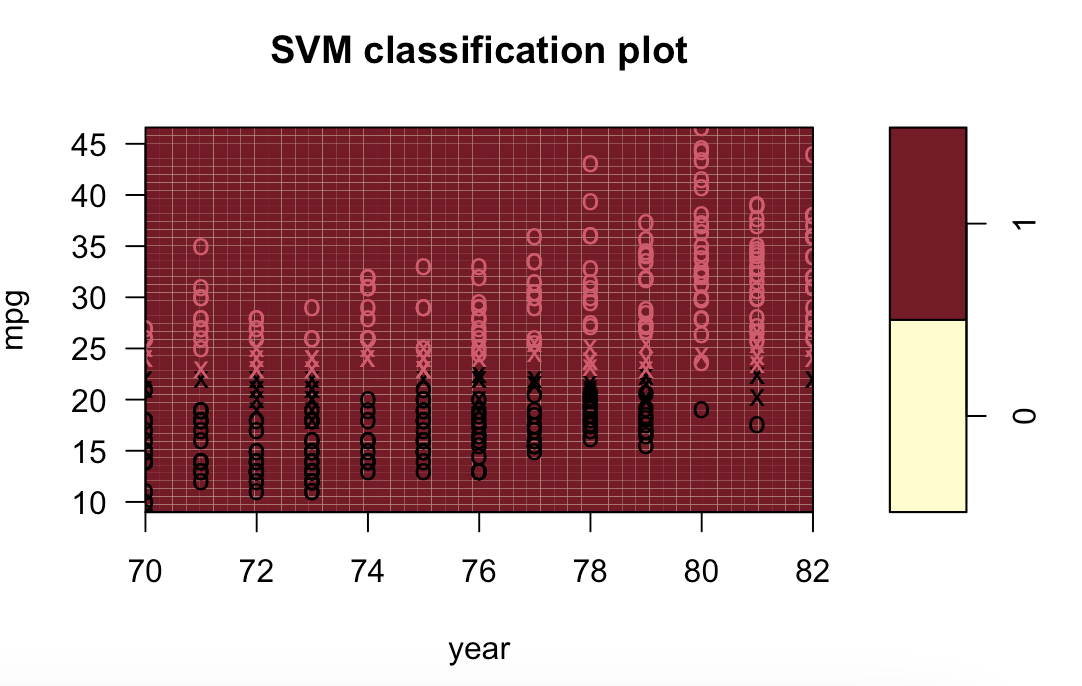
    多项式（列出部分）：

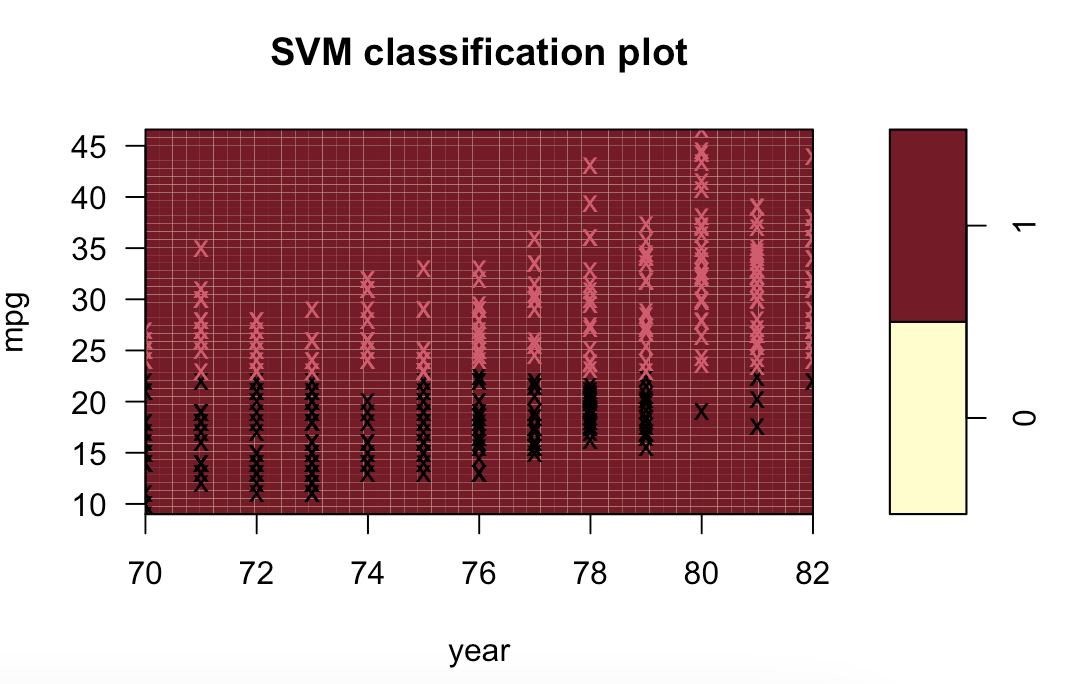
    image-20241107005111424

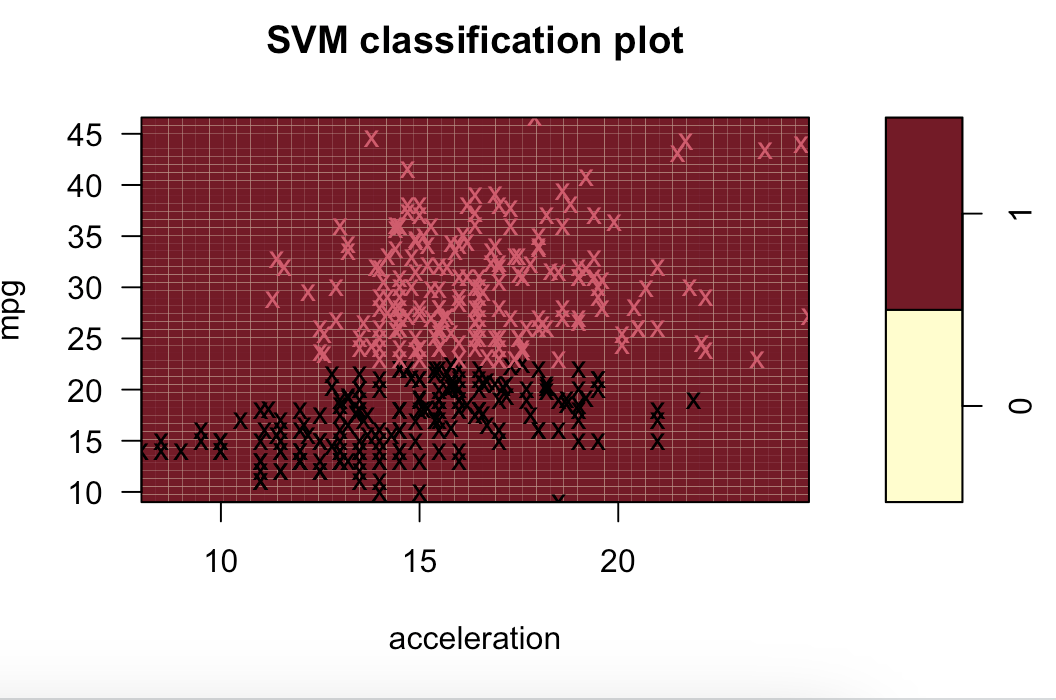
    image-20241107005121794

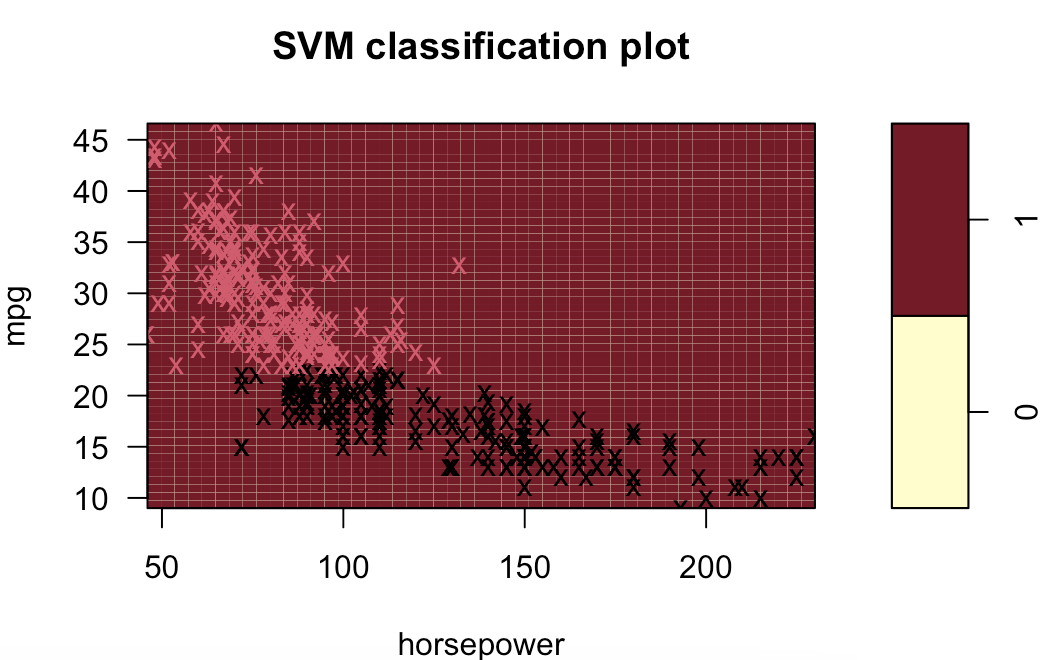
    image-20241107005132608

    径向（列出部分）：

    image-20241107005214077

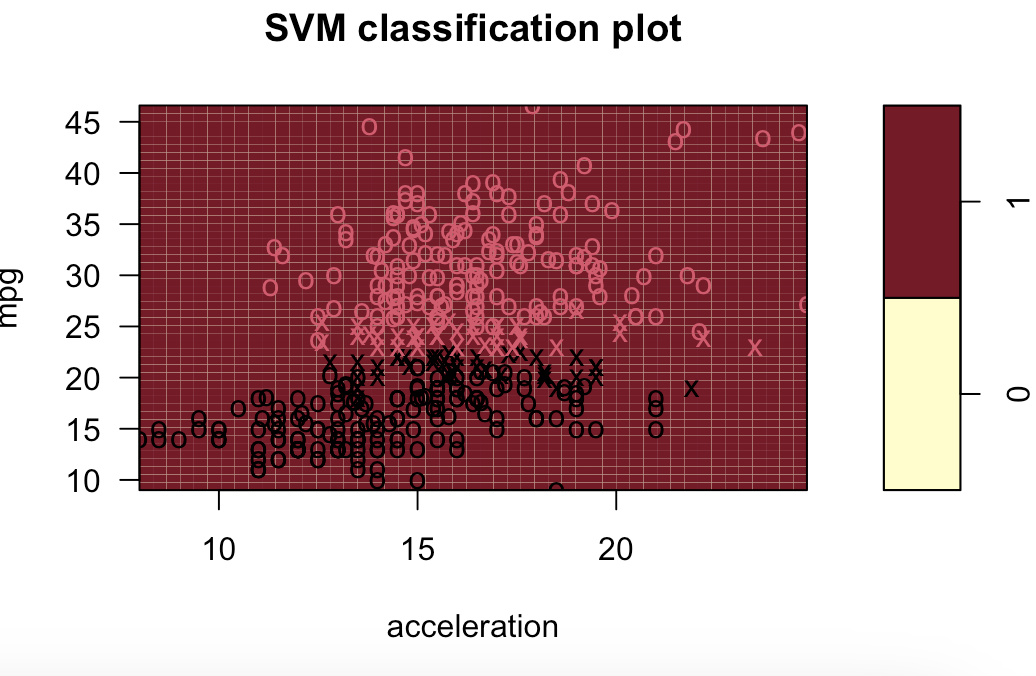
    image-20241107005224658

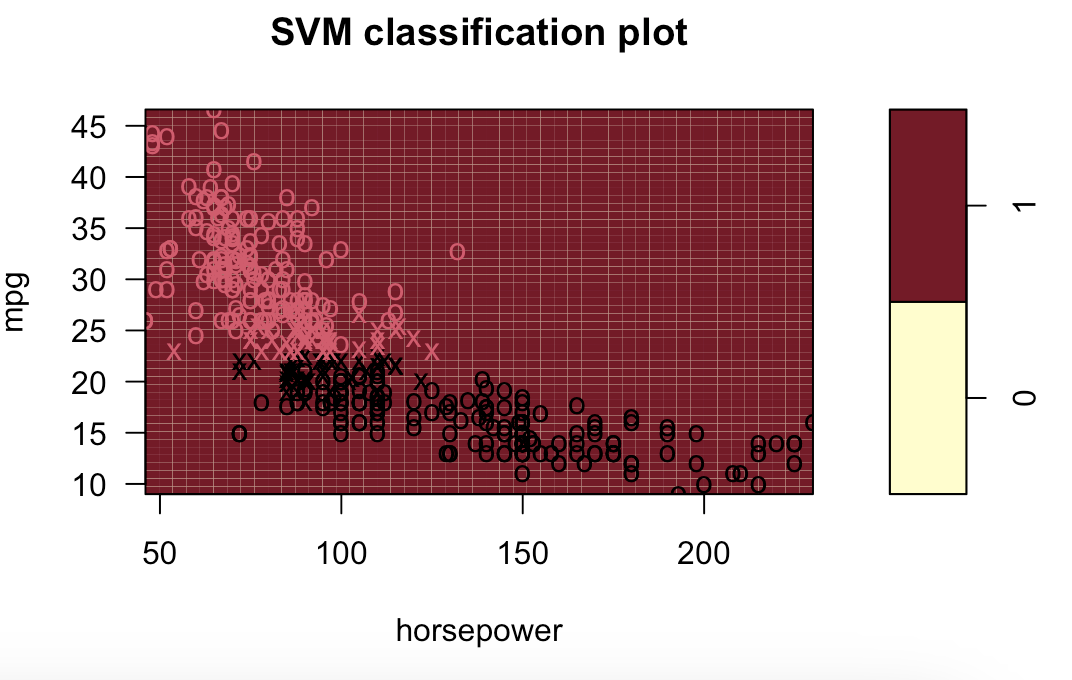
    image-20241107005235769

  • 完整代码

    # 7.(a)
library(ISLR)
gas.med = median(Auto$mpg)
new.var = ifelse(Auto$mpg > gas.med, 1, 0)
Auto$mpglevel = as.factor(new.var)
​
# 7.(b)
library(e1071)
set.seed(3255)
tune.out = tune(svm, mpglevel ~ ., data = Auto, kernel = "linear", ranges = list(cost = c(0.01, 0.1, 1, 5, 10, 100)))
summary(tune.out)
## 从结果可以看出：当采用 10 折交叉验证，当 cost=1 时，error 最小
​
# 7.(c)
### 多项式核函数
set.seed(21)
tune.out = tune(svm, mpglevel ~ ., data = Auto, kernel = "polynomial", ranges = list(cost = c(0.1, 1, 5, 10), degree = c(2, 3, 4)))
summary(tune.out)
## 当 cost=10,degree=2 时，error 最小。
### 径向核函数
set.seed(463)
tune.out = tune(svm, mpglevel ~ ., data = Auto, kernel = "radial", ranges = list(cost = c(0.1, 1, 5, 10), gamma = c(0.01, 0.1, 1, 5, 10, 100)))
summary(tune.out)
## 当 cost=10,gamma=0.01 时，error 最小
​
# 9.(d)
### 线性模型
svm.linear = svm(mpglevel ~ ., data = Auto, kernel = "linear", cost = 1)
svm.poly = svm(mpglevel ~ ., data = Auto, kernel = "polynomial", cost = 10, degree = 2)
svm.radial = svm(mpglevel ~ ., data = Auto, kernel = "radial", cost = 10, gamma = 0.01)
plotpairs = function(fit) {
  for (name in names(Auto)[!(names(Auto) %in% c("mpg", "mpglevel", "name"))]) {
    plot(fit, Auto, as.formula(paste("mpg~", name, sep = "")))
  }
}
plotpairs(svm.linear)
plotpairs(svm.poly)
plotpairs(svm.radial)