本系列内容为《统计学习导论——基于R应用》（机械工业出版社）部分课后习题答案。

本章为2.4节习题答案。

声明：本博客中的习题分享仅供学习和参考之用。请勿将其用于任何形式的学术欺骗、抄袭或违反学术诚信的行为。尊重知识，诚实学习。

如果您发现文章内容中任何不妥或错误之处，请随时通过联系方式或评论功能与我交流，以便我进行改正和完善。

一、概念题

2.4.1

  • (a) 选择光滑度高的模型效果更好。因为光滑度高的模型对样本的拟合效果好（偏差低），但是对预测变量的预测效果差（方差高）。对于样本数大但是预测变量少的情况，光滑度高的模型效果更好。

  • (b) 选择光滑度低的模型效果更好。原因同上，光滑度低的模型对样本拟合效果差（偏差高），但是对预测变量预测效果好（方差低）。对于样本数小但是预测变量多的情况，光滑度低的模型效果更好。

  • (c) 选择光滑度高的模型效果更好。因为光滑度高的模型可以更好拟合预测变量和响应变量的非线性关系，减少欠拟合的风险，而光滑度低的模型更适合线性关系。

  • (d) 选择光滑度低的模型效果更好。因为光滑度高的模型会尝试拟合数据中的更多细节（包含误差、噪声），从而出现过拟合的问题，导致模型对误差过于敏感。而光滑度低的模型更有可能忽略噪声（或者说噪声引起的影响更小），从而保证了拟合的效果。

2.4.3

  • (a)

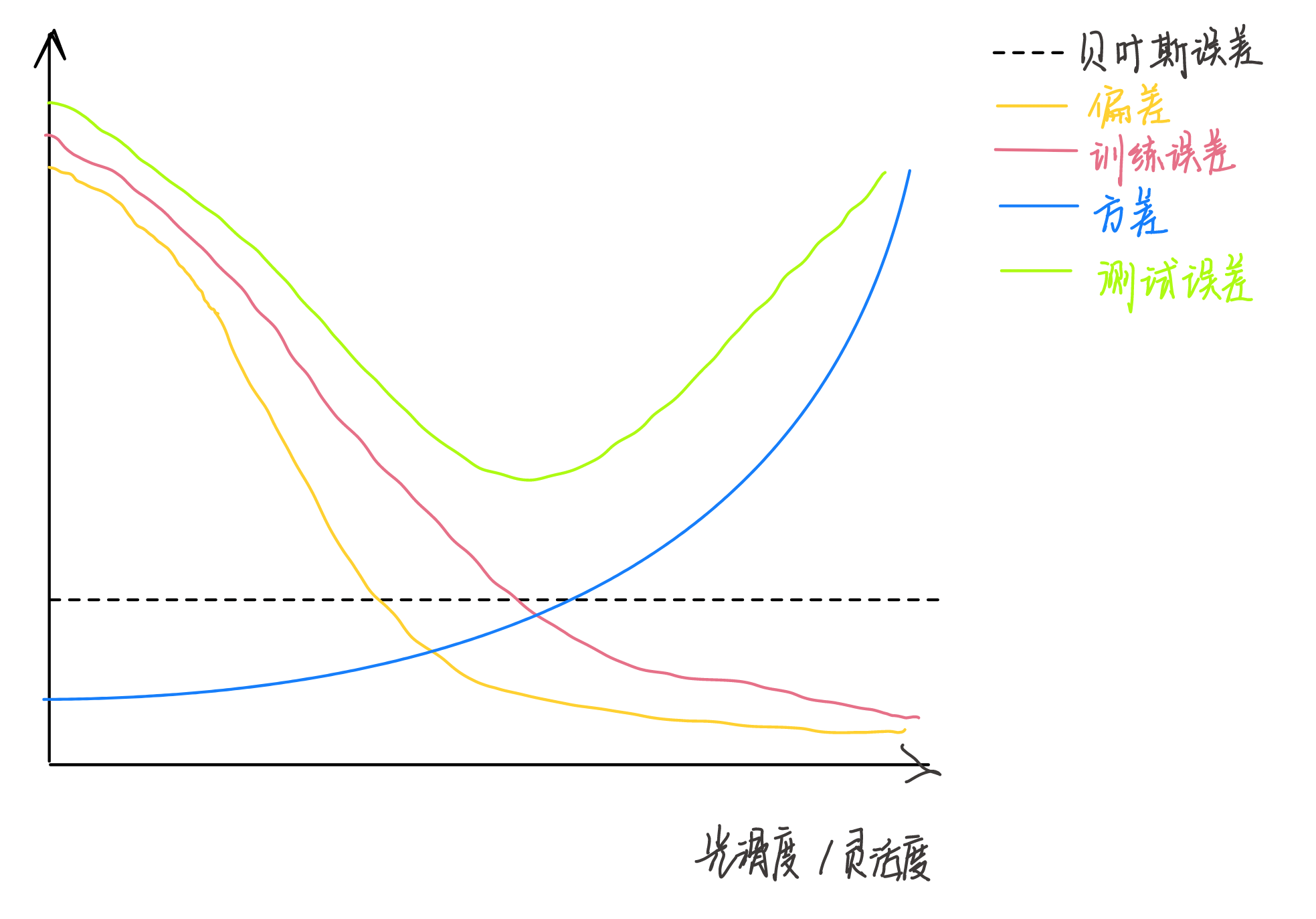
    5be7533e9d4f033dbc2cc95caea6b95b

  • (b)

    • 贝叶斯误差：水平线。贝叶斯（不可约）误差是数据内噪声决定的，不随模型改变而改变。

    • 偏差：单调递减。光滑度越高，模型对样本的拟合效果就越好（虽然可能导致过拟合），而偏差就越小。

    • 训练误差：单调递减。光滑度越高，对样本的拟合训练效果就更好，训练误差越小。

    • 方差：单调递增。随着光滑度（模型复杂度）的增加，模型对训练数据的拟合效果越好，但也更容易对训练数据中的噪声进行拟合。这会导致模型在面对新数据时表现出较高的波动性或不稳定性，因而方差增加。

    • 测试误差：先下降后上升。初始阶段，光滑度的提升会改善模型的拟合效果，测试误差减小。但是，随着光滑度的进一步提升，模型开始过拟合，测试误差增加。

2.4.5

  • 光滑度高的模型：

    • 优点：对样本（训练数据）拟合效果好，偏差以及训练误差低。

    • 缺点：容易出现过拟合，对预测变量（新数据）表现效果差，方差高。同时光滑度高的模型计算复杂度也更高。

    • 适用情况：训练数据噪声（误差）少，样本量较大，更侧重对训练数据的拟合而不是对新变量的预测。

  • 光滑度低的模型：

    • 优点：不容易出现过拟合，对新变量的预测效果相对更好。且模型简单便于训练。

    • 缺点：容易出现欠拟合，对训练数据（样本）拟合效果差，偏差高。

    • 适用情况：训练数据相对较少且噪声较大，更侧重与对新变量的预测而不是对训练数据的拟合。

2.4.6

  • 参数模型：模型结构和参数数量在训练之前就已经确定（例如线性回归中的方程）。

    • 优点：模型计算效率高。模型解释性强。在数据量小的情况下表现效果好。

    • 缺点：不能拟合复杂的数据。模型的选择会直接影响训练效果。在参数模型中需要对数据的分布和关系有严格的假设。

  • 非参数模型：不对模型的形式做假设，参数的数量随数据量变化，复杂度根据数据进行调整（如K-近邻算法、神经网络模型）。

    • 优点：能够拟合复杂数据。适应性强，可以自动调节模型的结构。不需要对数据的分布和关系有严格假设。

    • 缺点：模型计算复杂度高。模型解释性很差。需要很大的数据量来支撑模型的训练。

二、应用题

2.4.8

  • (a)

    # 8.(a)
library(ISLR)
head(College)
write.csv(College, file = "College.csv")
college = read.csv("College.csv")

    image-20240915144044350

  • (b)

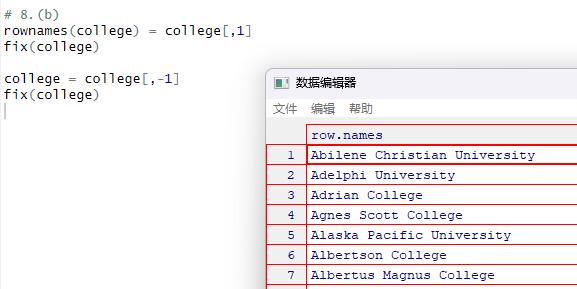
    # 8.(b)
rownames(college) = college[,1]
fix(college)
​
college = college[,-1]
fix(college)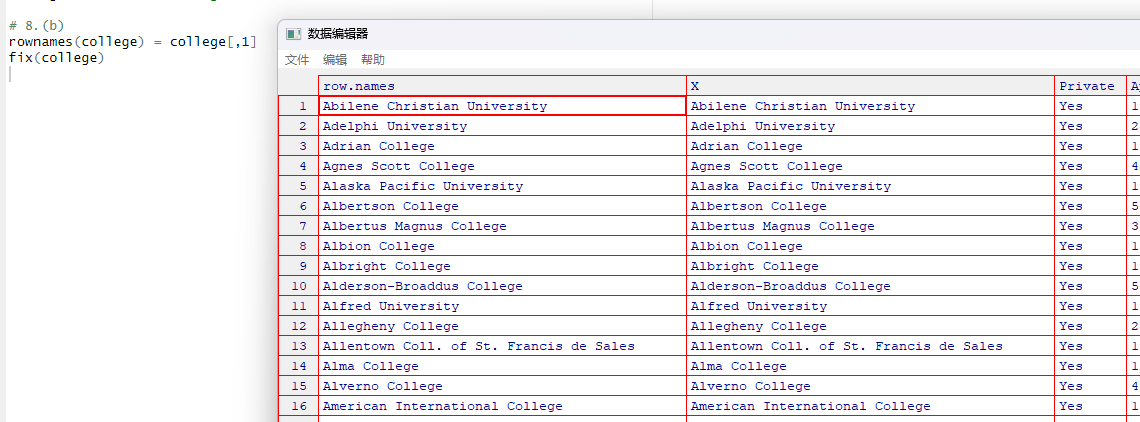

    image-20240915144122800

    image-20240915144223368

  • (c)

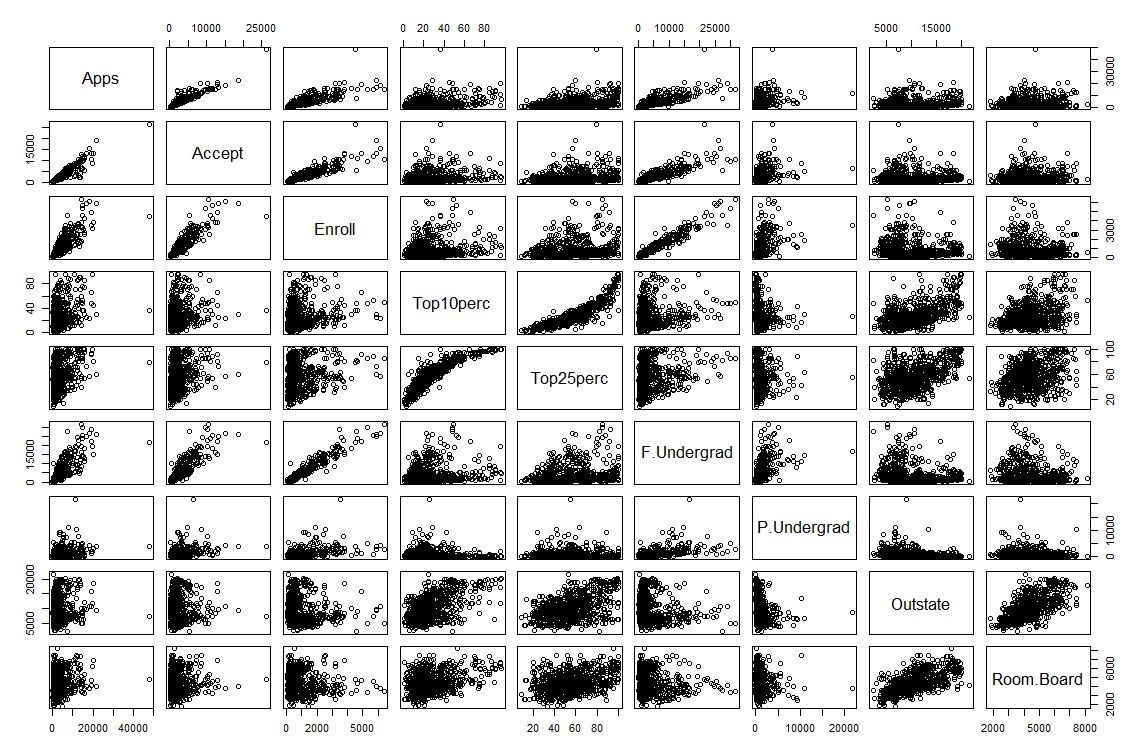
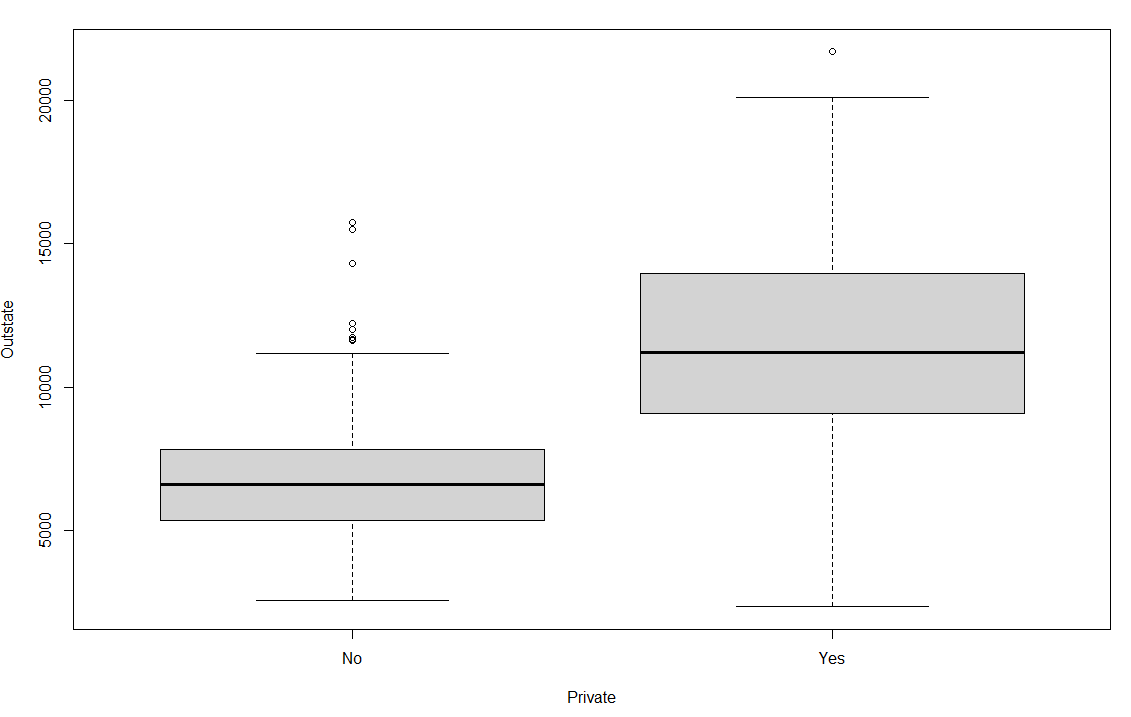
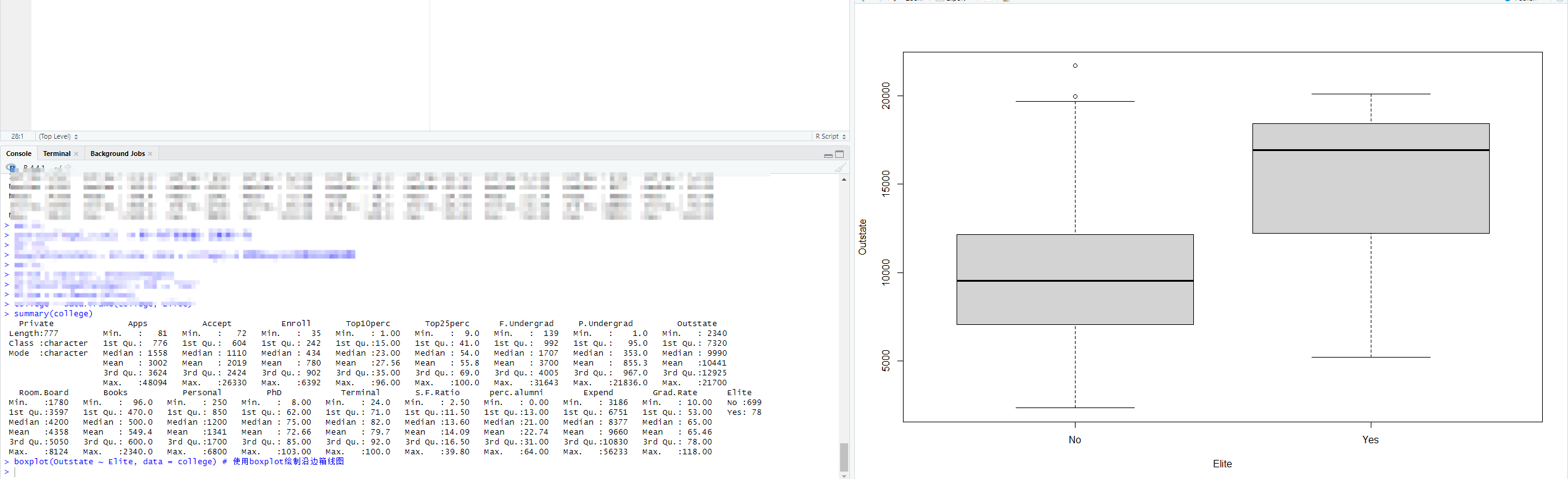
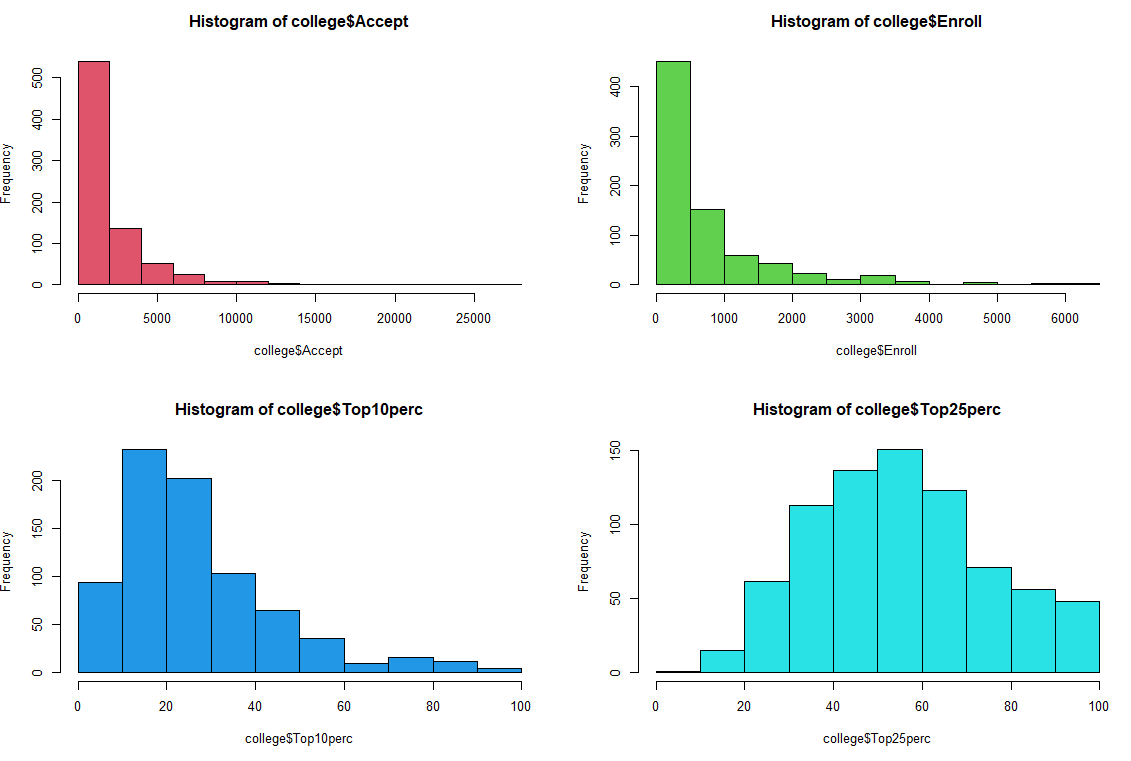
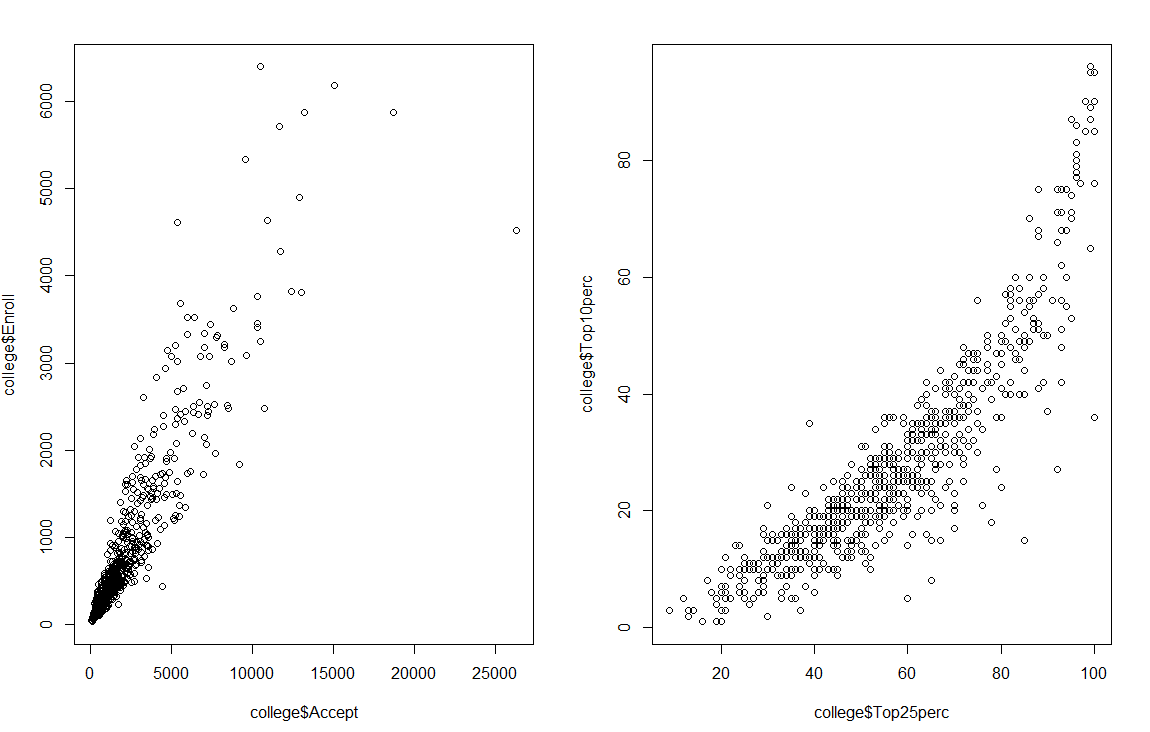
    # 8.(c)
## i.
summary(college)
## ii.
pairs(college[,2:10])  # 第一列不是数量，忽略第一列
## iii.
boxplot(Outstate ~ Private, data = college) # 使用boxplot绘制沿边箱线图
## iv.
Elite = rep("No", nrow(college))
Elite[college$Top10perc > 50] = "Yes"
Elite = as.factor(Elite)
college = data.frame(college, Elite)
summary(college)
boxplot(Outstate ~ Elite, data = college) # 使用boxplot绘制沿边箱线图
## v.
par(mfrow=c(2,2))
hist(college$Accept,col=2)
hist(college$Enroll,col=3)
hist(college$Top10perc,col=4)
hist(college$Top25perc,col=5)
## vi.  注册率随接受率的增长而增长，前10%率随着25%增长增长
par(mfrow=c(1,2))
plot(college$Accept, college$Enroll) # 接受率与注册率
plot(college$Top25perc, college$Top10perc) # 高中前25%与前10%新生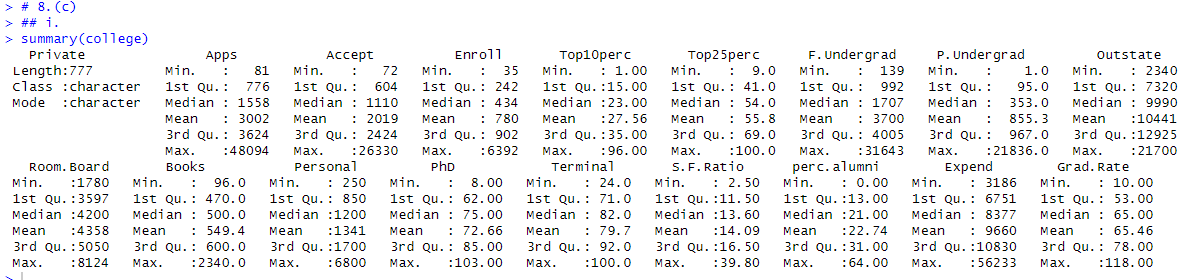

    image-20240915144439717

    image-20240915150027290

    image-20240915150043341

    image-20240915150115247

    image-20240915150345846

    image-20240915150545852

  • 第八题完整代码

    # 8.(a)
library(ISLR)  # 加载ISLR包，该包包含College数据集
head(College)  # 查看College数据集的前几行
write.csv(College, file = "College.csv")  # 将College数据集保存为CSV文件
college = read.csv("College.csv")  # 从CSV文件中读取数据到college变量
​
# 8.(b)
rownames(college) = college[,1]  # 将第一列（学校名称）设置为行名
fix(college)  # 使用数据编辑器检查和修改数据
​
college = college[,-1]  # 删除第一列（学校名称），因为现在已经作为行名了
fix(college)  # 再次使用数据编辑器检查和修改数据
​
# 8.(c)
## i.
summary(college)  # 对college数据集进行总结统计，显示每列数据的基本统计信息
​
## ii.
pairs(college[,2:10])  # 绘制college数据集中第2到第10列的成对散点图矩阵
​
## iii.
boxplot(Outstate ~ Private, data = college)  # 绘制Outstate对Private变量的箱线图，比较私立和公立学校的州外学费
​
## iv.
Elite = rep("No", nrow(college))  # 创建一个新的列Elite，初始值全部为"No"
Elite[college$Top10perc > 50] = "Yes"  # 如果Top10perc值大于50，则将Elite值改为"Yes"
Elite = as.factor(Elite)  # 将Elite列转换为因子类型
college = data.frame(college, Elite)  # 将新的Elite列添加到college数据集中
summary(college)  # 对更新后的college数据集进行总结统计
​
boxplot(Outstate ~ Elite, data = college)  # 绘制Outstate对Elite变量的箱线图，比较精英和非精英学校的州外学费
​
## v.
par(mfrow=c(2,2))  # 设置绘图区域为2x2的布局
hist(college$Accept, col=2)  # 绘制Accept列的直方图，柱状颜色为红色
hist(college$Enroll, col=3)  # 绘制Enroll列的直方图，柱状颜色为绿色
hist(college$Top10perc, col=4)  # 绘制Top10perc列的直方图，柱状颜色为蓝色
hist(college$Top25perc, col=5)  # 绘制Top25perc列的直方图，柱状颜色为洋红色
​
## vi.
# 观察到注册率随接受率的增长而增长，前10%率随着前25%的增长而增长
par(mfrow=c(1,2))  # 设置绘图区域为1x2的布局
plot(college$Accept, college$Enroll)  # 绘制接受率与注册率的散点图
plot(college$Top25perc, college$Top10perc)  # 绘制高中前25%与前10%新生比例的散点图
​

2.4.9

  • (a)

    # 9.(a)
library(ISLR)
auto = Auto # 观察数据集发现origin和name是定性的，其他为定量

  • (b)

    # 9.(b)
sapply(auto[,1:7], range)

    image-20240915151609805

  • (c)

    # 9.(c)
sapply(auto[,1:7], mean)
sapply(auto[,1:7], var)

    image-20240915151740341

  • (d)

    # 9.(d)
auto_2 = auto[-10, ]
auto_2 = auto[-85, ]
sapply(auto_2[,1:7], range)
sapply(auto_2[,1:7], mean)
sapply(auto_2[,1:7], var)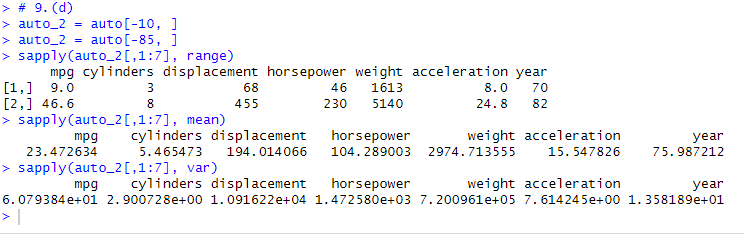

    image-20240915151827808

  • (e)

    # 9.(e)
pairs(auto[,1:7])
# 其中mpg和displacement、horsepower、weight，两两之间互有关系
auto_3 = auto[,1:5]
auto_3 = auto[,-2]
pairs(auto_3)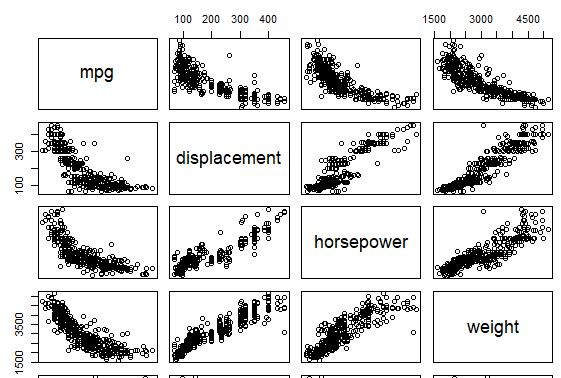

    image-20240915152010213

  • (f)

    # 9.(f)
# 根据9.(e)得到的散点图发现：displacement、horsepower、weight都可以预测mpg

  • 第九题完整代码

    # 9.(a)
library(ISLR)  # 加载ISLR包，该包包含Auto数据集
auto = Auto  # 将Auto数据集赋值给变量auto，方便后续操作
# 观察数据集发现origin和name是定性的，其他为定量
​
# 9.(b)
sapply(auto[,1:7], range)  # 计算auto数据集中前7列（定量变量）的范围（最小值和最大值）
​
# 9.(c)
sapply(auto[,1:7], mean)  # 计算auto数据集中前7列的均值
sapply(auto[,1:7], var)  # 计算auto数据集中前7列的方差
​
# 9.(d)
auto_2 = auto[-10, ]  # 移除第10行的数据
auto_2 = auto[-85, ]  # 移除第85行的数据（这行代码会覆盖掉前一行，应该是'auto_2 = auto_2[-85, ]'）
auto_2 = auto[-c(10, 85), ]  # 正确的移除第10行和第85行的数据
sapply(auto_2[,1:7], range)  # 计算移除两行后数据集中前7列的范围
sapply(auto_2[,1:7], mean)  # 计算移除两行后数据集中前7列的均值
sapply(auto_2[,1:7], var)  # 计算移除两行后数据集中前7列的方差
​
# 9.(e)
pairs(auto[,1:7])  # 绘制auto数据集中前7列变量的成对散点图矩阵
# 其中mpg和displacement、horsepower、weight，两两之间互有关系
auto_3 = auto[,1:5]  # 选择auto数据集中的前5列
auto_3 = auto[,-2]  # 移除auto数据集中的第2列（这行代码会覆盖前一行，应该是'auto_3 = auto_3[,-2]'）
auto_3 = auto[, c(1, 3:7)]  # 完整的选择auto数据集中的第1列和第3到第7列
pairs(auto_3)  # 绘制auto_3数据集的成对散点图矩阵
​
# 9.(f)
# 根据9.(e)得到的散点图发现：displacement、horsepower、weight都可以预测mpg

2.4.10

  • (a)

    # 10.(a)
library(MASS)
Boston
?Boston # 打开帮助文档
dim(Boston) # 506行14列

  • (b)

    # 10.(b)
par(mfrow=c(1,1))
plot(Boston$lstat, Boston$medv) # 低地位人口-自住房价值：观察到低地位人口占比增加，自住房价值中值呈下降趋势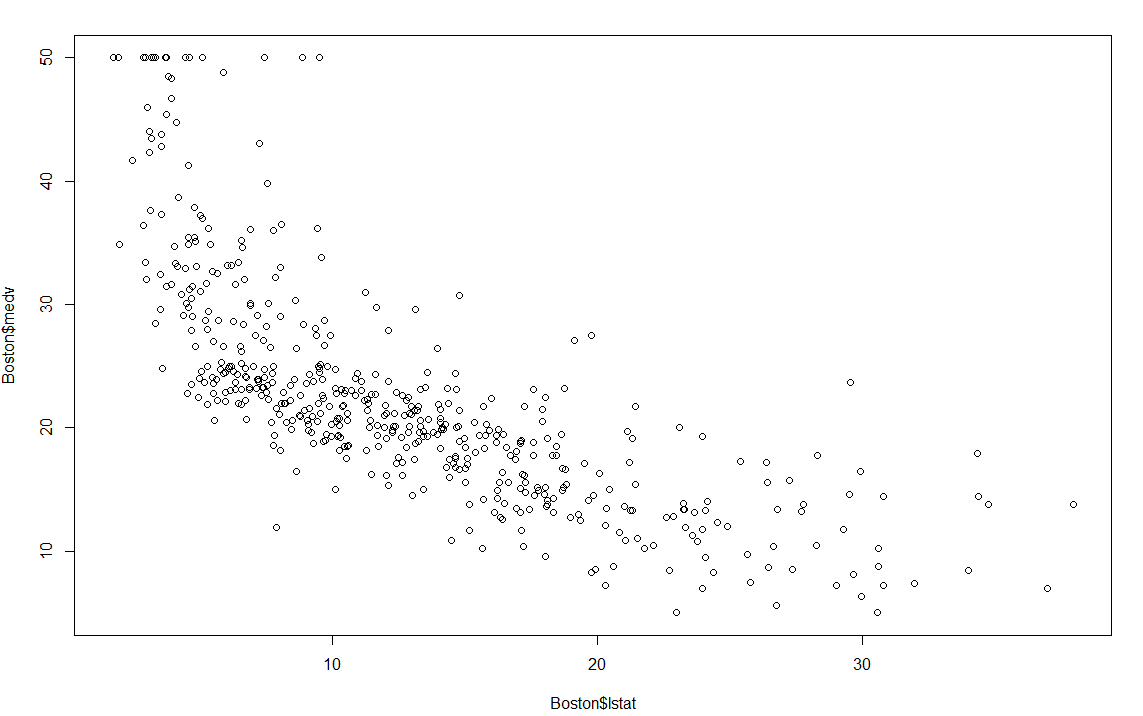

    image-20240915152920948

  • (c)

    # 10.(c)
par(mfrow=c(4, 4))  # 设置绘图区域为4x4的布局，这样可以一次绘制多个散点图
col_names <- names(Boston)  # 获取Boston数据集的列名
for (i in 1:length(col_names)) {  # 循环遍历所有变量，绘制它们与crim的散点图
  plot(Boston[, i], Boston$crim, xlab=col_names[i], ylab="crim", main=paste("crim vs", col_names[i]))  
  # 绘制散点图，x轴为当前变量，y轴为crim，设置合适的标签和标题
}
par(mfrow=c(1, 1))  # 将绘图区域恢复为1x1的布局，以便后续绘图
### 根据结果表明age越大crim越高，dis越近crim越高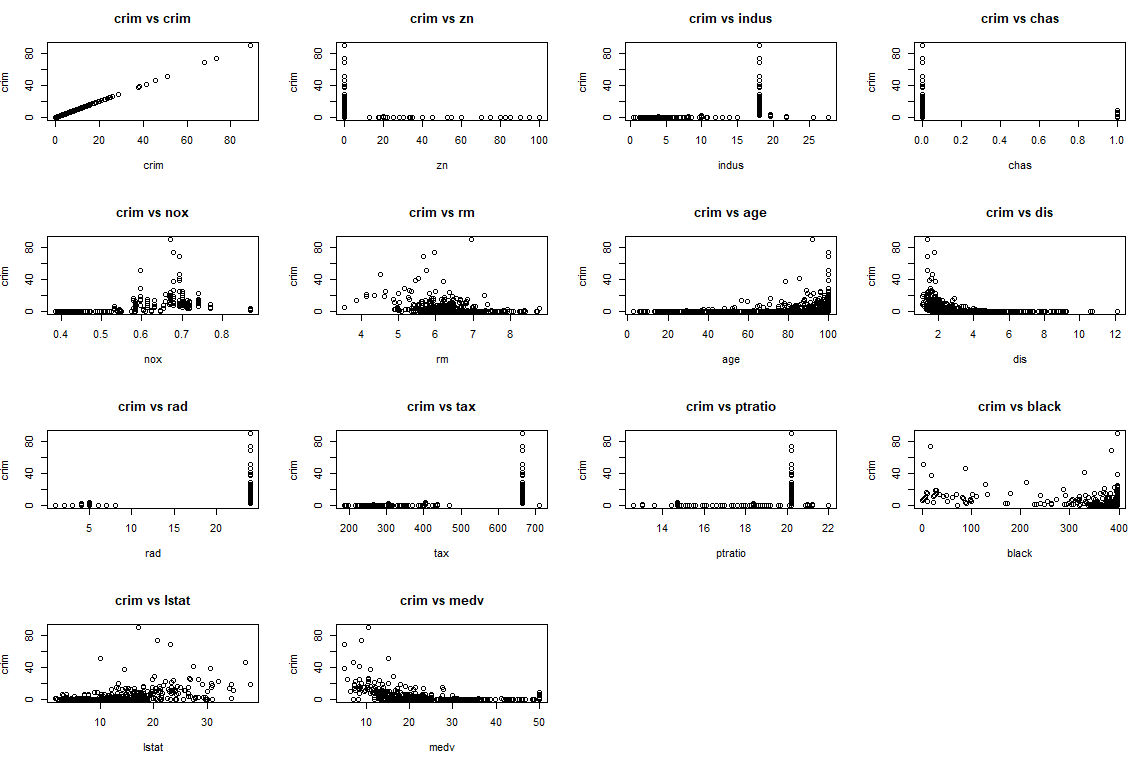

    image-20240915153346387

  • (d)

    # 10.(d)
par(mfrow=c(3, 3))  # 设置绘图区域为3x3的布局
# 犯罪率 (crim) 的直方图
# 大部分城市犯罪率较低（小于20占大多数）
hist(Boston$crim[Boston$crim > 1], breaks=30)  # 犯罪率大于1的直方图
hist(Boston$crim[Boston$crim > 2], breaks=30)  # 犯罪率大于2的直方图
hist(Boston$crim[Boston$crim > 5], breaks=30)  # 犯罪率大于5的直方图
# 税率 (tax) 的直方图
# 大部分城市税率在250-400之间，还有很多一部分城市的税率在660附近
hist(Boston$tax, breaks=30)  # 所有数据的直方图
hist(Boston$tax[Boston$tax > 400], breaks=30)  # 税率大于400的直方图
hist(Boston$tax[Boston$tax > 600], breaks=30)  # 税率大于600的直方图
# 师生比率 (ptratio) 的直方图
# 除了在20左右分布大量数据外，其他师生比率下分布比较均匀
hist(Boston$ptratio, breaks=30)  # 所有数据的直方图
hist(Boston$ptratio[Boston$ptratio > 16], breaks=30)  # 师生比率大于16的直方图
hist(Boston$ptratio[Boston$ptratio > 18], breaks=30)  # 师生比率大于18的直方图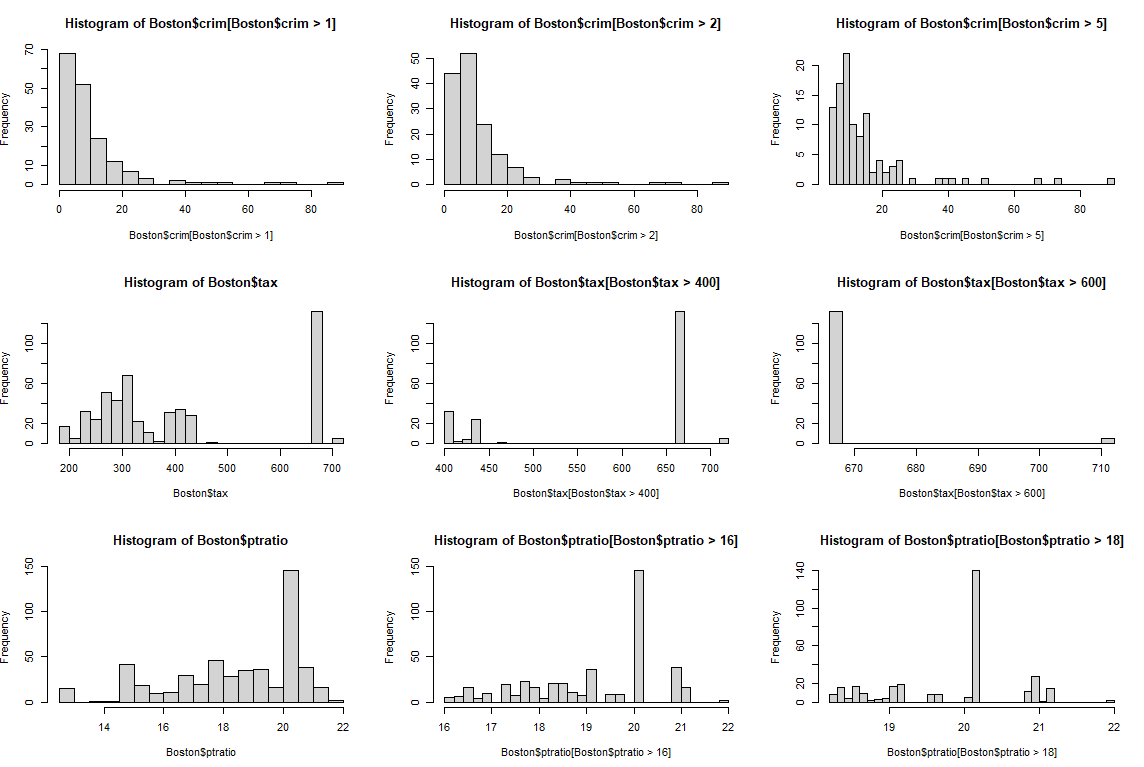

    image-20240915153808624

  • (e)

    # 10.(e) 
num_near_charles = sum(Boston$chas == 1)
num_near_charles # 35个郊区在查尔斯河岸附近

  • (f)

    # 10.(f)
median_ptratio = median(Boston$ptratio)
median_ptratio # 城镇师生比的中位数是19.05

  • (g)

    # 10.(g)
min_medv_index = which.min(Boston$medv)  # 找到业主自用住房中位数最小的郊区
min_medv_suburb = Boston[min_medv_index, ]  # 提取该索引对应的郊区数据
min_medv_suburb  # 输出该郊区的所有变量值
variable_distributions = list()  # 初始化一个用于存储变量值及其分位数的空列表
# 计算该郊区变量在总体分布中的位置
for (variable in names(min_medv_suburb)) {
  if (is.numeric(Boston[[variable]])) {  # 检查变量是否为数值型
    variable_distributions[[variable]] = list(
      value = min_medv_suburb[[variable]],  # 获取该变量在目标郊区的取值
      quantile = ecdf(Boston[[variable]])(min_medv_suburb[[variable]])  # 计算该值在总体分布中的分位数
    )
  }
}
variable_distributions  # 输出每个变量的值和其在总体分布中的位置
### 业主自用住房中位数最小的郊区（medv为5）在多个变量上表现极端，例如高犯罪率、高税收负担、低房间数和高贫困率，反映出该郊区生活环境和经济状况较差。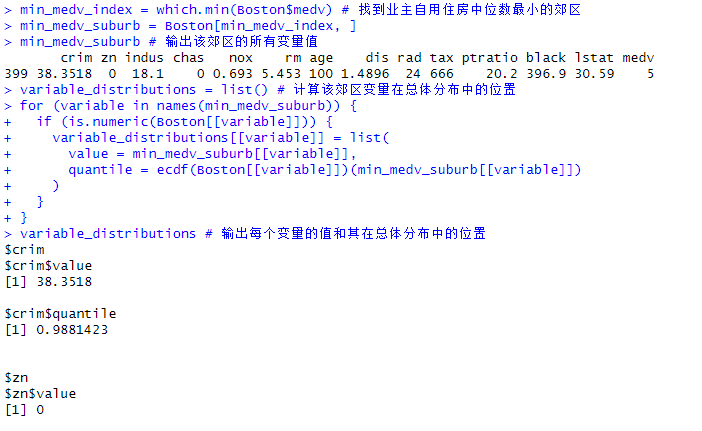

    image-20240915154727550

  • (h)

    # 10.(h)
num_suburbs_rm_over_7 = sum(Boston$rm > 7) # 计算平均居住房间数量超过7的郊区数量
num_suburbs_rm_over_7  # 打印结果
num_suburbs_rm_over_8 = sum(Boston$rm > 8) # 计算平均居住房间数量超过8的郊区数量
num_suburbs_rm_over_8  # 打印结果
suburbs_rm_over_8 = Boston[Boston$rm > 8, ] # 提取平均居住房间数量超过8的郊区数据
summary(suburbs_rm_over_8) # 打印这些郊区的特征
### 平均居住房间数量超过8的郊区特点是犯罪率相对较低，氮氧化物浓度和税收负担较低，房屋较新，且房价普遍较高，显示出这些郊区的生活环境和经济状况较好。
### 尽管其中某些郊区的税率和辐射指数较高，但总体来看，这些郊区的教育资源、住房质量和居民的生活水平都较优越。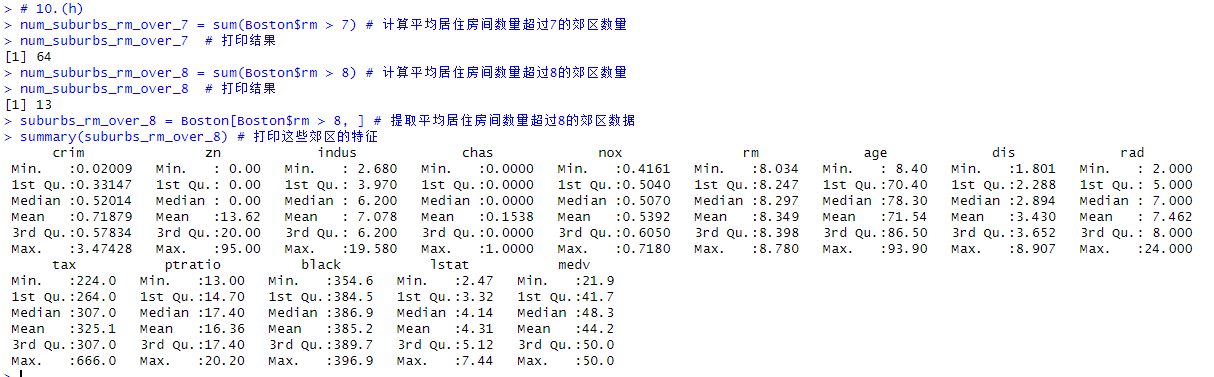

    image-20240915155227380

  • 第十题完整代码

    # 10.(a)
library(MASS)
Boston
?Boston # 打开帮助文档
dim(Boston) # 506行14列
​
# 10.(b)
par(mfrow=c(1,1))
plot(Boston$lstat, Boston$medv) # 低地位人口-自住房价值：观察到低地位人口占比增加，自住房价值中值呈下降趋势
​
# 10.(c)
par(mfrow=c(4, 4))  # 设置绘图区域为4x4的布局，这样可以一次绘制多个散点图
col_names <- names(Boston)  # 获取Boston数据集的列名
for (i in 1:length(col_names)) {  # 循环遍历所有变量，绘制它们与crim的散点图
  plot(Boston[, i], Boston$crim, xlab=col_names[i], ylab="crim", main=paste("crim vs", col_names[i]))  
  # 绘制散点图，x轴为当前变量，y轴为crim，设置合适的标签和标题
}
par(mfrow=c(1, 1))  # 将绘图区域恢复为1x1的布局，以便后续绘图
### 根据结果表明age越大crim越高，dis越近crim越高
​
# 10.(d)
par(mfrow=c(3, 3))  # 设置绘图区域为3x3的布局
# 犯罪率 (crim) 的直方图
# 大部分城市犯罪率较低（小于20占大多数）
hist(Boston$crim[Boston$crim > 1], breaks=30)  # 犯罪率大于1的直方图
hist(Boston$crim[Boston$crim > 2], breaks=30)  # 犯罪率大于2的直方图
hist(Boston$crim[Boston$crim > 5], breaks=30)  # 犯罪率大于5的直方图
# 税率 (tax) 的直方图
# 大部分城市税率在250-400之间，还有很多一部分城市的税率在660附近
hist(Boston$tax, breaks=30)  # 所有数据的直方图
hist(Boston$tax[Boston$tax > 400], breaks=30)  # 税率大于400的直方图
hist(Boston$tax[Boston$tax > 600], breaks=30)  # 税率大于600的直方图
# 师生比率 (ptratio) 的直方图
# 除了在20左右分布大量数据外，其他师生比率下分布比较均匀
hist(Boston$ptratio, breaks=30)  # 所有数据的直方图
hist(Boston$ptratio[Boston$ptratio > 16], breaks=30)  # 师生比率大于16的直方图
hist(Boston$ptratio[Boston$ptratio > 18], breaks=30)  # 师生比率大于18的直方图
​
# 10.(e) 
num_near_charles = sum(Boston$chas == 1)
num_near_charles # 35个郊区在查尔斯河岸附近
​
# 10.(f)
median_ptratio = median(Boston$ptratio)
median_ptratio # 城镇师生比的中位数是19.05
​
# 10.(g)
min_medv_index = which.min(Boston$medv)  # 找到业主自用住房中位数最小的郊区
min_medv_suburb = Boston[min_medv_index, ]  # 提取该索引对应的郊区数据
min_medv_suburb  # 输出该郊区的所有变量值
variable_distributions = list()  # 初始化一个用于存储变量值及其分位数的空列表
# 计算该郊区变量在总体分布中的位置
for (variable in names(min_medv_suburb)) {
  if (is.numeric(Boston[[variable]])) {  # 检查变量是否为数值型
    variable_distributions[[variable]] = list(
      value = min_medv_suburb[[variable]],  # 获取该变量在目标郊区的取值
      quantile = ecdf(Boston[[variable]])(min_medv_suburb[[variable]])  # 计算该值在总体分布中的分位数
    )
  }
}
variable_distributions  # 输出每个变量的值和其在总体分布中的位置
### 业主自用住房中位数最小的郊区（medv为5）在多个变量上表现极端，例如高犯罪率、高税收负担、低房间数和高贫困率，反映出该郊区生活环境和经济状况较差。
​
# 10.(h)
num_suburbs_rm_over_7 = sum(Boston$rm > 7) # 计算平均居住房间数量超过7的郊区数量
num_suburbs_rm_over_7  # 打印结果
num_suburbs_rm_over_8 = sum(Boston$rm > 8) # 计算平均居住房间数量超过8的郊区数量
num_suburbs_rm_over_8  # 打印结果
suburbs_rm_over_8 = Boston[Boston$rm > 8, ] # 提取平均居住房间数量超过8的郊区数据
summary(suburbs_rm_over_8) # 打印这些郊区的特征
### 平均居住房间数量超过8的郊区特点是犯罪率相对较低，氮氧化物浓度和税收负担较低，房屋较新，且房价普遍较高，显示出这些郊区的生活环境和经济状况较好。
### 尽管其中某些郊区的税率和辐射指数较高，但总体来看，这些郊区的教育资源、住房质量和居民的生活水平都较优越。